Лекции 17 Евклидово пространство
Содержание лекции: Евклидово пространство. Ортонормированный базис. Понятие метрического пространства. Метрическое пространство Rn.
Рассмотрим линейное пространство L. Наряду с операциями сложения векторов и умножения вектора на число введем в этом пространстве еще одну операцию – операцию скалярного умножения.
Определение 1
Если каждой паре векторов а, b Î L по некоторому правилу поставить в соответствие действительное число, обозначаемое символом (а, b) и удовлетворяющее условиям
1. (а, b) = (b,а),
2. (а + с, b) = (а, b) + (с, b),
3. (aа, b) = a(а, b)
4. 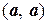 > 0 " а ¹ 0 и
> 0 " а ¹ 0 и 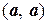 = 0 Û а = 0,
= 0 Û а = 0,
то это правило называется скалярным умножением, а число (а, b) называется скалярным произведением вектора а на вектор b.
Число 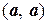 называют скалярным квадратом вектора а и обозначают
называют скалярным квадратом вектора а и обозначают 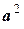 , т. е.
, т. е. 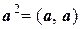 .
.
Условия 1) – 4) называют свойствами скалярного произведения: первое – свойством симметрии (коммутативности), второе и третье – свойствами линейности, четвертое – положительной определенности, а условие 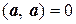 Û
Û 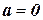 называют условием невырожденности скалярного произведения.
называют условием невырожденности скалярного произведения.
Определение 2
Евклидовым пространством называется действительное линейное пространство, на котором введена операция скалярного умножения векторов.
Евклидово пространство обозначают Е.
Свойства 1) – 4) скалярного произведения при этом называют аксиомами евклидова пространства.
Рассмотрим примеры евклидовых пространств.
· Пространства V2 и V3 являются евклидовыми пространствами, т.к. на них скалярное произведение, удовлетворяющее всем аксиомам, было определено следующим образом
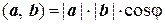 .
.
· В линейном пространстве Rп(x) многочленов степени не выше п скалярное умножение векторов 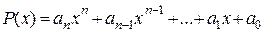 и
и 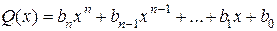 можно ввести по формуле
можно ввести по формуле
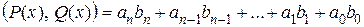 .
.
Проверим выполнение свойств скалярного произведения для введенной операции.
1) 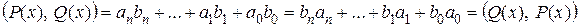 .
.
2) Рассмотрим 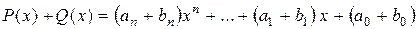 . Пусть
. Пусть 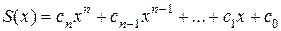 , тогда
, тогда
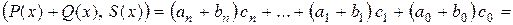
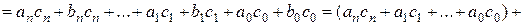
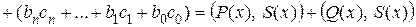 .
.
3) 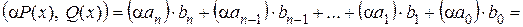
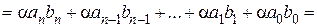
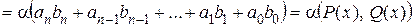 .
.
4)  . Но сумма квадратов любых чисел всегда больше либо равна нулю, причем равна нулю тогда и только тогда, когда все эти числа равны нулю. Следовательно,
. Но сумма квадратов любых чисел всегда больше либо равна нулю, причем равна нулю тогда и только тогда, когда все эти числа равны нулю. Следовательно, 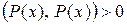 , если многочлен
, если многочлен 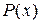 не равен тождественно нулю (т.е. среди его коэффициентов есть отличные от нуля) и
не равен тождественно нулю (т.е. среди его коэффициентов есть отличные от нуля) и 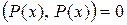 Û когда
Û когда 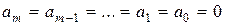 , что означает
, что означает 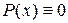 .
.
Таким образом, все свойства скалярного произведения выполняются, значит, равенство 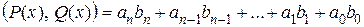 определяет скалярное умножение векторов пространства Rп(x), а само это пространство является евклидовым.
определяет скалярное умножение векторов пространства Rп(x), а само это пространство является евклидовым.
· В линейном пространстве Rn скалярное умножение вектора 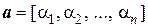 на вектор
на вектор 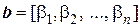 может быть определено по формуле
может быть определено по формуле
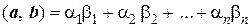 .
.
Покажем, что в любом линейном пространстве может быть определено скалярное умножение, т.е. любое линейное пространство можно сделать евклидовым пространством. Для этого возьмем в пространстве Ln произвольный базис {а1, а2, …, ап}. Пусть в этом базисе
а = a1а1+ a2 а2+ …+ aпап и b = b1а1 + b2а2 + …+ bпап.
Положим
(а, b) = a1b1+ a2b2+ …+ aпbп. (*)
Проверим выполнение свойств скалярного произведения:
1) (а, b) = a1b1+ a2b2+ …+ aпbп = b1a1+ b2a2+ …+bпaп= (b, а),
2) Если 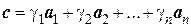 ,то
,то
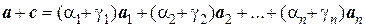 .
.
Тогда
(а + с, b) = 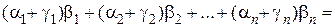
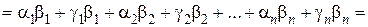
= 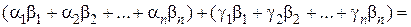 (а, b) + (с, b).
(а, b) + (с, b).
3. (lа, b) = (la1)b1+ (la2)b2+ …+ (laп)bп = la1b1 + la2b2 + …+ laпbп =
= l(a1b1) + l(a2b2) + …+ l(aпbп) = l (а, b).
4. 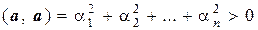 " а ¹ 0 и
" а ¹ 0 и 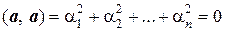 тогда и только тогда, когда все ai = 0, т.е. а = 0.
тогда и только тогда, когда все ai = 0, т.е. а = 0.
Следовательно, равенство (а, b) = a1b1 + a2b2 + …+ aпbп определяет в Ln скалярное произведение.
Заметим, что рассмотренное равенство (а, b) = a1b1+ a2b2+ …+ aпbп для различных базисов пространства дает различные значения скалярного произведения одних и тех же векторов а и b. Более того, скалярное произведение может быть определено и каким-либо принципиально другим способом. Поэтому будем называть задание скалярного произведения с помощью равенства (*) традиционным.
Определение 3
Нормойвектораа евклидова пространства называется арифметическое значение квадратного корня из скалярного квадрата этого вектора.
Норму вектора обозначают ||а||, или [а], или | а |. Итак, то определению,
||а|| 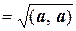 .
.
Имеют место следующие свойства нормы:
1. ||а|| = 0 Û а =0.
2. ||aа||= |a|.||а|| "a ÎR.
3. |(а, b)| £ ||а||.||b|| (неравенство Коши - Буняковского).
4. ||а+b|| £ ||а|| + ||b|| (неравенство треугольника).
В евклидовых пространствах V2 и V3 с традиционным образом заданным скалярным умножением норма вектора `а есть его длина
||`а || = |`а |.
В евклидовом пространстве Rn со скалярным умножением 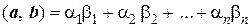 норма вектора
норма вектора 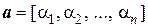 равна
равна
|| a || = 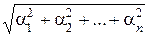 .
.
Определение 4
Вектор а евклидова пространства называется нормированным(или единичным), если его норма равна единице: || a|| = 1.
Если а¹ 0, то векторы 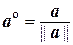 и
и 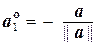 – единичные векторы. Нахождение для заданного вектора асоответствующего ему единичного вектора
– единичные векторы. Нахождение для заданного вектора асоответствующего ему единичного вектора 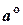 (или
(или 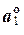 ) называется нормированием вектора а.
) называется нормированием вектора а.
Из неравенства Коши – Буняковского следует, что
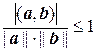 , откуда
, откуда 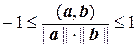 ,
,
поэтому отношение 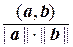 можно рассматривать как косинус некоторого угла.
можно рассматривать как косинус некоторого угла.
Определение 5
Угол j (0£ j <p), для которого cosj = 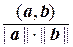 , называется углом между векторами а и b евклидова пространства.
, называется углом между векторами а и b евклидова пространства.
Таким образом, угол между векторами а и b евклидова пространства определяется по формуле
j = 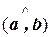 = arccos
= arccos 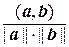 .
.
Заметим, что введение скалярного умножения в линейном пространстве дает возможность производить в этом пространстве «измерения», подобные тем, которые возможны в пространстве геометрических векторов, а именно измерение «длин» векторов и «углов» между векторами, при этом выбор формы задания скалярного умножения аналогичен выбору «масштаба» для таких измерений. Это позволяет распространить на произвольные линейные пространства методы геометрии, связанные с измерениями, тем самым значительно усилив средства исследования математических объектов, встречающихся в алгебре и анализе.
Определение 6
Векторы а и b евклидова пространства называются ортогональными, если их скалярное произведение равно нулю:
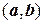 = 0.
= 0.
Заметим, что если хотя бы один из векторов нулевой, то равенство 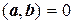 выполняется. Действительно, т.к. нулевой вектор можно представить в виде 0 = 0.а, то (0, b) = (0.а, b) = 0.(а, b) = 0. Следовательно, нулевой вектор ортогонален к любому вектору евклидова пространства.
выполняется. Действительно, т.к. нулевой вектор можно представить в виде 0 = 0.а, то (0, b) = (0.а, b) = 0.(а, b) = 0. Следовательно, нулевой вектор ортогонален к любому вектору евклидова пространства.
Определение 7
Система векторов а1, а2, …, ат евклидова пространства называется ортогональной, если эти векторы попарно ортогональны, т.е.
(аi, аj) = 0 "i ¹ j, i, j =1,2,…,m.
Система векторов а1, а2, …, ат евклидова пространства называется ортонормированной (или ортонормальной), если она ортогональная и каждый ее вектор – нормированный, т.е.
(аi, аj) = 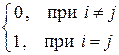 , i, j = 1,2, …, m.
, i, j = 1,2, …, m.
Ортогональная система векторов обладает свойствами:
1. Если 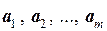 – ортогональная система ненулевых векторов, то система
– ортогональная система ненулевых векторов, то система 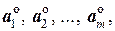 полученная нормированием каждого из векторов данной системы, также является ортогональной.
полученная нормированием каждого из векторов данной системы, также является ортогональной.
2. Ортогональная система ненулевых векторов линейно независима.
Если всякая ортогональная, а значит, и ортонормированная система векторов линейно независима, то может ли такая система образовывать базис заданного пространства? На этот вопрос отвечает следующая теорема.
Теорема 3
Во всяком п-мерном евклидовом пространстве ( 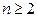 ) существует ортонормированный базис.
) существует ортонормированный базис.
Доказательство
Доказать теорему – значит найти этот базис. Поэтому поступим следующим образом.
Рассмотрим в заданном евклидовом пространстве произвольный базис {а1, а2, …, аn}, по нему построим ортогональный базис {g1, g2, …, gn}, а затем нормируем векторы этого базиса, т.е. положим 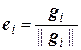 . Тогда система векторов {е1, е2,…, еn} образует ортонормированный базис.
. Тогда система векторов {е1, е2,…, еn} образует ортонормированный базис.
Итак, пусть Б:{а1, а2, …, аn} – произвольный базис рассматриваемого пространства.
1. Положим
g1 = а1, g2 = а2 + 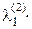 g1
g1
и подберем коэффициент 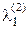 так, чтобы вектор g2 был ортогонален вектору g1, т.е. (g1, g2) = 0. Поскольку
так, чтобы вектор g2 был ортогонален вектору g1, т.е. (g1, g2) = 0. Поскольку
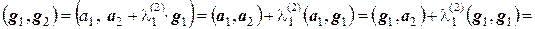
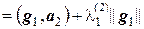 ,
,
то из равенства 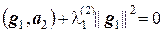 находим
находим 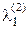 = –
= – 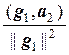 .
.
Тогда вектор g2 = а2 – 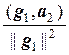 g1 ортогонален вектору g1.
g1 ортогонален вектору g1.
Далее положим
g3 = а3 + 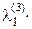 g1 +
g1 + 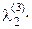 g2 ,
g2 ,
и подберем 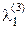 и
и 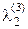 так, чтобы вектор g3 был ортогонален и g2, и g3, т.е. (g1, g3) = 0 и (g2, g3) = 0. Находим
так, чтобы вектор g3 был ортогонален и g2, и g3, т.е. (g1, g3) = 0 и (g2, g3) = 0. Находим
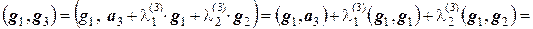
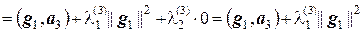 ,
,
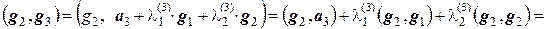
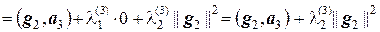 .
.
Тогда из равенств 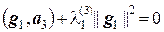 и
и 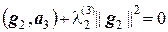 находим соответственно
находим соответственно 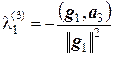 и
и 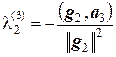 .
.
Таким образом, вектор g3 = а3 –` 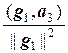 g1 –
g1 – 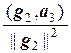 g2 ортогонален векторам g1 и g2.
g2 ортогонален векторам g1 и g2.
Аналогично построим вектор
g4 = а4 –` 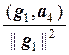 g1 –
g1 – 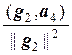 g2 –
g2 – 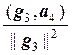 g3.
g3.
Нетрудно проверить, что (g1, g4) = 0, (g2, g4) = 0, (g3, g4) = 0.
Действую далее подобным образом, получим
gп = ап – 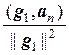 g1 –
g1 – 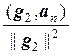 g2 – … –
g2 – … – 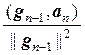 gп–1,
gп–1,
причем этот вектор, в силу взаимной ортогональности векторов g1, g2, …, gп–1, будет ортогонален каждому из этих векторов.
Таким образом, система векторов { g1, g2, …, gп}, где
g1 = а1,
gk = аk – 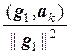 g1 –
g1 – 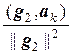 g2 – … –
g2 – … – 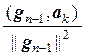 gk–1, k = 2, 3, …, n,
gk–1, k = 2, 3, …, n,
образует ортогональную систему векторов, которая, согласно теореме 5.2, линейно независима, и, следовательно, образует ортогональный базис п-мерного евклидова пространства.
2. Положим теперь 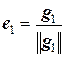 ,
, 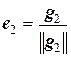 ,
, 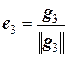 , …,
, …, 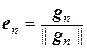 . В силу теорем 5.1 и 5.2, векторы е1, е2, …, еn попарно ортогональны и линейно независимы, а значит, образуют ортонормированный базис рассматриваемого пространства.
. В силу теорем 5.1 и 5.2, векторы е1, е2, …, еn попарно ортогональны и линейно независимы, а значит, образуют ортонормированный базис рассматриваемого пространства.
Таким образом, во всяком евклидовом пространстве существует ортонормированный базис. ▲
Из доказательства этой теоремы следует алгоритм построения ортонормированного базиса (процесс ортогонализации):
1) Взять произвольный базис заданного евклидова пространства.
2) Найти векторы ортогонального базиса по формулам
g1 = а1,
gk = аk – 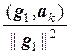 g1 –
g1 – 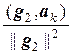 g2 – … –
g2 – … – 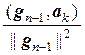 gk–1, k = 2, 3, …, n.
gk–1, k = 2, 3, …, n.
3) Нормировать полученную систему векторов {g1, g2, …, gп}, т.е. положить 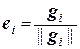 .
.
4) Записать ортонормированный базис {е1, е2, …, еn}.
В дальнейшем ортонормированный базис будем обозначать
Б0:{е1, е2, …, еn}.
Отметим следующие свойства ортонормированного базиса.
1) В ортонормированном базисе скалярное произведение любых двух векторов пространства равно сумме произведений их соответствующих координат: (а, b) = a1b1 + a2b2 + …+ aп bп.
2) Если в некотором базисе скалярное произведение двух векторов равно сумме произведений их соответствующих координат, то этот базис – ортонормированный.
Таким образом, всякий базис евклидова пространства будет ортонормированным, если скалярное произведение определено как сумма произведений координат векторов в этом базисе.
3) В ортонормированном базисе норма вектора равна корню квадратному из суммы квадратов его координат.
|| a || 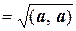 =
= 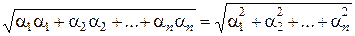 .
.
Определение 8.
Множество М называется метрическим пространством, если существует правило, по которому любым двум его элементам х и у поставлено в соответствие некоторое действительное число r(х,у) называемое расстоянием между этими элементами, удовлетворяющее условиям:
1. r(х,у) = r(у,х);
2. r(х,у)³0 для любых х и у, причем r(х,у)=0 тогда и только тогда, когда х = у;
3. r(х,у) £ r(х, z) + r(у, z) для любых трех элементов х, у, zÎМ.
Элементы метрического пространства называются точками.
Примером метрического пространства является пространство Rn, в нем расстояние между точками (векторами этого пространства) может быть определено по формуле r(х,у) = || х – у ||.
Дата добавления: 2017-11-21; просмотров: 2272;











