Столкновения частиц в плазме

Проанализируем общую картину движения электронов и ионов в плазме при отсутствии внешних полей. Характер этого движения определяется законами взаимодействия частиц. В плазме с высокой степенью ионизации основная форма взаимодействия частиц — рассеяние в кулоновском поле. Нужно различать три основных типа элементарных актов рассеяния: рассеяние электронов на ионах, электронов на электронах и ионов на ионах. Другие элементарные процессы происходят либо с излучением фотонов, либо в них участвуют также и нейтральные частицы (и тогда они отступают на задний план по мере повышения степени ионизации). Примером процессов первого рода может служить испускание тормозного излучения при лонных столкновениях, примером второго — процессы ионизации и возбуждения атомов электронным ударом и явления перезарядки ионов на атомах. Если рассматривается неводородная плазма, то в общем случае следует учитывать взаимодействие электронов с ионами, находящимися в различных энергетических состояниях. В этом случае интенсивность излучения возбужденных ионов может оказаться очень большой, она будет играть заметную роль в энергетическом балансе плазменных процессов.

Мы ограничимся, в основном, анализом взаимодействия частиц в полностью ионизованной плазме.

Пусть через плазму проходит некоторая «пробная» частица (в качестве таковой ямы можем выбрать любой электрон или ион плазмы, зафиксировав внимание на его траектории). Эта заряженная частица испытывает акты рассеяния на своем пути. Если речь идет о движении легкой частицы среди совокупности тяжелых частиц (электрона среди ионов), то центры рассеяния можно считать неподвижными. В указанном случае вероятность рассеяния на тот или иной угол определяется классической формулой Резерфорда.

Каждый акт рассеяния, обусловленный пролетом пробной частицы мимо рассеивающего центра, приводит к повороту траектории частицы на некоторый угол θ , т. е. к уменьшению скорости по первоначальному направлению движения от v до vcosθ . В подавляющем большинстве случаев акты рассеяния происходят на дальних дистанциях, т. е. при больших расстояниях, и, следовательно, как правило, сопровождаются очень малым изменением направления траектории (характерная особенность резерфордовского рассеяния в электрическом поле точечных зарядов!). Поэтому привычная для кинетической теории газов изломанная траектория частицы, состоящая из отдельных прямолинейных участков — пробегов, которые соединяют места «столкновений», в данном случае не имеет смысла. Вместо этого появляется картина плавно извивающейся линии, направление ее изменяется под действием многочисленных, но вместе с тем очень слабых импульсов, обусловленных «столкновениями» с другими частицами. Фактически эти импульсы сливаются в непрерывный ряд воздействий, оказываемых на движущуюся частицу «микрополем» плазмы, образуемым суперпозицией электрических полей отдельных частиц.

В рассматриваемом случае естественно ввести понятие о длине свободного пробега 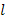как о расстоянии, на протяжении которого частица сохраняет первоначальное направление своей скорости. Это определение соответствует следующему равенству:

.

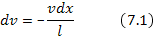Здесь 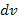— среднее изменение компоненты скорости по первоначальному направлению движения при прохождении отрезка пути dx. С учетом 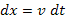(7.1) можно переписать в виде уравнения движения с некоторой эффективной силой трения:

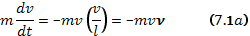
где введенную таким образом величину 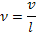называют частотой столкновений.

Пользуясь определением (1.8а), можно представить l с помощью интеграла по угловому распределению рассеянных частиц. Если вектор скорости поворачивается при столкновении на угол θ , то проекция скорости по первоначальному направлению движения уменьшается на величину 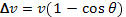. Поскольку основную роль играют акты рассеяния на малые углы 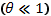, то изменение скорости при элементарном столкновении можно представить как 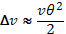. Суммарное изменение скорости за рассеяния на нескольких центрах 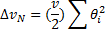, где суммирование проводится по всем N рассеивающим центрам. При прохождении элементарного отрезка пути dx заряженная частица встретится с 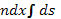рассеивающими центрами, находящимися на всевозможных прицельных расстояниях. Поэтому элемент площади ds можно выразить с помощью прицельного расстояния b как 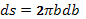, тем более что элементарный угол рассеяния θ зависит именно от b. 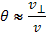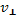Для малых углов рассеяния θ справедливо соотношение , где можно найти с помощью компоненты уравнения движения, перпендикулярной к направлению начальной скорости:

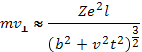
Здесь мы предположили, что траектория пробной частицы представляет собой почти прямую линию, а расстояние наибольшего сближения практически совпадает с прицельным параметром. Отсюда

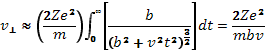
т. е. 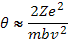. Следовательно, средняя величина

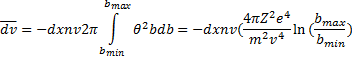(7.2)

Сравнивая (7.2) с формулой (7.1), получаем

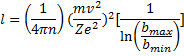(7.3)

Величины 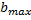, 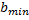оценим исходя из следующих соображений. Электрическое поле рассеивающего центра можно считать кулоновским только на расстояниях, меньших дебаевского радиуса 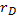. На больших расстояниях оно убывает экспоненциально, и, следовательно, столкновения, при которых частица проходит мимо рассеивающего центра на расстояниях, превышающих 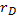, нужно из рассмотрения исключить. В действительности, конечно, дебаевское облако вокруг движущегося заряда лишь в грубом приближении можно считать сферическим. Время релаксации — установления такого облака — имеет тот же порядок величины, что и время пролета зарядом со средней тепловой скоростью расстояния, сравнимого с радиусом облака. Но строгая теория приводит лишь к небольшому количественному уточнению окончательного выражения для длины свободного пробега. Поэтому при вычислении l используем указанный метод обрезания предельного параметра 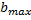на величине 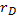. В качестве 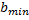можно взять прицельное расстояние, отвечающее рассеянию на углы 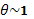, при которых нарушилось бы приближение малых углов.

Полагая 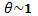, находим

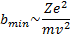(7.4)

Поскольку стоящая под знаком логарифма в (7.3) величина, которая получена таким образом для актов взаимодействия частиц в плазме, оказывается очень большой (во всех представляющих интерес случаях от 10⁴ до 10⁸), то приблизительность оценки b_max и b_min практически не отражается на точности вычисления l. Предположения, при которых найдено выражение для длины свободного пробега l, выполняются в случае, когда пробной частицей является электрон и рассматривается его взаимодействие с ионами плазмы. Среднюю длину свободного пробега, соответствующую ионным столкновениям в плазме, обозначим 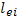. Ее получают при усреднении выражения (7.3) по энергетическому спектру электронов. Если все ионы в плазме имеют единичный заряд, то, предполагая максвелловское распределение электронов по энергиям, получаем следующее выражение для средней длины свободного пробега:

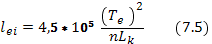
где Т_е — температура электронов, К; L_k —так называемый кулоновский логарифм. Он получается при подстановке в выражение 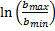значени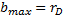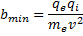й
, и 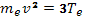, s New Roman" w:h-ansi="Times New Roman"/><wx:font wx:val="Times New Roman"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>-</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>e</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 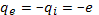. 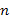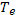В очень широких пределах изменения и логарифм 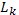изменяется от 10 до 20. Поскольку в физике плазмы часто достаточно даже довольно грубой оценки величин, характеризующих процессы столкновений между частицами, то в дальнейшем будем считать L_k=15.

Кроме 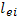можно ввести также некоторые другие усредненные характеристики процессов столкновения между электронами и ионами. Эффективное сечение для таких столкновений определяется соотношением 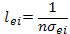, среднее время между двумя соударениями 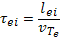где 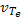— средняя тепловая скорость электронов. Частота столкновений 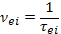. Указанные величины можно вычислить по следующим формулам:

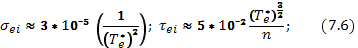(7.6)

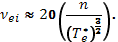
Выражения для всех указанных параметров нетрудно обобщить на случай, когда столкновения происходят с многозарядными ионами. Эффективное сечение 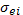возрастет в этом случае пропорционально квадрату заряда иона, соответственно изменятся и остальные величины. Среди различных видов взаимодействия частиц в плазме столкновения между электронами и ионами играют наиболее важную роль, определяя, в частности, механизм таких процессов, как протекание электрического тока и диффузию. Для полной характеристики кулоновского взаимодействия частиц в плазме нужно ввести такие же параметры, характеризующие статистический эффект столкновений между идентичными частицами электрон - электронные и ион-ионные столкновения). В этом случае расчет осложняется тем, что при анализе элементарных актов столкновения нужно учитывать движение рассеивающих центров. Однако очевидно, что учет эффекта может отразиться только на значении численного коэффициента в формулах для средней длины свободного пробега, а температурная зависимость должна иметь одинаковый характер. В частности, выражение для 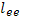(средняя длина свободного пробега при электрон-электронных столкновениях) должно совпадать с выражением для 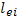с точностью до численного коэффициента, не очень сильно отличающегося от единицы. 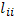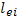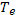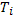Формула для (средняя длина свободного пробега при ион-ионных столкновениях) получается из формулы для при замене на Значения 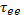и 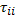близки друг к другу. Отношение 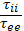равно 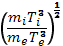. При равных электронной и ионной температурах ион-ионные соударения происходят гораздо реже, чем электрон -электронные или электрон-ионные. Рассеивающими свойствами обладают не только хаотические микрополя отдельных заряженных частиц, но и электрическое поле плазменных колебаний. Попытаемся хотя бы грубо оценить длину свободного пробега электрона из-за взаимодействия с равновесными (Рэлея—Джинса) колебаниями плазмы. Воспользуемся для этого формулой 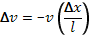. Пусть Δx порядка нескольких дебаевских длин, т. е. порядка самых коротких длин плазменных колебаний. Изменение продольной скорости на этом расстоянии составит 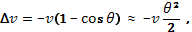где θ — угол отклонения электрона под действием поперечной компоненты электрического поля колебаний 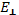. Значение этого угла можно считать равным отношению средней поперечной скорости, приобретаемой электроном в поле 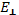., к продольной скорости 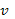. Следовательно, угол 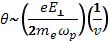. Отсюда

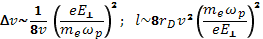
Принимая во внимание, что 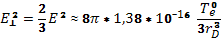получаем 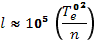. Таким образом, при грубой оценке вклад поля колебаний с 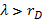в процессы рассеяния электронов оказывается примерно на порядок (в кулоновский логарифм раз) меньше вклада, который дают элементарные акты кулоновского столкновения частиц. Строгий расчет показывает, что и элементарные акты кулоновского рассеяния и рассеяние на колебаниях плазмы могут быть выведены как частные случаи взаимодействия частиц с флюктуациями микрополя. При этом «парные» столкновения— это результат рассеяния на флуктуациях микрополя, пространственные размеры которого меньше 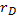. Флуктуации же с 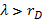надо рассматривать как суперпозицию плазменных колебаний. Таким образом, длина пробега электрона за рассеяния на термодинамически равновесном фоне плазменных колебаний на порядок величины больше пробега по отношению к парным соударениям. Но плазма часто оказывается неустойчивой: амплитуды плазменных колебаний самопроизвольно -нарастают до значений, которые во много раз превышают равновесные. В таких случаях длина свободного пробега определяется рассеянием на колебаниях. Такие плазмы обладают аномальными свойствами. С введением понятия «длина свободного пробега» удобно еще раз вернуться к разделению плазм на идеальные и неидеальные. Условия идеальности можно переписать так: 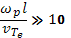. Это условие означает, что за время одного периода колебания столкновений практически не происходит. В случае неидеальной плазмы столкновения становятся столь частыми, что колебания затухают слишком быстро и само понятие колебаний теряет смысл.

Подведем некоторые итоги. С помощью проведенного выше анализа мы попытались включить взаимодействие заряженных частиц в плазме в рамки элементарной кинетической теории газов, заменяя плавно изгибающиеся траектории электронов и ионов условными ломаными линиями и сводя статистический эффект многих слабых столкновений к одному условному сильному удару. Польза от применения таких не очень корректных методов заключается в том, что имея формулы для средней длины свободного пробега, среднего времени между ударами и т. д., можно оперировать наглядными картинами при анализе основных физических процессов в плазме. Существует, однако, вполне корректный метод анализа кулоновского взаимодействия частиц в плазме, основанный и а использовании математического аппарата теории кинетических уравнений.

Остановимся теперь на вопросе об обмене тепловой энергией между электронами и ионами в плазме. Рассмотрим сначала самый простой случай. Пусть быстрый электрон с импульсом 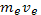пролетает мимо неподвижного иона и испытывает рассеяние на угол θ . при этом иоиу передается импульс (рис. 1.4). 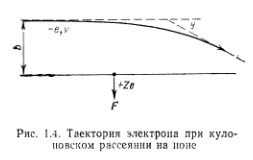Под действием этого импульса ион приходит в движение, приобретая кинетическую энергию

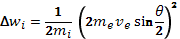
Чтобы найти энергию, которую быстрый электрон передает подвижным ионам за единицу времени, нужно умножить 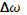на 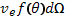и проинтегрировать по углам:

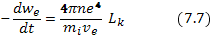
(предполагается, что ионы имеют единичный заряд). Выражение для передаваемой энергии преобразуем следующим образом:

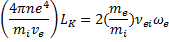
Здесь 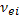— число столкновений между электроном с кинетической энергией 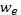и неподвижными ионами в единицу времени. Относительная доля энергии, теряемая в среднем при одном столкновении, составляет (как и следовало ожидать для наглядной модели упругого удара двух шаров). Среднее значение энергии 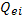которую электрон плазмы передает ионам за 1 с, получается из (7.7) интегрированием по максвелловскому распределению по скоростям:

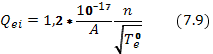
Здесь А — атомная масса ионизованного газа. Указанная формула справедлива только при 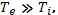если одного порядка, то выражение (7.9) должно быть заменено на следующее:

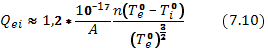
Для того чтобы получить представление о степени эффективности теплообмена между электронами и ионами плазмы, обратимся к конкретному примеру. Пусть температура электронов в водородной плазме поддерживается на уровне 10⁶ К при концентрации n=10¹³ см^-3. Чтобы нагреть ионы от нулевой температуры до 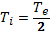, при этих условиях потребуется 1,2 мс. Заметим, что результат такого вычисления имеет смысл только в том случае, если в течение рассматриваемого промежутка времени ионы сохраняют всю приобретаемую ими энергию. Ион с энергией, соответствующей температуре в несколько сот тысяч градусов, за 1 мс проходит примерно 100 м. Для того чтобы в этих условиях ионная компонента могла нагреваться, необходима эффективная термоизоляция плазмы. Если тепловая скорость электронов значительно превышает тепловую скорость ионов, то формула (1.17) остается справедливой и при 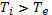, т. е. в том случае, когда происходит нагрев электронов более горячей ионной компонентой. Перепишем для этого случая указанную формулу в виде

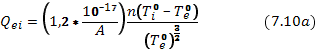
где 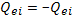— энергия, передаваемая от ионов к электронам в единице объема за 1 с. Однако если в плазме "с холодными электронами присутствуют настолько горячие ионы 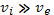, то скорость теплообмена может значительно возрасти. Рассуждая так же, как и при выводе формулы (7.7), при указанном условии приходим к следующей формуле для теплопередачи:

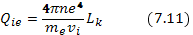
или после интегрирования по максвелловскому распределению ионов

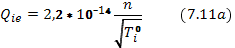
Одной из основных характеристик вещества служит уравнение состояния, т. е. соотношение между давлением, плотностью и температурой. Для классической плазмы с изотропным распределением по скоростям заряженных частиц уравнение состояния имеет тот же вид, что и для идеального газа с двумя компонентами: 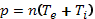. Здесь р — давление плазмы, равное сумме электронного и ионного давлений. Как уже указывалось выше, эта формула справедлива для случаев, когда 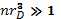. Обычно предполагается, что распределение частиц газа по энергиям подчиняется закону Максвелла. По отношению к плазме это предположение нельзя считать бесспорным. Максвелловский энергетический спектр устанавливается в результате столкновений между частицами газа. Для того чтобы в данном коллективе частиц при произвольном начальном энергетическом распределении установилось распределение по Максвеллу для широкой области энергий, т. е., чтобы успел «отрасти» максвелловский «хвост», содержащий частицы с энергией 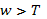, должно пройти время, за которое частицы должны испытать в среднем донесколько столкновений друг с другом. Причем речь идет о столкновениях идентичных частиц. В частности, максвелловское распределение по энергиям у электронов практически установится за промежуток времени, примерно в десять раз превышающий среднее время 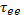между двумя электронными столкновениями. В ионной компоненте максвелловское распределение устанавливается после десятка ионных соударений. Следовательно, при 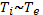«максвеллизация» у ионов происходит гораздо медленнее, чем у электронов (в отношении 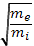). Необходимо отметить, что в каждой из компонент плазмы процесс максвеллизации, который едет из-за столкновений между идентичными частицами, протекает быстрее, чем установление теплового равновесия между обеими компонентами. Поэтому в плазме электроны и ионы могут быть распределены по Максвеллу, но при двух различных значениях температуры. Кроме того, если время жизни заряженных частиц плазмы мало, то у ионной компоненты в области энергий, во много раз превышающих температуру ионов, энергетическое распределение может резко отличаться от максвелловского (число таких быстрых ионов во много раз меньше, чем это следует по закону Максвелла, если нет каких-либо механизмов ускорения).

(источник:Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков, гл.1, §1.4)

Термодинамика плазмы. Понятие о локальном термодинамическом равновесии (ЛТР) плазмы. Температура компонент плазмы. Кулоновская поправка к внутренней энергии плазмы. Основные ионизационные и рекомбинационные процессы в плазме. Ионизационное равновесие. Формула Саха для термодинамически равновесной плазмы и ее вывод из квазиклассической статистики. Степень ионизации термоядерной плазмы.