Электрический дрейф

Оба вида дрейфа в неодно­родном магнитном поле зависят от знака частиц. От них отличается в этом отношении электрический дрейф, т. е. дрейф ча­стиц в магнитном поле при на­личии электрического. Скорость электрического дрейфа

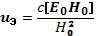(6.47)

Действительно, электрический заряд в формулу не входит, а с ним исключается зависимость скорости от знака частиц. Электрический дрейф для ионов и для электронов происходит в одну сторону и с одинаковой скоростью, несмотря на большое различие в их массах.

Следует иметь в виду, что формула (6.47) примени­ма только при Е₀<<Н₀, иначе скорость дрейфа получается соизмеримой со скоростью света. Весь же наш вы­вод для дрейфовых скоростей сделан исходя из по­стоянства массы частиц, т. е. для нерелятивистских ско­ростей.

Формулу (6.47) мы получили, подставив в общее вы­ражение (6.43) для скорости дрейфов в магнитном поле значение электрической силы

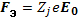(6.48)

Однако ее можно вывести несколько иначе — из об­щего уравнения (6.1). Это целесообразно, если учитывать некоторые полученные полезные физические вы­воды.

Преобразуем уравнение (6.1) в систему отсчета, ко­торая движется относительно исходной (лабораторной) системы координат с постоянной скоростью u'_Д. Ско­рость частицы в движущейся системе u', имлульср'. Скорость в лабораторной системе координат

(6.49)

Импульс

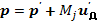(6.50)

Найдем изменение импульса р:

(6.51)

где Е_0||и Е_0⊥,—слагающие электрического поля вдоль и перпендикулярно магнитному полю.

Величинуu'_Д можно выбрать таким образом, чтобы выполнялись два условия:

(6.52)

и

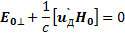(6.53)

Условия (6.52) и (6.53) определяют u'_Дсовершенно однозначно. Из условия (6.52) сразу же следует, чтоu'_Д⊥Н₀. Умножим второе условие (6.53) векторно наН_о:

(6.54)

Член H₀/c·(u'_ДН₀₎=0 согласно условию (6.52). Следовательно,

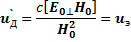(6.55)

т.е. представляет собой дрейфовую скорость. Уравнение движения (6.51) при учете (6.53) запишем

(6.56)

Из него полностью выпала компонента E_0пер. Отсюда можно сделать вывод, что влияние E_0пер сводится к созданию дрейфа в направлении, перпендикулярном к магнитному полю. Таким образом, получаем равномерно ускоренное движение вдоль поля и дрейфовое поперек него. Оба движения складываются в движение по па­раболе (рис. 8 ). Если Е₀ лежит в плоскости уz, то и ведущий центр не выйдет из этой плоскости. Поскольку выбор осей х и у произволен, случай, показанный на рис. 8, можно считать довольно общим.