Прямое и обратное преобразование Гильберта.

По ряду причин, часть из которых станет понятной из дальнейшего, в качестве сопряжённого удобно выбрать преобразованный по Гильберту исходный сигнал:

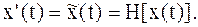
(1.4)

Комплексный сигнал вида 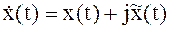называют аналитическим сигналом.

Преобразование Гильберта H[x(t)] в спектральной области сводиться к сдвигу фаз всех спектральных составляющих сигнала x(t) на угол 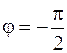в области положительных (ω>0) и на в 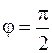области отрицательных (ω<0) частот.

С точки зрения схемотехники преобразователь Гильберта – это фазовращатель (рисунок 1) с передаточной функцией, которая представлена следующим выражением:

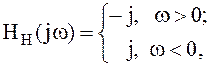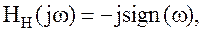
	(1.5)
где		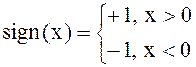–	знаковая функция.

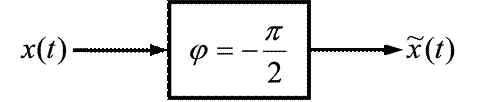
Рисунок 1.3 – Преобразователь Гильберта

Найдём импульсную характеристику преобразователя Гильберта

Первый интеграл в полученном выражении равен 0 в силу интегрирования нечётной функции при симметричных пределах, а второй сводиться к табличному интегралу вида:

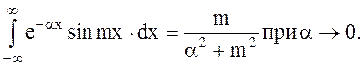
(1.6)

Окончательно получаем:

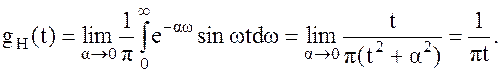
(1.7)

Из полученного результата с очевидностью вытекает невозможность физической реализации преобразования Гильберта, так как 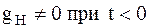. Тем не менее, реально преобразования Гильберта осуществляют приближённо, допуская временную задержку, тем большую, чем выше требования к точности преобразования.

Рассмотрим преобразование Гильберта во временной области. Из рисунка 1.3 вытекает:

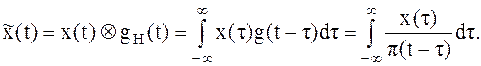
	(1.8)
где		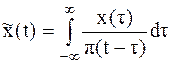–	прямое преобразование Гильберта.

Поскольку

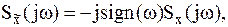
(1.9)

после умножения обеих частей равенства на jsign(w) получим

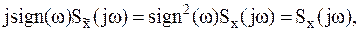
(1.10)

откуда следует, что передаточная функция обратного преобразования Гильберта H^-1[x(t)]отличается от передаточной функции прямого только знаком:

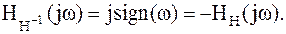
(1.11)

Соответственно:

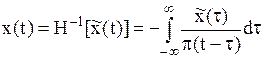– обратное преобразование Гильберта.