Представление действительного сигнала x(t) через его квадратурные компоненты
Любой действительный сигнал x(t) можно записать в виде:
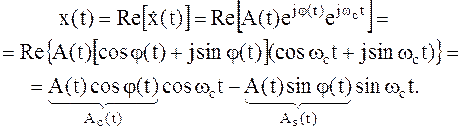
| (1.20) | |||
| где | Ac(t) = A(t)×cosj(t) | – | косинусная квадратурная компонента сигнала; | |
| As(t) = A(t)×sinj(t) | – | синусная квадратурная компонента сигнала; | ||
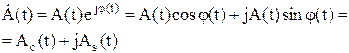 – комплексная огибающая. – комплексная огибающая.
| ||||
Представление x(t) через квадратурные компоненты особенно полезно для узкополосных сигналов, у которых они оказываются медленно меняющимися функциями по сравнению с coswct (при выборе wc внутри спектра сигнала x(t)). Формально условие узкополосности сигнала «в расширенном смысле» можно записать следующим образом
Fв < fс, где Fв – верхняя частота в спектре Ас(t) и Аs(t).
Обработку узкополосных сигналов можно выполнить проще и точнее через обработку их квадратурных компонентов. Действительно, если выполняется условие узкополосности сигнала, то спектр комплексного сигнала вида:
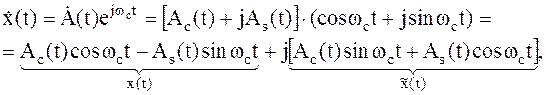
| (1.21) |
получаемого сдвигом спектра огибающей 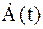 вверх на wc, полностью располагается в области положительных частот, следовательно, этот сигнал – аналитический и его мнимая часть является преобразованием Гильберта действительной части:
вверх на wc, полностью располагается в области положительных частот, следовательно, этот сигнал – аналитический и его мнимая часть является преобразованием Гильберта действительной части:
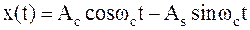
| (1.22) |
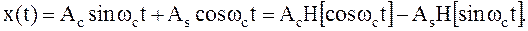
|
Таким образом, можно считать, что преобразование Гильберта узкополосного сигнала сводиться к сдвигу фаз на угол - 90° гармонических колебаний coswctи sinwct и его квадратурных компонентов.
На рисунке 1.2. приведена векторная диаграмма аналитического сигнала. Она представляет собой комплексную плоскость с вращающимися и меняющим свою длину вектором 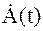 . Угловая скорость его вращения изменяется во времени по закону:
. Угловая скорость его вращения изменяется во времени по закону:
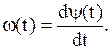
| (1.23) |
.
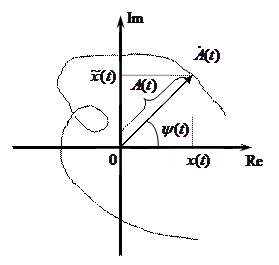
Рис. 2. Векторная диаграмма
Выводы:
1 Узкополосные сигналы удобно представлять в виде аналитического сигнала.
2 Приём узкополосных сигналов осуществляется с помощь операции разложения его на квадратурные компоненты
Заключение
Сложные преобразования показывают, что центрированная корреляционная функция огибающей приближенно равна квадрату огибающей корреляционной функции исходного узкополосного сигнала. Спектральная плотность мощности огибающей имеет два слагаемых: дельта-функцию, соответствующую постоянной составляющей огибающей, и спектральную плотность флюктуационной составляющей, которая является преобразованием Фурье от квадрата огибающей корреляционной функции исходного узкополосного сигнала.
Литература
Основная:
1. Теория электрической связи: Учеб. Для вузов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и связь, 1998. – 433 с.
Дополнительная:
1. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.
2. Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
3. Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
4. Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
Разработал:
| кандидат технических наук |
| О.Р. Кивчун |
| «___»__________ 2012 года |
Дата добавления: 2017-11-21; просмотров: 1685;











