ИЗОХОРНО-ИЗОТЕРМИЧЕСКИЙ И ИЗОБАРНО-ИЗОТЕРМИЧЕСКИЙ ПОТЕНЦИАЛЫ

В химической термодинамике считается, что убыль внутренней энергии положительна, а теплота, сообщенная системе, отрицательна. Уравнения первого и второго законов термодинамики с учетом принятых знаков будут иметь вид

;

.

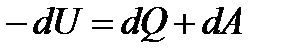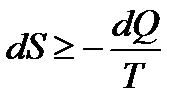Объединяя эти уравнения, получим

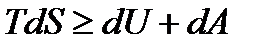. (13.16)

Если учитывать только работу изменения объема, то 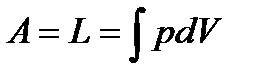. Тогда

соотношение (13.16) примет вид

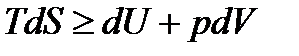. (13.17)

Или в записи через энтальпию

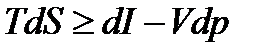. (13.18)

Преобразуем уравнение (13.17) следующим образом

;

;

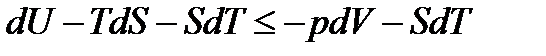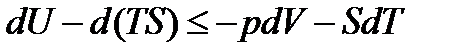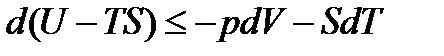, (13.19)

где 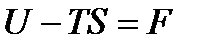является некоторой функцией состояния, которая была назва­на выше (см. §5.1) изохорно-изотермическим потенциалом.

Соотношение (13.19) перепишем в виде

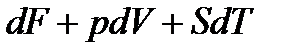. (13.20)

В изохорно-изотермических процессах V = const, T = const. Следователь­но, 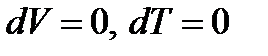. Тогда (13.20) примет вид

.

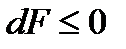Отсюда следует, что в изолированных системах, находящихся при посто­янной температуре и объеме, самопроизвольно могут протекать только те процессы, которые сопровождаются уменьшением изохорно-изотермического потенциала F. Причем минимум F = F_min наблюдается в со­стоянии равновесия. При этом

.

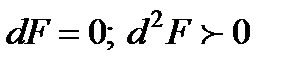Если рассматривать функцию F как функцию независимых параметров Т и V, то ее полный дифференциал будет

.

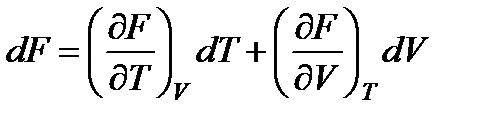Сопоставляя это соотношение с соотношением (13.20), получим

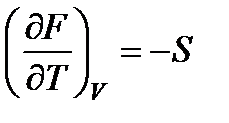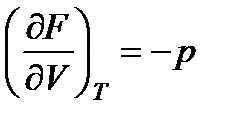; . (13.21)

Из этих равенств следует, что изменение F по температуре при постоян­ном объеме определяется величиной энтропии, а изменение F по объему при постоянной температуре - величиной давления. Таким образом, F является характеристической функцией, так как ее частные производные позволяют определить термодинамические свойства системы (см. § 5.1).

Подставляя величину энтропии из (13.21) в формулу 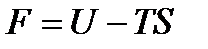, получим

аналитическое выражение уравнения, связывающего изохорно-изотермический потенциал с внутренней энергией

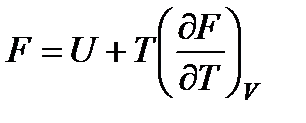. (13.22)

Если к обеим частям уравнения (13.17) прибавить соотношение 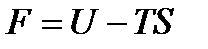, то после некоторых преобразований получим

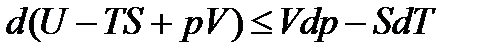. (13.23)

Обозначим

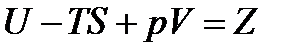. (13.24)

Отсюда Z = F+pV или 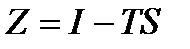, так как I = U+pV.

Величина Z из уравнения (13.24) выше (см. § 5.1) была названа изобарно-изотермическим потенциалом и является некоторой функцией состояния. Из (13.23) следует

.

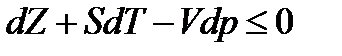Так как в изобарно-изотермических процессах dT=0, dp=0, то

.

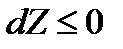Отсюда следует, что в изобарно-изотермических процессах в изолирован­ной системе самопроизвольно могут протекать только такие процессы, кото­рые сопровождаются уменьшением Z и в пределе (в состоянии равновесия) достигается некоторое минимальное значение этой величины, т.е.

.

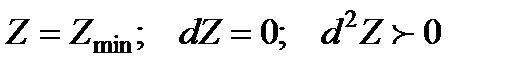Как следует из (13.24), функция Z является характеристической функцией при независимых параметрах р и T. Ее полный дифференциал будет

.

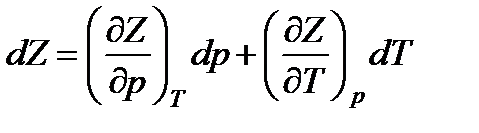Сравнивая это уравнение с равенством (13.24), получим

.

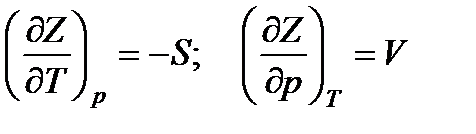Подставляя найденное значение энтропии в формулу , получим уравнение, связывающее изобарно-изотермический потенциал с энтальпией

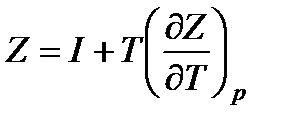. (13.25)

Таким образом, в некоторых частных случаях в качестве критерия равно­весия системы можно использовать изохорно- и изобарно-изотермический потенциалы. Условием равновесия процессов при (V,t)= const и (p,T)= const является минимум этих потенциалов. Функции F и Z характери­зуют ту часть внутренней энергии или энтальпии, которая может переходить в полезную работу.