Запаздывающие потенциалы.

В предыдущем разделе было показано, что векторный и скалярный потенциалы нестационарного электромагнитного поля удовлетворяют неоднородным уравнениям Даламбера и условиям калибровки Лоренца

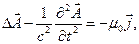
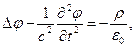
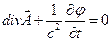. (1)

Для стационарных условий соотношения (1) переходят в уравнения Пуассона для потенциалов 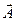и 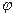и условие калибровки векторного потенциала:

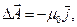
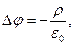
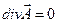. (2)

Для векторного и скалярного потенциалов справедливы следующие зависимости

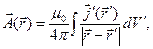
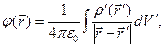(3)

их называют ньютоновыми или объёмными потенциалами или интегралами Пуассона. Можно показать, что в условиях магнитостатики условие калибровки (2) для магнитного потенциала в форме (3) действительно выполняется. В выражениях (3) штрихом помечены переменные, связанные с источниками электромагнитного поля, величины без штрихов описывают положение точки наблюдения.

Поскольку точка наблюдения 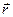в общем случае не совпадает с точкой расположения источника поля 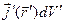или 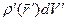, то в силу принципа близкодействия (сигнал из точки пространства 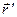в точку пространства 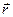распространяется в вакууме со скоростью с) между событиями «изменение состояния источника поля» и «изменение состояния поля в точке наблюдения» должно пройти «время запаздывания»:

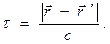(4)

Можно предположить, что в нестационарном случае соотношения (3) преобразуются к виду:

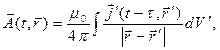
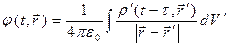. (5)

В расширенных курсах теоретической физики показано, что выражения (5) действительно являются строгими решениями уравнений (2).

Итак, физический смысл запаздывающих потенциалов (5) электромагнитного поля заключается в том, что электромагнитное поле в точке наблюдения в рассматриваемый момент времени полностью определяется распределением в пространстве источников электромагнитного поля в предыдущие моменты времени, причём время запаздывания 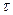для каждого элементарного источника поля определяется соотношением (4).

Напомним, что напряжённость электрического поля и индукция магнитного поля связаны с потенциалами переменного электромагнитного поля соотношениями:

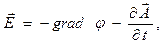
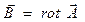. (6)

Соотношения (6) позволяют вычислить векторы напряжённости электрического поля и индукции магнитного поля как функции от объёмной плотности источников электромагнитного поля 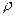и 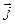, дифференцирование в правых частях соотношений (5) осуществляется по координатам точки наблюдения (не штрихованные переменные). Предполагаем при этом, что дифференцировать интегралы «по параметру» можно, дифференцируя по параметру подынтегральные функции. Вычисление необходимо проводить с учётом определения времени запаздывания (4).

Опустим громоздкие выкладки и рассмотрим окончательные результаты:

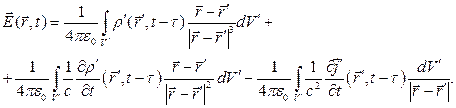(7)

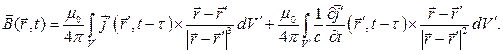(8)

При анализе зависимостей (7) и (8) следует обратить внимание на то, что переменное векторное поле напряжённости 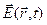зависит не только от «распределения» по пространству объёмной плотности электрического заряда, но и от скорости её изменения во времени, а также и от скорости изменения во времени объёмной плотности тока проводимости. Векторное поле магнитной индукции 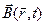зависит не только от «распределения» по пространству объёмной плотности тока проводимости, но и от скорости изменения её от времени. Важно заметить, что различен характер убывания с расстоянием между точкой наблюдения и элементарным источником поля подынтегральных выражений в каждом из интегралов (7) или (8). А если ещё заметить, что время запаздывания 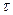не одно и то же для разных значений радиус-вектора 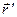, то раскрывается смысл термина «распределение» по пространству и становится понятным, насколько переменное электромагнитное поле «сложнее» стационарных электрического и магнитного полей.

В заключение обратим внимание читателя на то, что векторный и скалярный потенциалы электромагнитного поля (5) связаны между собой условием лоренцевой калибровки (1). Другими словами говоря, объёмную плотность тока проводимости нельзя рассматривать независимо от объёмной плотности электрического заряда. В этом случае необходимо иметь в виду, что вектор магнитной индукции неявно, но зависит от объёмной плотности электрического заряда. Это взаимопроникновение друг в друга источников электромагнитного поля должно приводить к взаимной зависимости друг от друга переменных во времени электрического и магнитного полей. Отмеченное свойство электромагнитного поля непосредственно и очень наглядно проявляется при анализе исходной системы уравнений Максвелла.