Следствия из преобразований Лоренца
Из преобразований Лоренца следуют важные выводы: оказалось, что размеры движущихся тел, их массы, течение времени
зависят от скорости движения. Рассмотрим эти выводы подробно;
а) относительность одновременности событий. Замедление времени.
Пусть в инерциальной системе отсчета 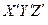 , движущейся относительно Земли со скоростью V, близкой к с (например, в воображаемом космическом корабле) в одном и том же месте произошли два события (космонавт встал и вновь сел в кресло). Интервал времени между этими событиями в штрихованной системе отсчета
, движущейся относительно Земли со скоростью V, близкой к с (например, в воображаемом космическом корабле) в одном и том же месте произошли два события (космонавт встал и вновь сел в кресло). Интервал времени между этими событиями в штрихованной системе отсчета 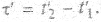 . Для наблюдателя в системе координат X Y Z, связанной с Землей, соответствующий интервал времени определится как
. Для наблюдателя в системе координат X Y Z, связанной с Землей, соответствующий интервал времени определится как
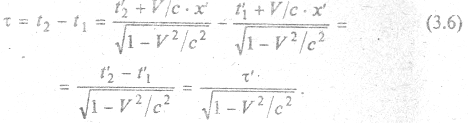
Каким образом, интервал времени между одними и теми же событиями для наблюдателей, находящихся в разных системах отсчёта, различен 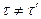 . Следовательно, время не абсолютно, и темп его течения зависит от системы отсчета, а именно: движущиеся относительно наблюдателя часы кажутся ему идущими медленнее, чем часы находящиеся в системе отсчета наблюдателя;
. Следовательно, время не абсолютно, и темп его течения зависит от системы отсчета, а именно: движущиеся относительно наблюдателя часы кажутся ему идущими медленнее, чем часы находящиеся в системе отсчета наблюдателя;
б) относительность расстояний. Сокращение длин тел.
Пусть в инерциальной системе XYZ покоится линейка, расположенная параллельно оси X. Ее длина в этой системе отсчета 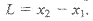 . В системе отсчета
. В системе отсчета 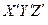 движущейся со скоростью V вдоль оси X дайна линейки
движущейся со скоростью V вдоль оси X дайна линейки 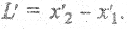
На основании (3.5) получим

Таким образом, с точки зрения наблюдателя находящегося в неподвижной системе отсчета, размеры движущихся тел в направлении относительного движения уменьшаются при стремлении V → c.
Прекрасным примером замедления времени по уравнению (3.6) и сокращения длины по уравнению (3.7) является распад мю-мезонов, нестабильных частиц, создаваемы в атмосфере космическими частицами. Время жизни - от рождения до распада — мю-мезона в среднем равно 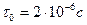 . Типичная скорость v мезонов около 2,994 ∙ 108 м/с, т. е. 0,998 от скорости света в вакууме (с). Очевидно, что за время жизни частица может пройти расстояние
. Типичная скорость v мезонов около 2,994 ∙ 108 м/с, т. е. 0,998 от скорости света в вакууме (с). Очевидно, что за время жизни частица может пройти расстояние 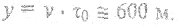 В действительности частицы рождаются на высотах порядка 10 км. Этот кажущийся парадокс объясняется специальной теорией относительности. Рассмотрим систему отсчета, связанную с мезоном.
В действительности частицы рождаются на высотах порядка 10 км. Этот кажущийся парадокс объясняется специальной теорией относительности. Рассмотрим систему отсчета, связанную с мезоном.
Время жизни мезона в ней равно 2 ∙ 10-6 с, так как не подвержено воздействию движения. Расстояние же от мезона до Земли «представляется» мезону сокращенным:

В системе отсчета, связанной с Землей, расстояние равно у0, время жизни мезона для земного наблюдателя представляется возросшим до величины ~31,7 ∙ 10-6 с, (почти в 16 раз);
в) релятивистское правило сложения скоростей.
Если тело равномерно движется со скоростью vx вдоль оси X в системе X Y Z, то его скорость 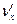 в системе
в системе 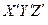 движущейся со скоростью V относительно первой, равна
движущейся со скоростью V относительно первой, равна

Очевидно, при V << с имеем классический случай 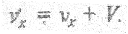
При vx = с (или при V = с, или при vx = V= с) результирующая скорость равна предельному' значению, т. е. 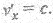
Дата добавления: 2017-11-21; просмотров: 1176;











