Преобразования Лоренца как следствие постулатов Эйнштейна

Напомним, что формулы преобразований Лоренца, т. е. пере­хода от одной инерциальной системы отсчета в другую, были по­лучены с использованием произвольных допущений о сокраще­нии длин тел. В специальной теории относительности преобразо­вания Лоренца получаются как прямое следствие постулатов Эйнштейна.

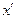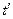Пусть штрихованная инерциальная система отсчета движется относительно нештрихованной со скоростью V вдоль оси X. Найдем и если известны х и t. При этом полагаем, что в обеих системах отсчета - неподвижной и движущейся - свет распространяется с одинаковой скоростью с (второй постулат Эйнштейна). Для светового луча, распространяющегося вдоль оси Х (и 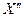) в положительном направлении справедливо

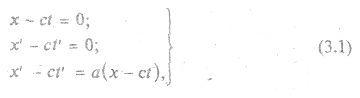
где а - некоторая постоянная.

Аналогично, для луча, распространяющегося в отрицательном направлении

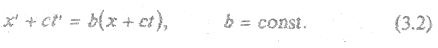
Решая (3.1) и (3.2) совместно, получим:

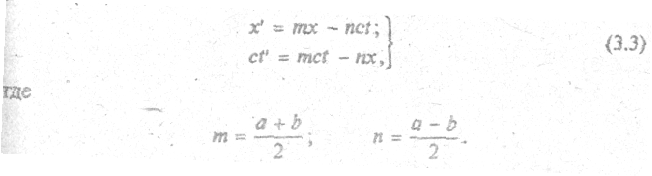
Для начала координат движущейся системы ( 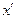= 0) из первого уравнения (3.3)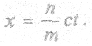

Следовательно, 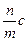есть скорость, с которой штрихованная система движется относительно нештрихованной (и наоборот): 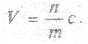Для определения отношения n/m воспользуемся первым постулатом Эйнштейна - принципом от­носительности. Определим из нештрихованной системы отсчета длину L некоторого тела, покоящегося в штрихованной системе отсчета. Для момента t = 0 из первого уравнения (3.3) следует 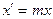. Пусть длина тела L в системе, где оно покоится (т.е. в штрихованной) равна длине отрезка оси от 0 до точки 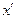(L = 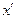). Тогда с точки зрения наблюдателя, находящегося в не­штрихованной системе отсчета, длина тела будет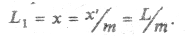

Теперь из штрихованной системы отсчета

в момент 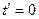определим длину тела в нештрихованной системе.

Из второго уравнения (3.3) следует, что

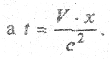
Подставив значение t в первое уравнение (3.3), получим:

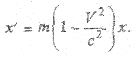
С точки зрения наблюдателя, находящегося в нештрихованной системе отсчета, длина тела равна

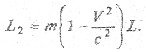
На оснований принципа относительности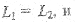

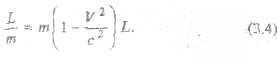
Уравнение (3.4) можно переписать в виде

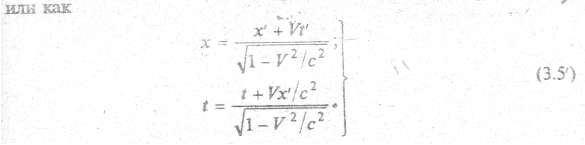
Это и есть преобразование времени и координат при переходе

из одной инерциальной системы в другую — преобразования Лоренца. Из уравнений (3.5) и (3.5’) следует:

- результаты измерения как времени, так и координат зависят

от системы отсчета наблюдателя;

- при V << с эти выражения (3.5) переходят в (1.5), т. е. преобразования Галилея являются предельным случаем, а законы классической механики Ньютона справедливы при скоростях движения, значительно меньших с;

- при V >> с преобразования (3.5) становятся мнимыми, т. е. движение со сверхсветовыми скоростями и формально математи­чески запрещено. Механика, учитывающая наличие предельной скорости, называется релятивистской. Таким образом, конкрет­ный характер связи пространства-времени и движения вытекает из наличия предельной скорости передачи взаимодействий - скорости света в вакууме.