Уравнений классической электродинамики (уравнения Максвелла)

Всякое решение уравнений поля должно описывать поле, ко­торое может существовать в Природе, Согласно принципу супер­позиции, сумма любых таких полей также должна представлять реально возможное поле. Линейные дифференциальные уравне­ния обладают таким свойством, что сумма любых решений урав­нения также является его решением. Следовательно, уравнения электромагнитного поля должны быть линейными дифферен­циальными уравнениями.

Система уравнений, описывающих электромагнитное поле, называется уравнениями Максвелла. Они являются основными уравнениями классической электродинамики Уравнения Макс­велла связывают в любой точке пространства и в любой момент времени силовые характеристики, определяющие электромагнит­ное поле ( 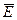, 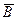) с характеристиками источников поля - вектором плотности электрического тока 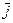и объемной плотностью элект­рического заряда ρ. Уравнения Максвелла в интегральной форме оперируют понятиями потока и циркуляции вектора (М 5.3).

Первое уравнение определяет, что электрическое поле порожда­ется электрическими зарядами; это уравнение устанавливает связь между объемной плотностью заря­да ρ и вектором .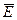

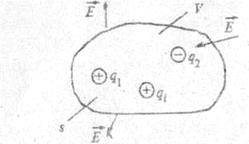Рис. 2.2.

Пусть в пространстве выделена некоторая область объемом V, ограниченная замкнутой поверх­ностью S, а в этом объеме произвольным образом распределен заряд q, так, что объемная плотность заряда ρ (рис. 2.2). Это оз­начает, что 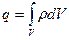. Первое уравнение, носящее название теоремы Гаусса, определяет, что поток вектора напряженности 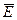электрического поля, создаваемого в вакууме зарядом q, через поверхность S пропорционален заряду, находящемуся в объеме V:

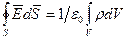. (2.5)

Здесь ε₀- постоянный коэффициент, называемый электрической постоянной.

Силовые линии электрического поля, созданного зарядами, разомкнуты, они начинаются и оканчиваются на зарядах или уходят в бесконечность.

Второе уравнение определяет еще один источник электричес­кого поля - изменяющееся во времени магнитное поле. Это уравнение является обобщением закона электромагнитной индук­ции Фарадея.

Пусть в пространстве выделен некоторый замкнутый контур L, ограничивающий поверхность S. Пусть существует магнитное поле индукцией 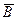, поток которого через поверхность S равен 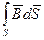и изменяется во времени. Второе уравнение определяет, что при этом возникает электрическое поле, циркуляция вектора напряженности 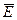которого по контуру L пропорциональна ско­рости изменения магнитного потока через поверхность S:

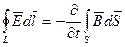. (2.6)

Чем быстрее изменяется магнитное поле, тем сильнее возни­кающее при этом (индуцированное) электрическое поле. Индуци­рованное поле носит вихревой характер. Знак “минус” перед пра­вой частью уравнения (2.6) отвечает правилу Ленца.

Третье уравнение определяет факт отсутствия в Природе маг­нитных зарядов (подобных электрическим) как источников маг­нитного поля; поток вектора магнитной индукции через произ­вольную замкнутую поверхность S равен нулю:

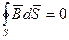. (2.7)

Магнитное поле всегда носит вихревой характер; магнитные силовые линии всегда замкнуты.

Четвертое уравнение определяет, что источником магнитного поля являются движущиеся электрические заряды (т. е. электри­ческий ток) и изменяющееся во времени электрическое поле:

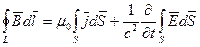. (2.8)

Циркуляция вектора 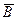по произвольному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна сумме двух слагаемых: первое из них пропорционально плотности 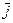электрического тока, протекающего сквозь контур, второе — про­порционально скорости изменения потока электрического поля через поверхность S, ограниченную контуром L.

Из (2.6) и (2.8) следует, что электрическое и магнитное поля нельзя в общем случае рассматривать независимо. Они составля­ют неразрывную совокупность — электромагнитное поле. К этому вопросу мы вернемся при изучении теории относительности

(гл. 3).

Рассмотренные уравнения (2.5) - (2.8) называются интегральны­ми. Их можно записать с использованием дифференциальных характеристик (МП 5.2) в виде системы дифференциальных уравнений:

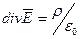; (2.5')

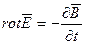; (2.6')

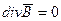; (2.7')

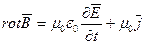. (2.8')

Переход к дифференциальной форме осуществляется с по­мощью теорем Гаусса и Стокса (МП 5.4). Покажем для примера связь между уравнениями (2.5) и (2.5'). На основании теоремы Гаусса левая часть уравнения (2.5) преобразуется к интегралу по объему 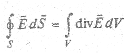Заменяя левую часть уравнения (2.5) этим интегралом, получим:

С использованием дифференциальных характеристик удобно сформулировать закон сохранения электрического заряда. Так как заряд электрически изолированной системы сохраняется, то уменьшение заряда в некотором объеме в единицу времени равно силе тока через поверхность, ограничивающую этот объем, т. е.

тогда

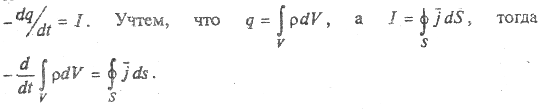
Применим к правой части интегральную теорему Гаусса:

где интегрирование ведется по одному и тому же объему, следо­вательно,

Полученное уравнение называется уравнением непрерывности.

Четыре рассмотренных уравнения поля в интегральной и диф­ференциальной формах представляют собой единую систему уравнений Максвелла для электромагнитного поля в вакууме. Она полностью определяет электромагнитное поле, если известны расположение и движение электрических зарядов. Уравнение Максвелла вместе с выражением для силы Лоренца (2.3) пред­ставляют наиболее общие законы электромагнетизма. Все осталь­ное содержание электродинамики составляют выводы и след­ствия, полученные с помощью математических преобразований уравнений Максвелла-Лоренца для конкретных систем полей, зарядов и токов.

Например, из уравнений (2.5') и (2.8') следует закон сохране­ния электрического заряда в форме (2.9). Продифференцировав обе части уравнения (2.5') по времени, получим:

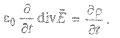
Обе части уравнения (2.8') умножим на 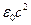и возьмем дивергенцию от каждой части:

Дивергенция от ротора любого вектора по определению равна нулю. В правой части (2.10) поменяем местами операции диффе­ренцирования и дивергенции:

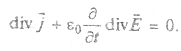
Заменяя второй член этого уравнения на 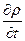окончательно получим

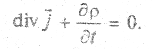
Прямо вытекает из второго уравнения Максвелла (2.6) закон электромагнитной индукции Фарадея. Интеграл в правой части уравнения по определению есть магнитный поток 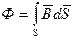, а циркуляция вектора 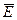по произвольному замкнутому контуру L (левая часть уравнения) называется электродвижущей силой (э.д.с.). Если заменить контур проводником, то получим, что э.д.с., наводимая при изменениях магнитного поля во времени, равна взятой со знаком “минус” скорости изменения магнитного потока через поверхность, натянутую на проводник:

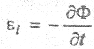
Стационарные электрические и магнитные доля существуют, если расположение зарядов неизменно во времени и электричес­кие токи постоянны. В этом случае 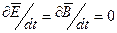, и система уравнений Максвелла распадается на две пары независимых урав­нений:

Первая пара уравнений описывает электростатическое поле (поле неподвижных зарядов), а вторая - магнитостатическое (по­ле постоянных токов). Из уравнений следует, что электростати­ческое поле потенциальное, а магнитостатическое - вихревое.

Важной характеристикой электростатического поля является потенциал, характеризующий потенциальную энергию заряда, находящегося в поле. Пусть заряд помещен в некоторую точку электростатического поля. Тогда потенциалом φ называется отно­шение потенциальной энергии U этого заряда к величине заряда:

На заряд действует со стороны поля сила, стремящаяся уменьшить его потенциальную энергию: 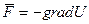. С другой стороны, 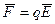. Приравнивая правые части выражений для 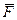, получим:

Формула (2.14) описывает связь напряженности и потенциала для электростатического поля.

Сила 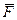, перемещая заряд q, совершает работу. При элемен­тарном перемещении 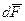работа равна.

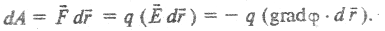
Работа сил поля на некотором участке траектории L опреде­ляется интегралом

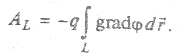
Из свойств интеграла (МП 3.2) следует, что интеграл от гpaдиента потенциала на некотором участке траектории 1-2 равен разности значений потенциала на концах участка, т. е.

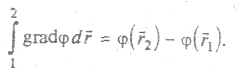
Здесь 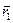, 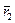радиус-векторы начала и конца участка траек­тории (рис. 2.3). Тогда работа А₁₂ равна произведению заряда на разность потенциалов

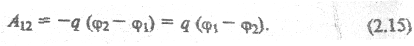
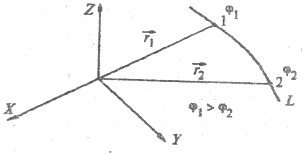Рис. 2.3.

Важно, что работа не зависит от вида траектории, а опреде­ляется только положением начала и конца последней. С выраже­нием (2.15) связана широко используемая в атомной физике и физике элементарных частиц внесистемная единица энергии - электровольт (эВ). 1 эВ — энергия, приобретаемая одним эле­ментарным зарядом (е) при прохождении им разности потен­циалов 1 В. Из (2.15) непосредственно следует, что работа сил потенциального поля при перемещении заряда по замкнутому контуру равна нулю, так как в этом случае .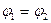

Вернемся к выражению элементарной работы 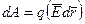. Так как работа по замкнутому контуру равна нулю 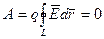, то равна нулю и циркуляция вектора 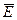по этому контуру (МП 5.3)

Выражение (2.16) дает необходимое и достаточное условие потенциальности поля. В противоположность электростатичес­кому магнитостатическое поле является вихревым и характери­зуется не скалярным, а векторным потенциалом.

Рассмотрим вывод из уравнений Максвелла некоторых законов электромагнетизма, полученных эмпирически.

Поле точечного заряда. Закон Кулона. Этот закон определяет силу взаимодействия двух неподвиж­ных точечных зарядов в вакууме.

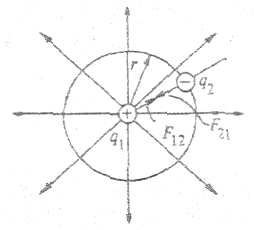Окружим точечный заряд q₁, нап­ример, положительный, сферой радиуса r (рис. 2.4).

Рис. 2.4.

Линии напряженности (силовые линии) поля, создаваемого этим зарядом, радиальны, поле обладает центральной симметрией. На поверхности сферы значение .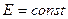

Воспользуемся ' первым уравнением Максвелла (2.5) —теоремой Гаусса

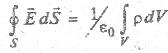
которое при выбранных условиях преобразуется к простому виду

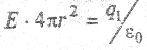
откуда

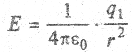
Направление вектора 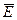в каждой точке сферы совпадает с нап­равлением соответствующего радиуса вектора 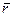, тогда

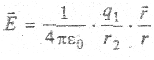
Полученная формула определяет напряженность электричес­кого поля точечного заряда в точках, удаленных от него на расстояние r. Поместим в любую точку на поверхности сферы другой точечный заряд q₂, например, отрицательный. По опре­делению напряженности, на него будет действовать сила притяжения — кулоновская сила.

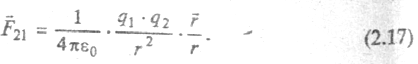
Если в наших рассуждениях заряды поменять местами, получим, что на заряд q₁ со стороны q₂, действует сила 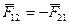. Следовательно, силовое взаимодействие зарядов подчиняется третьему закону Ньютона. Теорема Гаусса существенно облегчает расчет полей в случаях симметричных систем зарядов.

Магнитное ноле прямого тока. Из четвертого уравнения Максвелла (2.8) следует, что магнитное поле порождается, в част­ности, электрическим током. Получим выражение для магнитной индукции поля в простом Случае так называемого прямого тока — тока в бесконечно длинном линейном проводнике. Линии маг­нитной индукции в силу осевой симметрии задачи являются концен­трическими окружностями, располо­женными в плоскостях, перпендику­лярных проводнику. Одна из таких плоскостей изображена на рис. 2.5.

Рис. 2.5.

Направление силовых линий свя­зано с направлением тока правилом правою винта. Предположим, что переменное электрическое поле отсутствует, тоща уравнение (2.8) упростится:

Выберем одну из силовых линий радиуса r. Тогда в выражении (2.18)

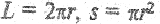и получим, что 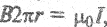откуда

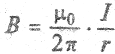
Эта формула определяет модуль вектора магнитной индукции магнитного поля, создаваемого током I в точках, отстоящих от проводника на расстояние r.