ДРОССЕЛЬНЫЙ ЭФФЕКТ (ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА)
Дроссельный эффект был обнаружен Джоулем и Томсоном опытным путем в 1852 г. [Опытами было установлено, что в результате дросселирования изменяется температура рабочего тела. Это явление было названо эффектом Джоуля-Томсона. Изменение температуры при дросселировании связано с тем, что в каждом реальном газе действуют силы притяжения и отталкивания между молекулами. При дросселировании происходит расширение газа, сопровождающееся увеличением расстояния между ними. Все это приводит к уменьшению внутренней энергии рабочего тела, связанному с затратой работы, что, в свою очередь, приводит к изменению температуры.
Температура идеального газа в результате дросселирования не изменяется, и эффект Джоуля-Томсона в данном случае равен нулю. Таким образом, изменение температуры реального газа при дросселировании определяется величиной отклонения свойств реального газа от идеального, что связано с действием межмолекулярных сил.
Различают дифференциальный и интегральный температурные дроссель-эффекты. При дифференциальном эффекте Джоуля-Томсона температура изменяется на бесконечно малую величину, а при интегральном - на конечную величину. Если давление газа уменьшается на бесконечно малую величину dp, то происходит бесконечно малое изменение температуры, т.е. dTi = aidpi или
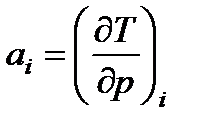 (7.18)
(7.18)
Величина ai называется дифференциальным температурным эффектом Джоуля-Томсона. Значение а, можно определить из уравнения (см. § 5.48)
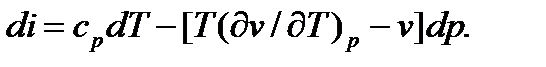
Учитывая, что при дросселировании нет изменения энтальпии (di = 0), получим
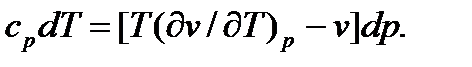
Отсюда
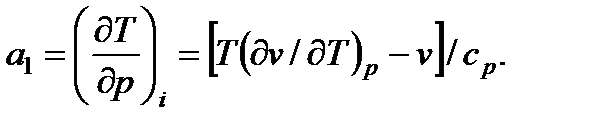 (7.19)
(7.19)
Дроссельный эффект может быть положительным, отрицательным и равным нулю. Положительный дроссель-эффект имеет место в случае, когда при дроселировании температура газа понижается. Отрицательный - когда повышается. В случае неизменности температуры при дросселировании наблюдается нулевой эффект Джоуля-Томсона. Состояние реального газа при дросселировании, когда дроссельный эффект равен нулю, называется точкой инверсии. В этой точке происходит смена знака температурного эффекта. Если температура газа перёд дросселированием меньше температуры инверсии, то газ при дросселировании охлаждается, если больше - то нагревается.
Для нахождения условий, при которых происходит изменение температуры газа или она остается неизменной, необходимо проанализировать уравнение (7.19), записанное в виде
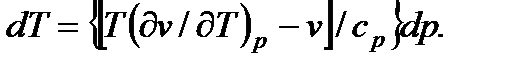 (7.20)
(7.20)
При дросселировании dp < 0, так как давление газа всегда уменьшается. Теплоемкость ср - величина положительная. Отсюда следует, что знак dT
зависит от знака выражения 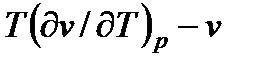 и всегда ему противоположен.
и всегда ему противоположен.
Тогда при 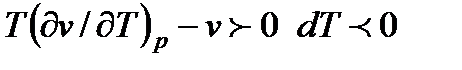 , при
, при 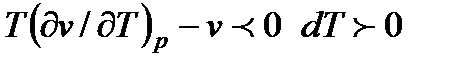 ,
,
при T(dv / dT)p - v = 0 dT = 0. Случай, когда dT = 0 можно использовать для
получения температуры инверсии Тнн.
T(dv/dT)р -v = 0, Tнн=v/(dv/dT)р .
Последнее выражение называется уравнением кривой инверсии (кривой, на которой дроссельный эффект равен нулю).
Интегральный эффект Джоуля-Томсона определяется в результате интегрирования уравнения (7.20)
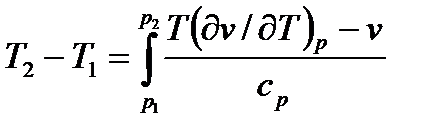 .
.
ГАЗОВЫЕ СМЕСИ
В технике довольно часто приходится иметь дело с газообразными веществами, представляющими механическую смесь отдельных газов, по своим свойствам приближающуюся к идеальным газам.
Например, атмосферный воздух представляет газовую смесь, включающую азот, кислород, углекислый газ, водяные пары и ряд других газов. Определение параметров необходимо для решения многих практических задач.
Газовой смесью называется смесь отдельных газов, химически не реагирующих между собой, т.е. каждый газ в смеси полностью сохраняет все свои свойства и занимает весь объем смеси. Давление, которое создают молекулы каждого отдельного газа смеси, при условии, что этот газ находится один в том же количестве в том же объеме и при той же температуре, что и в смеси, называется парциальным (частичным) давлением.
Будем считать, что каждый отдельный газ смеси подчиняется уравнению (2.7), т.е. является идеальным газом. Поэтому параметры газовой смеси так же могут быть вычислены по уравнению Клапейрона
pV = mRT,
где все величины в этом уравнении относятся к смеси газов.
Согласно закону Дальтона общее давление смеси идеальных газов равно сумме парциальных давлений газов, входящих в смесь
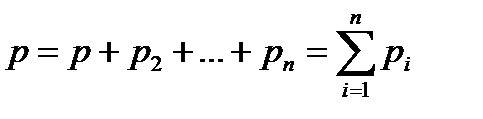
где р- давление смеси; 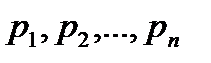 парциальные давления отдельных газов смеси.
парциальные давления отдельных газов смеси.
Газовая смесь может быть задана массовыми, объемными и молярными долями.
Массовая доля - отношение массы каждого отдельного газа к суммарной массе смеси
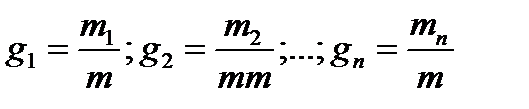
где g1, g2,…, gn - массовые доли отдельных газов; m- суммарная масса всей
смеси
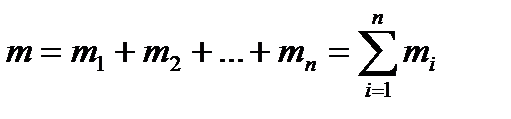
Сумма массовых долей равна единице
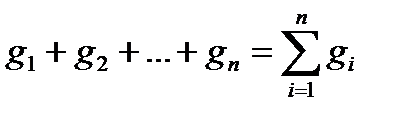
Объемная доля - отношение парциального (приведенного) объема каждого газа к общему объему смеси
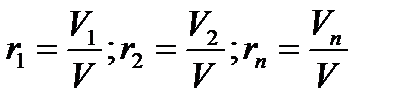
где r1, r2,…, rn объемные доли;V1, V2,…,Vn - парциальные объемы каждого
газа; V- объем смеси газов.
Парциальный объем - это объем, который занимал бы газ, если бы его давление и температура равнялись параметрам смеси газов.
Парциальный объем каждого газа при постоянной температуре находится по закону Бойля-Мариотта
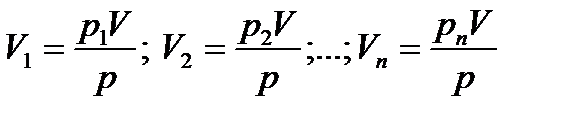
Сложив эти уравнения почленно, получим, что сумма парциальных объемов равна объему смеси (закон Амага)
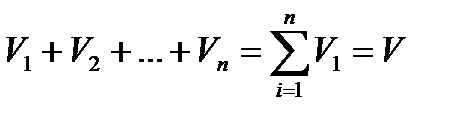
Если сложить объемные доли, то получим
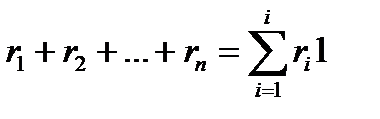
Из закона Бойля-Мариотта (при постоянной температуре) следует pi /p-Vi /V.Отсюда
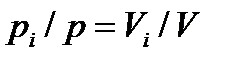
Или
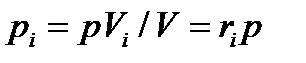
Последняя формула позволяет определять парциальные давления компонентов смеси, если известен ее объемный состав.
Задание смеси молярными долями заключается в следующем. Сначала находим количество молей каждого компонента смеси по соотношениям
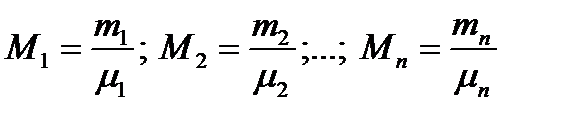
где M1, M2, … , Mn - количество молей каждого компонента; µ1, µ2,…, µn молекулярные веса соответствующих компонентов смеси.
Отсюда вся газовая смесь будет содержать Ммолей
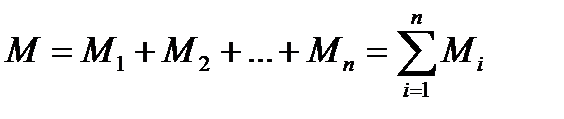
Мольные доли yi (i=1,2,3,…,n) находятся в виде отношений
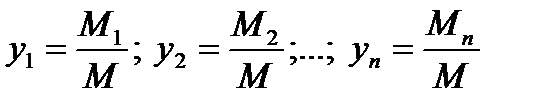
Очевидно, что
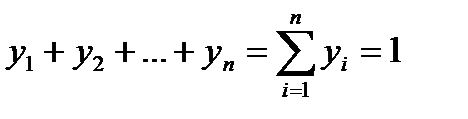
Так как М = m/µ,то молекулярный вес смеси µбудет определяться по формуле
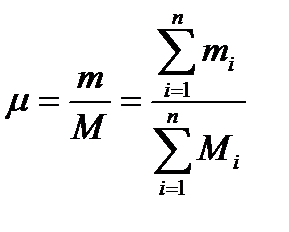
Полученное значение называется средним кажущимся значением молекулярного веса смеси. Знание молекулярного веса позволяет по формуле (2.9а) R=8.3143/µ находить газовую постоянную смеси R(ниже будет приведена формула для определения µпо известной R).
По закону Авогадро мольные объемы различных газов при одинаковых давлениях и температурах равны (в равных объемах различных газов содержится одинаковое количество молекул). Отсюда для i-го газа смеси справедливо соотношение
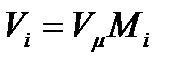
где Vµ - объем, занимаемый одним молем газа.
Для всей смеси получим
V=VµM.
Отсюда
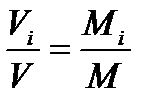
или
yi=ri
Следовательно, мольные и объемные доли численно равны между собой.
Выведем формулу для определения молекулярного веса смеси по ее объемному составу. Из предыдущего для i-го компонента можно записать
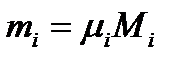
или для всей смеси
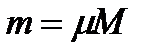
Отсюда следует
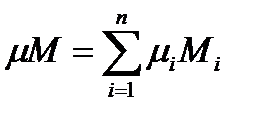
или
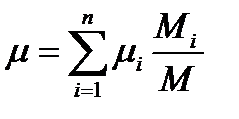
Учитывая, что Mi /M=ri получим
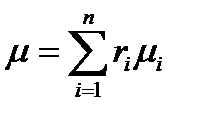
Заменяя в последнем уравнении молекулярные веса их плотностью (на основании закона Авогадро), получим
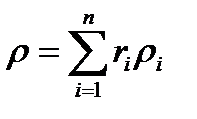
так как
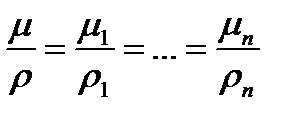
В случае, когда газовая смесь задана массовым составом, то из уравнения состояния
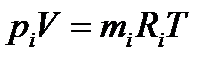
Отсюда
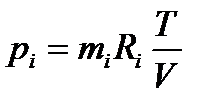
Для давления всей смеси получим формулу
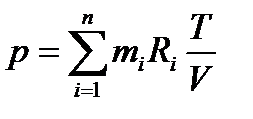
Или
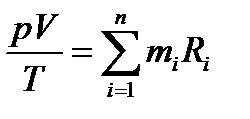
Учитывая, что pV=mRT, получим
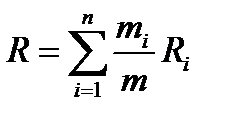
По известной газовой постоянной смеси, используя формулу (2.9а), можно найти молекулярный вес смеси.
Глава 8
Дата добавления: 2016-06-05; просмотров: 14645;











