Электропроводность собственных полупроводников

Рассуждения, приведенные выше при выводе формулы для электропроводности металла, справедливы как для электронов проводимости, так и для дырок. Для дырочного полупроводника удельная электропроводность дырок

, (4.13)

где p - концентрация дырок.

В общем случае удельная электропроводность определяется как электронами, так и дырками:

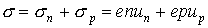. (4.14)

Электронная составляющая проводимости определяется первым слагаемым в формуле (4.14), второе слагаемое связано с дырочной проводимостью полупроводника.

Величина удельной проводимости полупроводника и ее температурная зависимость зависят от концентраций носителей (электронов и дырок) и их подвижностей, которые в свою очередь определяются типом полупроводника. В собственном полупроводнике концентрации электронов и дырок одинаковы (n = p = n_i = p_i, где n_i и p_i - собственные концентрации носителей). Тогда удельная электропроводность _c собственного полупроводника будет равна

. (4.15)

Электропроводность собственного полупроводника называют собственной электропроводимостью и обозначают обычно _с.

Концентрация электронов в собственном полупроводнике определяется выражением (3.17). Логарифмируя это выражение, получим

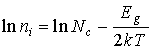. (4.16)

Первое слагаемое в этом выражении слабо зависит от температуры, поэтому график зависимости 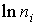от 1/T представляет собой прямую линию (рис. 4.4).

Рис. 4.4. Температурная зависимость концентрации носителей заряда в собственном полупроводнике

Таким образом, концентрация носителей заряда в собственных полупроводниках зависит от ширины запрещенной зоны E_g и температуры Т. Для германия, например, E_g = 0,72 эВ (при T = 300 K) и концентрация собственных носителей заряда при комнатной температуре составляет приблизительно 2,510¹⁹ м^-3. Для кремния соответственно E_g = 1,1 эВ и n_i = 1,5 10¹⁶ м^-3.

Другим фактором, влияющим на температурную зависимость электросопротивления собственных полупроводников, является подвижность носителей заряда. Температурная зависимость подвижности носителей заряда в полупроводниках определяется механизмами рассеяния носителей в кристалле. В идеальном полупроводнике с собственной проводимостью подвижность определяется рассеянием на тепловых колебаниях решетки (фононах), поскольку идеальный собственный полупроводник - это полупроводник без примесных атомов и рассеяние на примесных атомах отсутствует. При анализе температурной зависимости подвижности необходимо учитывать, является ли газ носителей невырожденным или вырожденным при данных условиях. Теоретические расчеты и оценки температурной зависимости подвижности носителей заряда в кристаллах при различных условиях схематически представлены на рис. 4.5.

В области высоких температур подвижность обратно пропорциональна Т^3/2 для невырожденного газа носителей и обратно пропорциональна Т для вырожденного газа носителей. В области низких температур подвижность невырожденного газа носителей пропорциональна Т^3/2 и не зависит от температуры для вырожденного газа носителей. В любом случае степенная зависимость от температуры подвижности носителей значительно слабее экспоненциальной температурной зависимости концентрации носителей заряда в собственных полупроводниках. Вследствие этого температурную зависимость удельной электропроводности собственных полупроводников согласно выражению (4.15) в первом приближении можно представить в виде

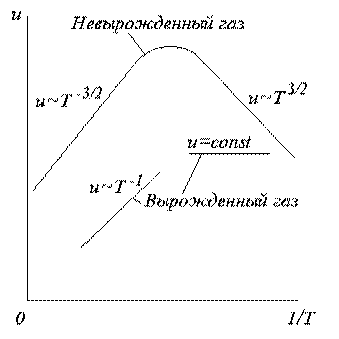Рис. 4.5. Температурные зависимости подвижности невырожденного и вырожденного газа носителей

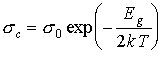, (4.17)

где ₀ - значение удельной электропроводности полупроводника при T 

Логарифмируя последнее равенство, получим

. (4.18)

Таким образом, график зависимости от 1/Т представляет собой прямую линию, тангенс угла наклона которой к оси абсцисс пропорционален ширине запрещенной зоны. Это обстоятельство позволяет использовать данные по температурной зависимости электропроводности для нахождения ширины запрещенной зоны полупроводников.