II. Электропроводность.

В отсутствии внешнего электрического поля электроны участвуют в тепловом хаотическом движении со средней тепловой скоростью <u>, при этом все направления равноправны. Так как в металлах разрешенная зона заполнена не полностью, то даже слабое электрическое поле способно вызвать переход электронов на вышележащие свободные уровни. Переходы в нижележащие уровни невозможны, так как эти состояния заняты. Это приводит к тому, что электроны приобретают преимущественное направление скорости против внешнего электрического поля. Однако ускоряться могут не все электроны, а лишь небольшая часть электронов, имеющих энергии близкие к энергии Ферми (E_F ± kT). Поэтому можно считать, что все свободные электроны в металле имеют скорость, соответствующую энергии Ферми v_эл = v_F. Под действием приложенного электрического поля напряженностьюE электрон с эффективной массой m* и зарядом e за время между соударениями τ приобретает средний импульс p и среднюю дрейфовую скорость v_др:

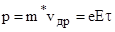
Отсюда v_др = eEτ/m*. Время свободного пробега τ можно определить через длину свободного пробега ℓ_эл электрона τ=ℓ_эл/v_F.

Плотность электрического тока при концентрации электронов n равна

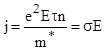
Коэффициент пропорциональности σ между j и E представляет собой удельную электропроводность. Удельное сопротивление металла есть обратная величина

.

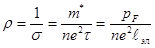Как видно оно зависит от импульса Ферми p_F, концентрации электронов n и длины их свободного пробега ℓ_эл. При изменении температуры энергия Ферми в металлах изменяется столь незначительно, что этим изменением можно пренебречь. Соответственно остаются неизменными v_F и p_F. Концентрация свободных электронов n также изменяется очень незначительно. Поэтому электропроводность определяется в основном средней длиной свободного пробега.

Квантовые представления приводят к следующему выражению для удельной электропроводности металла

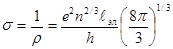(1)

где r – удельное сопротивление, e - элементарный заряд, n – концентрация электронов, ℓ_эл – средняя длина свободного пробега электрона, h – постоянная Планка.

Если считать, что каждый атом в металле поставляет один свободный электрон, то концентрация свободных электронов равна концентрации атомов и может быть рассчитана по формуле

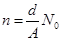, (2)

где d – плотность металла; А – атомная масса; N₀– число Авогадро.

В электропроводности под длиной свободного пробега понимается длина, на которой электрон полностью теряет свою скорость направленного движения, обусловленную приложенным электрическим полем. Это означает, что импульс электрона (приблизительно равный p_F) должен измениться до нуля, т.е. изменение практически равно самому импульсу. Поэтому основное влияние на длину свободного пробега будут оказывать взаимодействия с препятствиями, способными обеспечить такое изменение импульса электрона.

1. Рассеяние

При T>Θ, учитывая зависимости ℓ_эл и n от температуры в этом диапазоне температур, для удельного сопротивления металла, обусловленного рассеянием на фононах, получим линейную зависимость ρ_ф от температуры:

.

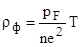Импульс фононов при этом достаточно велик, чтобы обеспечить изменение импульса электрона от p_F до нуля: ∆p_эл ≈ p_эл ≈ p_ф = kΘ/v_зв.

При T<Θ эта зависимость нарушается. При понижении температуры рождается все меньше фононов, их энергии становятся все меньше. Импульс фонона мал и его недостаточно для остановки электрона, т.к. изменение импульса электрона не может превышать импульс фонона. Нужны многократные столкновения с фононами, прежде чем импульс электрона сможет заметно измениться. Кроме того, уменьшаются амплитуды колебаний атомов, а соответственно и эффективное сечение рассеяния. Теоретический расчет показывает в этой области степенную зависимость удельного сопротивления от температуры : ρ_ф ~ T⁵ . Экспериментальные значения показателя степени лежат в пределах от 4 до 6. Температурный интервал, в котором наблюдается такая зависимость, обычно очень небольшой.

Сопротивление, обусловленное рассеянием на дефектах, ρ_ост не зависит от температуры и называется остаточным сопротивлением.

2. Электропроводность в широком диапазоне температур

Для металлов справедливо правило Матиссена: полное сопротивление металлов суть сумма сопротивления, обусловленного рассеянием электронов на тепловых колебаниях решетки (фононах), и остаточного сопротивления, обусловленного рассеянием на статических дефектах структуры ρ = ρ_ф + ρ_ост. Исключение из этого правила составляют сверхпроводящие металлы, в которых остаточное сопротивление равно нулю и полное сопротивление исчезает ниже некоторой критической температуры.

Рис. 1. Зависимость удельного сопротивления металла от температуры.

В зависимости удельного сопротивления металла от температуры в широком диапазоне температур (рис. 1) можно выделить несколько характерных участков:

I – наблюдается сверхпроводимость у чистых металлов и остаточное сопротивление у металлов с дефектами;

II – переходная область с сильной степенной зависимостью ρ ~ T^m , где показатель степени убывает от m=5 до m=1 при T=Θ;

III – линейный участок, у большинства металлов простирается до температур, порядка ⅔Θ, т.е от комнатных до близких к точке плавления;

IV – вблизи точки плавления начинается отклонение от линейной зависимости, вызванное ангармоничностью колебаний кристаллической решетки.

В области линейной зависимости удельного сопротивления от температуры справедливо выражение ρ = ρ₀[1+α(T-T₀)], где Т₀ – начальная температура, ρ₀ – удельное сопротивление при Т₀, α – температурный коэффициент удельного сопротивления, показывающий насколько изменяется удельное сопротивление при изменении температуры на один Кельвин.