Вывод уравнения ВАХ для прямого тока полупроводникового диода в зависимости от температуры.

Рассмотрим задачу о нахождении уравнения ВАХ для прямого тока полупроводникового диода. Эмпирическое уравнение, полученное мной выше, имеет вид:

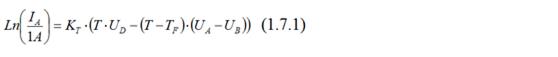
С использованием СТЭ-потенциалов оно было приведено к виду:

где ΔF₁, ΔF₂ - СТЭ-потенциалы.

При помощи теории зарядов-энергий выведем это уравнение ВАХ полупроводникового диода. Полупроводниковый диод представляет собой термопару, в которой электроны при прямом токе совершают переход из зоны N в зону P. Такой переход сопровождается выделением энергии, а обратный переход невозможен, так как требует дополнительной энергии для электронов.

Условия задачи следующие. Через две различные зоны полупроводников протекает ток I_A. Изменим единицу измерения тока - так как существует квант электрического заряда «электрон», то единицу измерения тока можно сделать штучной (штука в секунду), для чего ток в Амперах следует поделить на заряд электрона в Кулонах:

где e = 1.6•10^-19 Кл - заряд электрона.

T_C – температура окружающей среды.

U_A – напряжение, приложенное к PN-переходу.

На переходе из N в P существуют СТЭ-потенциалы. В лабораторной установке происходит термоэлектрический процесс, в котором есть приложенные СТЭ-потенциалы и есть протекающий ток, величина которого в цепи постоянна. СТЭ-потенциалы образуются из следующих приложенных температур и напряжений:

T₁₀ = T_F - входная температура зоны P,

T₁₁ = Т_C - выходная температура зоны P,

T₂₀ = 0 - входная температура зоны N,

T₂₁ = T_C - выходная температура зоны N,

U₁₀ = U_B - входное напряжение зоны P,

U₁₁ = U_A - выходное напряжение зоны P,

U₂₀ = 0 - входное напряжение зоны N,

U₂₁ = U_D - выходное напряжение зоны N,

где T_F, U_D, U_B – параметры эмпирической модели (см. выше). Эти параметры приведены, чтобы показать связь с опытными данными. В выводе уравнения ВАХ для прямого тока диода в данной главе они не используются.

Отсюда можно найти все разности потенциалов:

ΔT₁ = T₁₁ - T₁₀ - входная разность температур,

ΔT₂ = T₂₁ - T₂₀ - выходная разность температур,

ΔU₁ = U₁₁ - U₁₀ - входная разность электрических потенциалов,

ΔU₂ = U₂₁ - U₂₀ - выходная разность электрических потенциалов.

Через переход протекает ток ΔI_A = I_A. Здесь потенциал тока рассматривается относительно вакуума. Рассмотрим электрический ток при переходе из среды в среду (см. рис. 1.8.1). Такой переход создаёт условия для возникновения флуктуационного тока. При переходе из среды в среду на участках тока создаётся разность СТЭ-потенциалов:

ΔF₁ = ΔT₁ * ΔU₁

ΔF₂ = ΔT₂ * ΔU₂

ΔF_Σ = ΔF2 - ΔF1

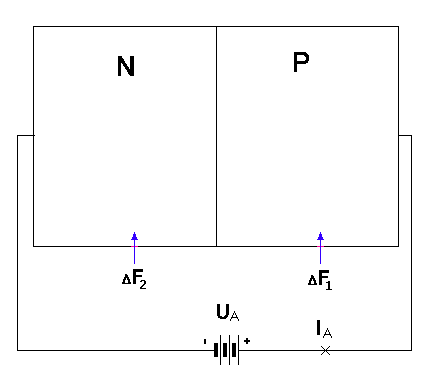
Рис. 1.8.1. Схема исследования PN-перехода с приложенными СТЭ-потенциалами.

Найдём перенос полного флуктуационного тока электрическим током – это полный флуктуационный ток в данном процессе:

Соотношение (1.8.3) выведено на основании закона (1.7.35). Выражение (1.8.3) показывает, что электрический ток I_A является проводимостью для флуктуационного тока G_Σ.

В то же время полный флуктуационный ток можно вычислить, принимая во внимание тот факт, что каждая частица тока способна переносить некоторую долю флуктуационного тока, характеризуемого как удельную энергию теплообмена, приходящийся на единицу заряда. Обозначим удельную энергию теплообмена анодного тока на единицу электрического заряда как ΔF_Ед. Флуктуационный ток единичной части электрического тока I_АЕ , вычисленный через удельную энергию теплообмена на единицу электрического заряда, имеет вид:

Полный флуктационный ток можно вычислить из единичных токов, если просуммировать все флуктационные токи на единицу электрического заряда, приходящиеся на единичные электрические токи. Флуктуационный ток G_Σ в данном случае будет представлять собой интеграл от выражения G_Ед , взятый по электрическому току.

Пусть электрический ток достигает величины I_А. Его можно измерять в различных единицах - переведём единицы измерения тока в «штуки в секунду» (см. выше):

где e = 1.6•10^-19Кл - заряд электрона.

Далее переведём ток одного электрона в секунду:

Тогда нижний предел интегрирования будет иметь вид единичного тока I₁ = I_Ne = 1 шт./сек., а верхний предел интегрирования - значение I₂ = I_NIa.

ΔF_Ед = ΔT₃*ΔU₃- удельная энергия теплообмена на единицу электрического заряда при протекании единичного тока. Также ΔF_Ед имеет физический смысл некоторого СТЭ-потенциала, постоянного в данном процессе.

Если полный ток равен N штук в секунду, то

Из выражения (1.8.7) можно найти суммарный флуктуационный ток методом итегрирования:

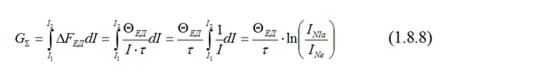
Выражение I_NIa / I_Ne переведём обратно в Амперы:

Теперь мы имеем два выражения (1.8.3) и (1.8.8) для G_Σ, приравняем их:

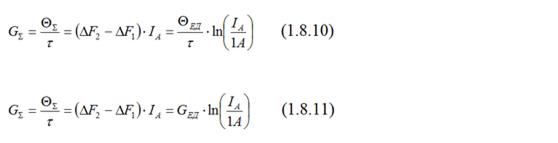
Так как флуктуационный ток имеет в своём составе частицы с электрическим зарядом, то совместно с флуктуационным током возникает электрический ток. На единичный электрический ток всегда приходиться некоторая доля флуктуационного тока, равная G_Ед, где G_Ед - некоторый параметр, определяющий флуктуационный ток, переносимый единичным электрическим током в условиях флуктуационного тока. Иначе говоря, можно записать:

Далее из (1.8.10) следует:

где ΔF_Ед – некоторый СТЭ-потенциал, постоянный в данном процессе. Отсюда:

Если принять:

То получим искомое выражение:

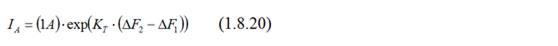
Формула (1.8.20) совпадает с (1.8.1). Таким образом, мы строго вывели уравнение ВАХ полупроводникового диода, которое не противоречит эксперименту.