Движения в процессе резания

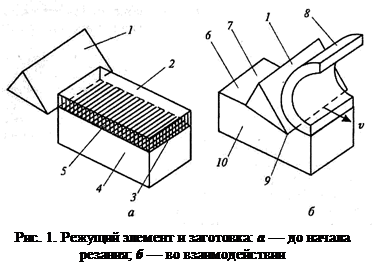На схеме резания (рис. 1) показаны: предмет труда до обработ­ки — заготовка 4 и после обработки резанием — деталь 10, а также режущий элемент 1 рабочего орудия во взаимодействии с заготов­кой. В процессе резания исходная обрабатываемая поверхность 2 подлежит трансформации в обработанную поверхность 6 детали. Для этого с заготовки должна быть удалена часть материала — припуск 3. Режущий элемент воздействует на заготовку прежде всего лезвием — активным ребром клина с режущей кромкой 9, фор­мирующим новую поверхность в заготовке — поверхность реза­ния 7. Часть припуска, заключенная между двумя смежными по­верхностями резания, составляет срезаемый слой 5. Срезаемый слой, удаленный с заготовки лезвием и получивший объемную деформацию (изменение формы и размеров), называется струж­кой 8. В простейшем случае припуск совпадает со срезаемым сло­ем, а поверхность резания — с обработанной поверхностью де­тали.

Рассмотрим элементарную технологическую задачу, решаемую резанием. Пусть с заготовки для получения плоской поверхности требуется удалить припуск. При небольших размерах припуска ре­зец снимает его за один проход. Однако при значительных разме­рах припуска такое решение неудовлетворительно: либо действу­ющие со стороны заготовки на резец большие силы сопротивле­ния резанию приведут к чрезмерной деформации резца и его поломке, либо качество обработанной поверхности будет недо­пустимо низким.

В этом случае задача решается послойным удалением припуска: сначала резцу сообщают движение резания, в результате которого отделяется первый слой и на заготовке формируется поверхность резания. Затем резец возвращают в исходное положение и, сооб­щая ему движение, перпендикулярное движению резания, пере­мещают в новое исходное положение, после чего осуществляют новое движение резания и срезают второй слой. Рассмотренные движения могут быть приданы как резцу, так и заготовке.

Стружка — это часть материала, срезанная с обрабатываемого объекта за один проход резца. В случае обработки на ножницах, высечках и штампах отделяемые части материала носят название срезков. Поверхность, образованная после отделения стружки, называется поверхностью резания.

Главное движение — это простое движение лезвия, обеспечива­ющее удаление одного срезаемого слоя. Движение подачи — про­стое движение лезвия, необходимое для последовательного удале­ния ряда срезаемых слоев.

В процессе резания может быть одно главное движение и одно или несколько движений подачи. Главное движение и движение подачи составляют основу хода резания, т. е. комплекса движений лезвия, обеспечивающих образование одной поверхности резания. Движения хода резания (главное и подачи) могут происходить не­прерывно или прерывисто, одновременно или попеременно. Если одновременно с главным движением совершается еще хотя бы одно движение, каждая точка лезвия при резании совершает сложное движение.

Движением резания принято называть сложное движение лезвия при образовании поверхности резания.

Для многократного повторения ходов резания лезвие должно воз­вращаться в положение, исходное для начала очередного хода реза­ния. Совокупность движений возврата составляет холостой ход.

Каждое движение характеризуется траекторией движения точ­ки режущей кромки и законом движения этой точки вдоль траек­тории. В процессах резания древесины траекториями простых дви­жений являются, как правило, прямая и окружность.

Скорость сложного движения определяется как геометрическая сумма скоростей одновременно совершаемых движений.

Так, скорость движения резания v_e в большинстве станочных процессов складывается из скорости главного движения v и ско­рости подачи v_s: v_e = v + v_s. Учитывая, что скорость главного дви­жения, как правило, во много раз превосходит скорость подачи и других движений хода резания, для практических целей можно считать траекторию резания совпадающей с траекторией главного движения и принимать v_e ≈ v, оговаривая при этом вносимую по­грешность.

Геометрия резца

При анализе процесса резания можно ограничиться рассмотре­нием активной части режущего элемента — лезвия. Под геометри­ей лезвия понимают совокупность характеристик его формы и рас­положения в пространстве. Пусть клиновидное лезвие 3 прошло в заготовке 4 некоторый путь (рис. 2, а), образуя стружку 2. В режу­щей части клина можно выделить следующие элементы: пере­днюю поверхность Аγ, контактирующую со срезаемым слоем 1 и стружкой; заднюю поверхность Аα, примыкающую к режущей кромке 5 и обращенную к формируемой в заготовке поверхности резания Р_п, режущую кромку 5, образованную пересечением пе­редней и задней поверхностей. В более сложных случаях полуза­крытого (рис. 2, б) и закрытого (рис. 2, в) резания следует разли­чать режущие кромки: главную АВ и вспомогательные ВС и AD. Со­ответственно у лезвия выделяют задние поверхности: главную, при­мыкающую к главной режущей кромке, и вспомогательные, при­мыкающие к вспомогательным режущим кромкам. Главной счита­ется режущая кромка, формирующая большую сторону сечения срезаемого слоя. Вспомогательные режущие кромки формируют мень­шие стороны. Элемент сопряжения главной и вспомогательной ре­жущих кромок называют вершиной лезвия (точки А и В).

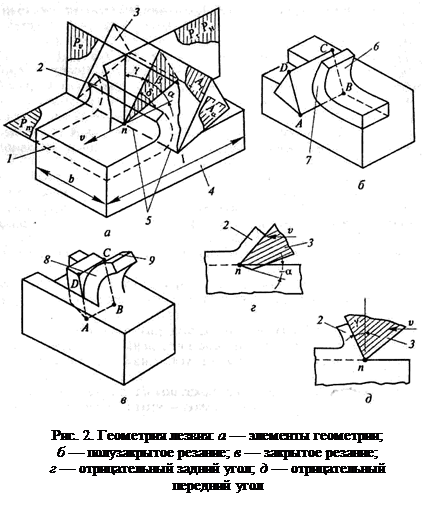Передняя и задняя поверхности могут иметь любую форму (вог­нутую, выпуклую или ломаной линии). Сопряжение режущих кро­мок может быть радиусным или точечным.

Положение режущих кромок и поверхностей лезвия в простран­стве определяет угловые параметры процесса резания. Для опреде­ления углов установлены исходные координатные плоскости: ос­новная плоскость и плоскость резания (рис. 2, а).

Основная плоскость P_v — координатная плоскость, про­веденная через рассматриваемую точку (например, п) режущей кромки перпендикулярно направлению скорости главного v или результирующего v_e движения резания в этой точке.

Плоскость резания Р_п — координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная основной плоскости P_v.

Дополнительными координатными плоскостями являются главная и нормальная секущие плоскости. Главная секу­щая плоскость Р_τ — координатная плоскость, перпендикулярная линии пересечения основной плоскости P_v и плоскости резания Р_п. Нормальная секущая плоскость Р_H — плоскость, перпендику­лярная режущей кромке в рассматриваемой точке (на рис. 2 плос­кости Рτ и Р_H совпадают).

Выделяют также рабочую плоскость P_s, в которой рас­положены векторы скоростей главного движения резания v и дви­жения подачи v_s (показана на рис. 3, д).

Угловые параметры резания характеризуются главными (при главной режущей кромке) и вспомогательными (при вспомога­тельной режущей кромке) углами, углом наклона главной режу­щей кромки.

Различают следующие углы (показаны на рис. 2, а для главной режущей кромки): γ — передний угол — угол в секущей плоскости Р_τ между передней поверхностью лезвия А_γ и основной плоско­стью P_v; α — задний угол — угол в секущей плоскости Р_τ между задней поверхностью лезвия А_α и плоскостью резания Р_n; β — угол заострения — угол в секущей плоскости Р_τ между передней А_γ и задней А_α поверхностями лезвия.

Сумма заднего угла α и угла заострения β называется углом резания δ: δ = α + β. Между главными углами существует про­стейшая связь:

α + β + γ = 90° (1)

В случае, когда задняя поверхность лезвия оказывается под по­верхностью резания (т. е. когда угол α прочерчивается в пределах контура лезвия), задний угол считают отрицательным (рис. 2, г). Передний угол у также считают отрицательным, если он про­черчивается в пределах контура лезвия (рис. 2, д). С учетом зна­ков углов α и γ равенство α + β + γ = 90° справедливо во всех слу­чаях.

Главные углы могут рассматриваться в инструментальной, ста­тической и кинематической системах координат (ГОСТ 25762—83).

Инструментальная система координат — прямоугольная систе­ма координат с началом в вершине лезвия, ориентированная от­носительно геометрических элементов режущего инструмента, принятых за базу (рис. 3, а). Применяется для описания конструк­ции режущего элемента или инструмента в целом, например при конструировании и изготовлении.

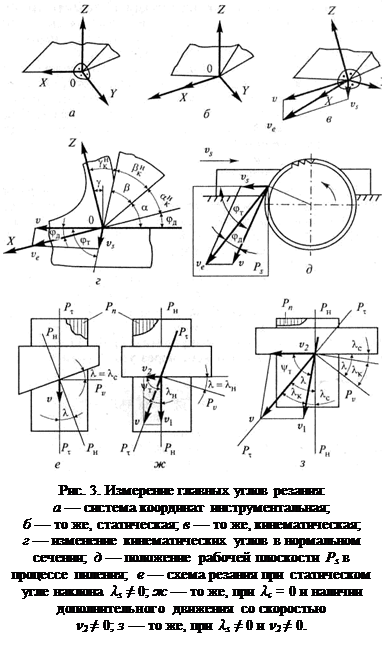Статическая система координат — прямоугольная система ко­ординат с началом в рассматриваемой точке режущей кромки, ориентированная относительно направления скорости главного движения резания v. Определяет геометрию лезвия и его положе­ние относительно заготовки в статике, т. е. без учета параметров главного движения и движения подачи (рис. 3, б).

Кинематическая система координат — прямоугольная система координат с началом в рассматриваемой точке режущей кромки, ориентированная относительно направления скорости результи­рующего движения резания v_e (рис. 3, в). Фактические величины углов в процессе резания находят отражение только в кинемати­ческой системе координат.

Рассмотрим кинематические углы подробнее. На рис. 3, г пока­зано лезвие, перемещающееся относительно заготовки с резуль­тирующей скоростью v_e, причем вектор v_e совпадает с нормалью к режущей кромке (в этом случае режущая кромка расположена в основной плоскости P_v). Тогда на рис. 3, г плоскость XZ совпадает с плоскостями главной секущей Р_х и нормальной секущей Р_н. По­ложение плоскости резания Р_п совпадает с осью X, а положение основной плоскости P_v — с осью Z. По определению находим кинематические углы для главной режущей кромки (главные ки­нематические углы): α_k^H — задний, β_k^H — заострения, γ_k^H — перед­ний (буква «н» в обозначении напоминает о том, что режущая кромка нормальна к векторам v_e и v).

Связь между кинематическими углами а^н_к, β_k^H, γ_k^H и статичес­кими углами α, β, γ устанавливают через угол движения φ_Д (см. рис. 3, г, д):

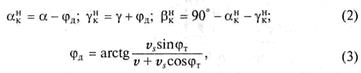
где φ_T — технологический угол между векторами скоростей v и v_s, (задан схемой обработки).

При φ_T = 90° формула для угла φ_Д упрощается: φ_Д = arctg (v_s /v).

В практике резания древесных и облицовочных материалов рас­пространены случаи, когда вектор скорости главного v или ре­зультирующего движения v_e не совпадает с нормалью к режущей кромке, т.е. случаи, когда режущая кромка наклонена к основной плоскости P_v на некоторый угол λ (рис. 3, е, ж, з; на них заготов­ка и резец показаны в плане).

Угол наклона режущей кромки λ следует определять как сумму статического угла наклона λ_с (см. рис. 3, е, з) и кинематического угла наклона λ_к (см. рис. 3, ж, з). Статический угол λ_с задается установкой лезвия в статической системе координат. Кинемати­ческий угол λ_к появляется в схемах резания, где скорость главного движения v задается как геометрическая сумма собственно главного движения со скоростью v_x и дополнительного движения вдоль режущей кромки со скоростью v₂ (см. рис. 3, ж, з):

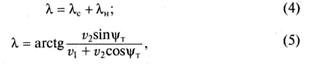
где ψ_т — технологический угол между векторами скоростей v_x и v₂ (задан схемой обработки).

При ψ_т = 90° формула для угла λ_к упрощается: λ_к = arctg (v₂/v₁).

Таким образом, в общем случае (при учете движения подачи и наклона режущей кромки к основной плоскости) кинематические углы равны:

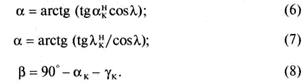
Технолог должен знать закономерности изменения статических углов резания при работе инструмента и уметь учитывать эти изме­нения при разработке требований к режущему инструменту и выбо­ре режима резания. Значения наилучших углов а_к, р_к, "к_к выбирают по справочной литературе. Затем по соотношениям (4)...(8) следу­ет определить кинематические углы, приведенные к нормальному сечению: ос" (3”, у_к'. Далее по формулам (2) и (3) установить стати­ческие углы лезвия а, (3, у. Именно эти статические углы контроли­руют измерением их в нормальной секущей плоскости Р_н.

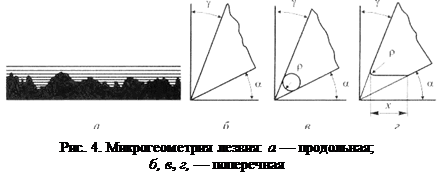Режущая кромка лезвия представляет собой переходную кривую поверхность, соединяющую переднюю и заднюю поверхности. Ха­рактеристики переходной поверхности объединяются в понятие микрогеометрии лезвия. Различают продольную (вдоль кромки) и поперечную (в нормальном сечении) микрогеометрии. Продольная микрогеометрия (рис. 4, а) характеризуется «шероховатостью» ре­жущей кромки. Поперечная микрогеометрия характеризуется профи­лем лезвия в нормальном сечении. Идеальный геометрический клин был бы идеально острым (рис. 4, б). Кромка реального лезвия, прора­ботавшего некоторое время, может быть принята за дугу окружности радиуса р (рис. 4, в). Радиус ρ называют радиусом округления режу­щей кромки. В начальном состоянии режущие элементы инструмента для резания древесины характеризуются показателями: шероховатость кромки (средняя высота наибольших неровностей профиля) 4... 5 мкм, радиус округления 2...5 мкм.

Во время резания в результате сложных физико-химических процессов происходит износ лезвия — изменение геометрии и мик­рогеометрии его элементов. Следствием износа является затупле­ние лезвия, т. е. потеря им остроты, режущих свойств. Затупление лезвия характеризуют различными параметрами. В большинстве случаев резания натуральной древесины ограничиваются величи­ной радиуса округления ρ, так как этот параметр оказывает глав­ное влияние на силы резания и стружкообразование. В тех случаях, когда происходит интенсивный износ лезвия по задней поверхнос­ти, параметром затупления может служить величина износа по зад­ней грани — ширина фаски х (рис. 4, г).