Энтропия источника непрерывных сообщений

Рассмотрим источник непрерывных сообщений, на выходе которого в каждый момент времени 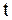появляются сигналы 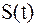. Эти сигналы с бесконечно малой вероятностью могут принимать бесконечное множество значений.

Если бы сообщения могли передаваться по каналам абсолютно точно без искажений, то они содержали бы неограниченное количество информации. На самом деле из-за наличия помех и искажений количество информации, получаемой от такого источника, следует определять как разность энтропии до и после получения информации. Эта разность, в отличие от абсолютной величины энтропии источника непрерывных сообщений, имеет конечную величину. Для её нахождения обобщим рассмотренное ранее понятие энтропии источника дискретных сообщений на случай непрерывных сообщений, воспользовавшись естественным предельным переходом.

Обратимся к сигналу 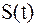, возможные значения которого в момент 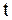характеризуются плотностью распределения вероятностей 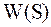, имеющей вид, показанный на рис. 1.

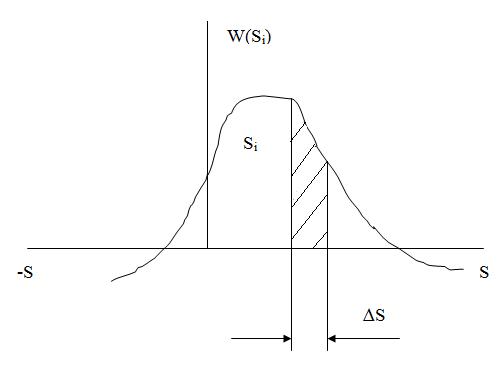
Рис. 1. К определению энтропии источника непрерывных сообщений

Произведём квантование области значений 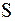с шагом 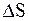( 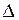– шаг дискретизации непрерывного сигнала во времени). Тогда вероятность попадания некоторого конкретного значения сигнала 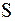в пределы i-го шага квантования будет примерно равна:

;

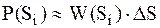(1.1)

При этом приближение тем точнее, чем меньше интервал (шаг квантования) .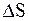

Энтропия такого «дискретного» сигнала равна:

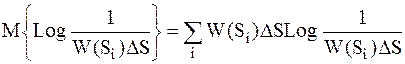;	(1.2)
где		–	математическое ожидание

Перейдем теперь к энтропии непрерывного сигнала, для чего устремим величину 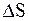к нулю, тогда:

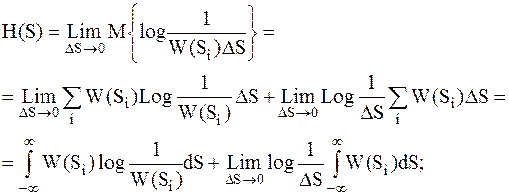
(1.3)

Во втором слагаемом величина 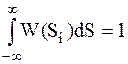по определению, тогда

;

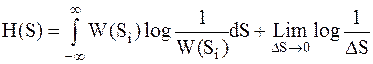(1.4)

В этом выражении первое слагаемое является конечной величиной, которая определяется плотностью распределения 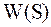. Эту величину называют дифференциальной энтропией сигнала 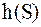. Её обычно рассматривают как некоторую вспомогательную величину при проведении расчётов.

;

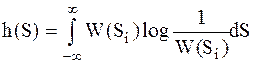(1.5)

Второе слагаемое при ∆S→0 стремится к бесконечности независимо от значений плотности распределения вероятностей сигнала W(S_i). Это означает, что при переходе от дискретной к непрерывной величине энтропия неограниченно возрастает. Это объясняется тем, что при ∆S→0 вероятности попадания в такие малые отрезки становятся бесконечно малыми величинами. В результате неожиданность или непредсказуемость реализаций становится неограниченно большой.

Дифференциальная энтропия гауссовскoго шума с нулевым средним значением и дисперсией 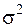в окончательном варианте представляет собой:

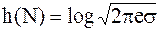;	(1.6)
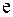
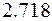
где		=		–	экспонента

Из данного выражения видно, что дифференциальная энтропия гауссовской величины зависит только от значения дисперсии. При этом с ее увеличением дифференциальная энтропия будет монотонно возрастать.

Выводы

1. Из всех видов возможных распределений вероятностей случайных процессов, у которых дисперсия 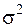является фиксированной величиной, наибольшее значение дифференциальной энтропии имеет гауссовское распределение.