Условная энтропия и ее свойства.

Рассмотрим дискретный канал без памяти, на входе и выходе которого имеются ансамбли дискретных сообщений A и B соответственно. Задача заключается в том, чтобы определить количество информации, переданной по этому каналу. Иначе говоря, необходимо найти информацию, содержащуюся в принятом сообщении 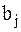при передаче сообщения .

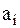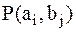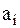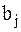Пусть известны – совместная вероятность реализаций и , а также 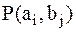– условная вероятность реализации 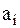, если на выходе канала появилось сообщение 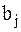. По теореме умножения вероятностей:

;

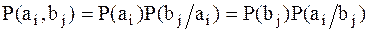(2.1)

Введем понятие условной энтропии, которую определим как математическое ожидание, аналогичное тому, как это было сделано ранее для энтропии источника сообщений:

;

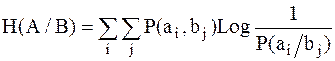(2.2)

Условная энтропия обладает следующими свойствами:

1. 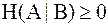, т.е. всегда положительна, что следует из её определения.

2. 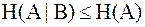, где 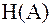- энтропия источника сообщений на входе канала. При этом равенство имеет место в том случае, если 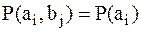при всех 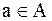и 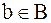, т.е. когда 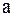и 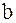взаимно независимы. Это означает, что с получением сообщения 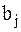никакой информации о сообщении 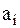не поступает, следовательно, неопределенность не уменьшается. Данная ситуация может соответствовать полной потере информации при передаче из-за помех в канале связи.

Учитывая сказанное, условную энтропию ИДС обычно трактуют как количество информации, которое теряется из-за помех и не поступает получателю. Ясно, что полная потеря информации является крайним случаем и в реальных условиях практически не встречается. Величину 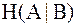называют также надежностью.

Выводы

1. Условная энтропия представляет собой количество информации, которое теряется из-за помех и не поступает получателю.

2. Условная энтропия всегда положительна (ее свойство).