Статическая устойчивость асинхронной машины
Под статической устойчивостью понимается способность асинхронной машины возвращаться в исходный режим после малого возмущения со стороны сети или вала.
Рассмотрим в качестве примера двигательный режим (рис. 4.13). Пусть на ротор действуют электромагнитный момент М и момент сопротивления 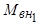 , обусловленный рабочим механизмом. Разность этих моментов определяет динамический момент:
, обусловленный рабочим механизмом. Разность этих моментов определяет динамический момент:
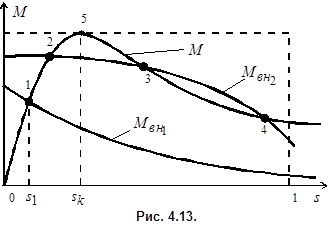
|
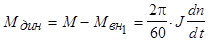 .
.
Принимая во внимание, что 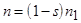 , получим
, получим
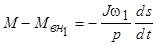 , (4.17)
, (4.17)
где 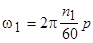 .
.
Задача заключается в том, чтобы при заданных зависимостях 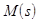 и
и 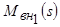 определить устойчивость режима в точке 1. Для решения этой задачи выполним линеаризацию нелинейных функций
определить устойчивость режима в точке 1. Для решения этой задачи выполним линеаризацию нелинейных функций 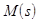 и
и 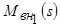 в малой окрестности точки 1:
в малой окрестности точки 1:
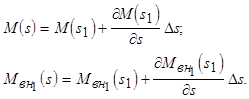
Данные соотношения позволяют записать дифференциальное уравнение (4.17) в малых приращениях:
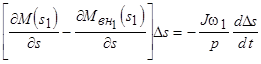 .
.
Это уравнение является линейным, его решение хорошо известно:
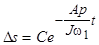 , (4.18)
, (4.18)
где 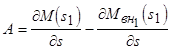 ; С - постоянная, определяемая начальными условиями.
; С - постоянная, определяемая начальными условиями.
Согласно (4.18) асинхронная машина вернется в исходный режим ( 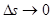 при
при 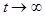 ) после снятия малого возмущения, если
) после снятия малого возмущения, если
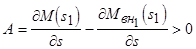 . (4.19)
. (4.19)
Частные производные 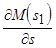 и
и 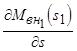 определяют угол наклона касательных к кривым
определяют угол наклона касательных к кривым 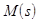 и
и 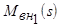 в точке 1. Как следует из рис. 4.13,
в точке 1. Как следует из рис. 4.13, 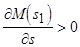 , а
, а 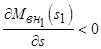 , поэтому
, поэтому 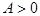 . Следовательно, режим в точке 1 статически устойчив.
. Следовательно, режим в точке 1 статически устойчив.
Если момент сопротивления рабочего механизма определяется кривой 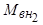 , то согласно критерию статической устойчивости (4.19) в точках 2 и 4 режим работы асинхронного двигателя будет устойчивым, а в точке 3 - неустойчивым. При постоянном моменте сопротивления на валу предельным по устойчивости будет режим в точке 5, соответствующий максимуму электромагнитного момента. Поэтому устойчивой зоной работы двигателя является диапазон скольжений от 0 до
, то согласно критерию статической устойчивости (4.19) в точках 2 и 4 режим работы асинхронного двигателя будет устойчивым, а в точке 3 - неустойчивым. При постоянном моменте сопротивления на валу предельным по устойчивости будет режим в точке 5, соответствующий максимуму электромагнитного момента. Поэтому устойчивой зоной работы двигателя является диапазон скольжений от 0 до 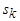 . Кратность максимального момента
. Кратность максимального момента 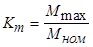 характеризует перегрузочную способность двигателя. Для того, чтобы обеспечить устойчивую работу асинхронного двигателя при возможных колебаниях напряжения сети и момента нагрузки, кратность
характеризует перегрузочную способность двигателя. Для того, чтобы обеспечить устойчивую работу асинхронного двигателя при возможных колебаниях напряжения сети и момента нагрузки, кратность 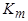 должна быть не ниже
должна быть не ниже 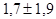 .
.
Дата добавления: 2017-11-21; просмотров: 1607;











