Явления в асинхронной машине при неподвижном роторе
Физическая сущность явлений в асинхронной машине и трансформаторе имеет много общего, поэтому целесообразно начать изучение асинхронных машин с трансформаторного режима при неподвижном роторе ( 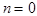 ).
).
Рассмотрим явления в трехфазной асинхронной машине, полагая, что все величины являются синусоидальными функциями времени, а магнитное поле в воздушном зазоре распределено по гармоническому закону. Высшими пространственными гармониками поля пренебрегаем. Обмотку ротора будем считать фазной. Пусть вначале обмотка ротора разомкнута, а обмотка статора включена в сеть на напряжение 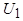 (рис. 4.3, а).
(рис. 4.3, а).
Симметричная система токов 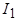 , протекающих по фазам обмотки статора под действием приложенного напряжения
, протекающих по фазам обмотки статора под действием приложенного напряжения 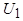 , создает основную гармонику МДС с амплитудой
, создает основную гармонику МДС с амплитудой
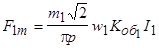 .
.
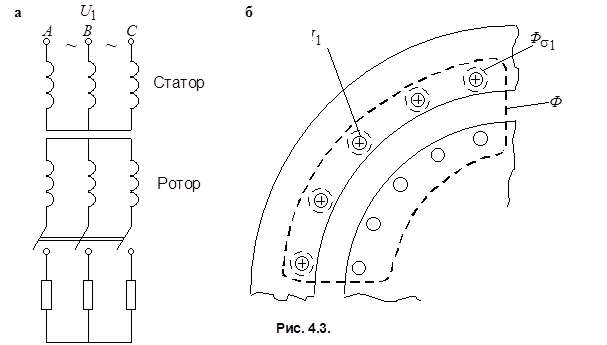
Под действием этой МДС в машине образуется магнитный поток, который обычно разделяют на основной поток Ф, сцепленный с обмотками статора и ротора, и поток рассеяния 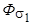 , сцепленный только с обмоткой статора,
, сцепленный только с обмоткой статора,
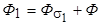 .
.
Основной магнитный поток наводит в обмотках статора и ротора ЭДС
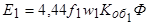 ;
;
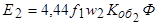 .
.
Для удобства дальнейшего анализа обмотку ротора приведем к обмотке статора. Приведенные величины, как и в трансформаторе, будем обозначать символами со штрихами. Коэффициент приведения по напряжению определяется как отношение ЭДС 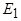 и
и 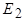 :
:
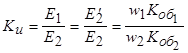 .
.
Появление в формуле для 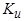 отношения обмоточных коэффициентов обусловлено характером образования магнитного поля в асинхронной машине. В отличие от трансформатора первая гармоника магнитного поля асинхронной машины зависит от конструкции обмотки.
отношения обмоточных коэффициентов обусловлено характером образования магнитного поля в асинхронной машине. В отличие от трансформатора первая гармоника магнитного поля асинхронной машины зависит от конструкции обмотки.
|
ЭДС 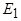 и
и 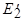 можно также выразить через ток
можно также выразить через ток 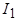 , используя комплексную форму записи величин
, используя комплексную форму записи величин
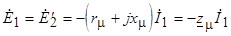 ,
,
где 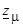 - сопротивление намагничивающего контура;
- сопротивление намагничивающего контура; 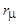 ,
, 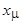 - активная и реактивная составляющие сопротивления намагничивающего контура.
- активная и реактивная составляющие сопротивления намагничивающего контура.
В обмотке статора кроме ЭДС 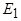 существует еще ЭДС
существует еще ЭДС 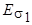 от потока рассеяния
от потока рассеяния 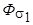 . Действующее значение этой ЭДС представляется комплексом
. Действующее значение этой ЭДС представляется комплексом
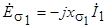 ,
,
где 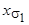 - индуктивное сопротивление рассеяния обмотки статора.
- индуктивное сопротивление рассеяния обмотки статора.
Напряжения, ЭДС и токи фаз обмоток статора и ротора должны удовлетворять уравнениям, которые в комплексной форме записываются аналогично уравнениям трансформатора
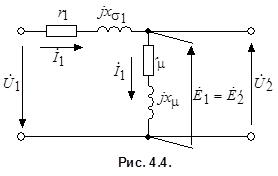
|
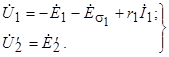 (4.1)
(4.1)
Выражая ЭДС 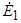 ,
, 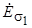 и
и 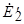 через ток
через ток 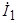 , получим
, получим
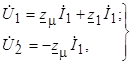 (4.2)
(4.2)
где 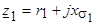 .
.
|
Этим уравнениям соответствует схема замещения асинхронной машины с неподвижной и разомкнутой обмоткой ротора (рис. 4.4). Данная схема аналогична схеме замещения трансформатора на холостом ходу. Отличие состоит лишь в соотношении параметров. Наличие воздушного зазора в машине приводит к существенному снижению реактивной составляющей сопротивления намагничивающего контура 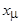 и, следовательно, к увеличению тока намагничивания. В асинхронных машинах ток намагничивания составляет 20-50% от номинального тока, а в трансформаторе он на порядок меньше. По уравнениям (4.1) можно построить также векторную диаграмму, задав напряжение вектора ЭДС
и, следовательно, к увеличению тока намагничивания. В асинхронных машинах ток намагничивания составляет 20-50% от номинального тока, а в трансформаторе он на порядок меньше. По уравнениям (4.1) можно построить также векторную диаграмму, задав напряжение вектора ЭДС 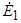 (рис. 4.5). Если совместить эту диаграмму с пространственной диаграммой, то можно получить мгновенные значения фазных напряжений ЭДС и токов, проецируя вращающиеся с угловой скоростью
(рис. 4.5). Если совместить эту диаграмму с пространственной диаграммой, то можно получить мгновенные значения фазных напряжений ЭДС и токов, проецируя вращающиеся с угловой скоростью 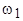 векторы
векторы 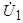 ,
, 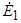 и
и 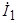 на неподвижные оси АВС.
на неподвижные оси АВС.
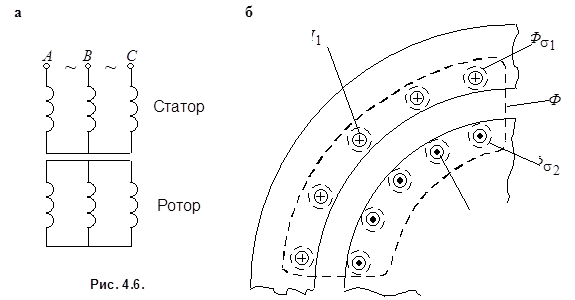
Рассмотрим теперь процессы в асинхронной машине с неподвижным ротором и короткозамкнутой обмоткой ротора (рис. 4.6, а).
При включении обмотки статора на напряжение 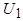 фазные токи
фазные токи 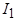 создают основную гармонику МДС
создают основную гармонику МДС 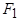 с амплитудой
с амплитудой
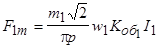 .
.
Токи ротора 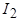 , направленные, в соответствии с правилом Ленца, навстречу токам
, направленные, в соответствии с правилом Ленца, навстречу токам 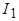 , создадут основную гармонику МДС
, создадут основную гармонику МДС 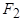 с амплитудой
с амплитудой
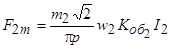 .
.
|
Число фаз обмотки ротора 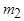 в общем случае не равно числу фаз обмотки статора
в общем случае не равно числу фаз обмотки статора 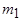 . МДС
. МДС 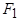 и
и 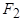 образуют результирующую МДС
образуют результирующую МДС 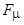 , которая создает основной магнитный поток
, которая создает основной магнитный поток 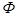 , сцепленный с обеими обмотками.
, сцепленный с обеими обмотками.
Связь между этими МДС в комплексной форме определяется уравнением
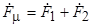 .
.
Выражая МДС через соответствующие токи, получим
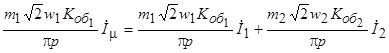 ,
,
где 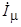 - ток намагничивания, протекающий по обмотке статора.
- ток намагничивания, протекающий по обмотке статора.
Отсюда находим выражение для тока намагничивания 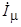 :
:
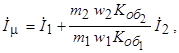
или
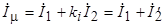 , (4.3)
, (4.3)
где 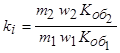 - коэффициент приведения обмотки ротора к обмотке статора по току.
- коэффициент приведения обмотки ротора к обмотке статора по току.
Полученное уравнение называется уравнением токов.
Ток намагничивания 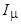 по определению создает в машине основной магнитный поток Ф, который, сцепляясь с обмотками статора и ротора, наводит в них ЭДС
по определению создает в машине основной магнитный поток Ф, который, сцепляясь с обмотками статора и ротора, наводит в них ЭДС
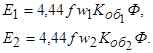
Кроме основного потока в машине существуют также потоки рассеяния 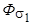 и
и 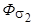 (рис. 4.6, б). Каждый из этих потоков сцепляется только со своей обмоткой и наводит в ней ЭДС рассеяния
(рис. 4.6, б). Каждый из этих потоков сцепляется только со своей обмоткой и наводит в ней ЭДС рассеяния 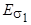 и
и 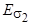 соответственно.
соответственно.
Действующие значения этих ЭДС можно выразить через соответствующие токи в комплексной форме:
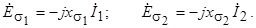
С целью упрощения дальнейшего анализа выполним приведение обмотки ротора к обмотке статора, используя соотношения
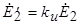 и
и 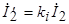 .
.
После приведения получаем
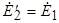 ;
; 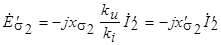 ,
,
где 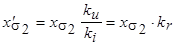 - приведенное значение индуктивного сопротивления рассеяния обмотки ротора;
- приведенное значение индуктивного сопротивления рассеяния обмотки ротора; 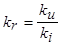 - коэффициент приведения обмотки ротора к обмотке статора по сопротивлению.
- коэффициент приведения обмотки ротора к обмотке статора по сопротивлению.
В соответствии со вторым законом Кирхгофа напряжения, ЭДС и токи обмотки статора и ротора должны удовлетворять уравнениям
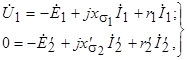 (4.4)
(4.4)
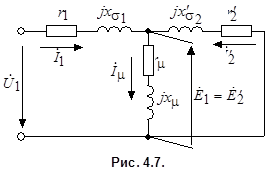
|
где 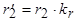 - приведенное значение активного сопротивления обмотки ротора.
- приведенное значение активного сопротивления обмотки ротора.
Уравнения напряжений (4.4) совместно с уравнением тока (4.3) образуют полную систему уравнений асинхронной машины для анализа установившихся режимов.
Уравнения показывают, что асинхронную машину можно заменить Т-образной схемой замещения (рис. 4.7), аналогичной схеме замещения трансформатора в режиме короткого замыкания.
Таким образом, при неподвижном роторе асинхронная машина работает как трансформатор, в котором электрическая энергия статора за вычетом потерь переходит в ротор, где, не совершая никакой полезной работы, превращается в тепло.
4.2. Явления в асинхронной машине при вращающемся роторе.
Замена вращающегося ротора неподвижным
При вращении ротора основной магнитный поток вращается относительно ротора с частотой
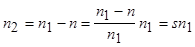 ,
,
пропорциональной скольжению, поэтому частота наведенной в обмотке ротора ЭДС также будет пропорциональна скольжению:
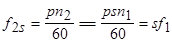 .
.
Действующее значение этой ЭДС определяется выражением
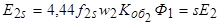 ,
,
где 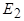 - ЭДС, наведенная в обмотке неподвижного ротора.
- ЭДС, наведенная в обмотке неподвижного ротора.
Индуктивное сопротивление рассеяния обмотки вращающегося ротора также будет пропорционально скольжению:
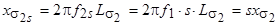 ,
,
где 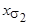 - индуктивное сопротивление рассеяния неподвижного ротора.
- индуктивное сопротивление рассеяния неподвижного ротора.
Зависимость активного сопротивления обмотки ротора от частоты 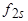 носит более сложный характер (см. п. 4.10). При данном рассмотрении эта зависимость не имеет принципиального значения, поэтому примем
носит более сложный характер (см. п. 4.10). При данном рассмотрении эта зависимость не имеет принципиального значения, поэтому примем 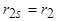 .
.
С учетом сделанных замечаний уравнение напряжений вращающегося ротора будет иметь вид
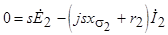 .
.
Отсюда ток ротора
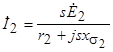 . (4.5)
. (4.5)
Частота этого тока так же, как и частота ЭДС 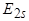 , пропорциональна скольжению. Это обстоятельство существенно затрудняет анализ процессов в асинхронной машине, так как оказывается невозможным совместить электрические цепи статора и ротора. Однако эта проблема может быть снята, если заменить вращающийся ротор неподвижным. Возможность такой замены обусловлена тем, что поле ротора вращается синхронно с полем статора, образуя с ним общее поле машины. Действительно, МДС
, пропорциональна скольжению. Это обстоятельство существенно затрудняет анализ процессов в асинхронной машине, так как оказывается невозможным совместить электрические цепи статора и ротора. Однако эта проблема может быть снята, если заменить вращающийся ротор неподвижным. Возможность такой замены обусловлена тем, что поле ротора вращается синхронно с полем статора, образуя с ним общее поле машины. Действительно, МДС 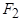 вращается относительно ротора с частотой скольжения
вращается относительно ротора с частотой скольжения 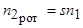 , а сам ротор вращается с частотой
, а сам ротор вращается с частотой 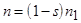 , поэтому частота вращения МДС
, поэтому частота вращения МДС 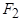 по отношению к статору равна синхронной
по отношению к статору равна синхронной
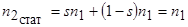 .
.
Таким образом, вращение ротора приводит к изменению частоты ЭДС и тока в обмотке ротора, но не влияет на характер взаимодействия полей статора и ротора. Результат этого взаимодействия останется неизменным, если ротор затормозить, а действующее значение тока ротора 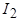 оставить прежним, изменив его частоту с
оставить прежним, изменив его частоту с 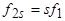 на
на 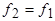 . Для выполнения такой замены достаточно в выражении (4.5) поделить числитель и знаменатель на s:
. Для выполнения такой замены достаточно в выражении (4.5) поделить числитель и знаменатель на s:
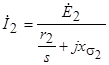 . (4.6)
. (4.6)
Согласно этому выражению ток 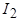 можно рассматривать как ток неподвижного ротора, активное сопротивление которого изменяется обратно пропорционально скольжению s реально вращающегося ротора.
можно рассматривать как ток неподвижного ротора, активное сопротивление которого изменяется обратно пропорционально скольжению s реально вращающегося ротора.
4.3. Уравнения, схема замещения и векторная диаграмма
асинхронной машины
После замены вращающегося ротора неподвижным анализ установившихся процессов в асинхронной машине можно выполнить с помощью полученных ранее уравнений (4.4) и (4.3), если вместо сопротивления 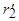 ввести в роторную цепь сопротивление
ввести в роторную цепь сопротивление 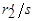 :
:
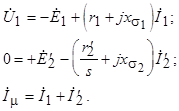
Сопротивление 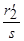 можно представить следующим образом:
можно представить следующим образом:
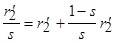 .
.
Тогда уравнения установившегося режима асинхронной машины примут вид
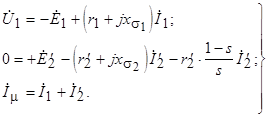 (4.7)
(4.7)
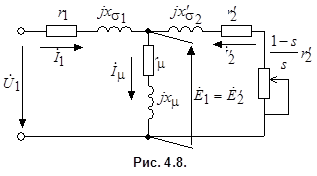
|
Уравнениям (4.7) соответствует Т-образная схема замещения асинхронной машины (рис. 4.8). В этой схеме сопротивление 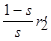 эквивалентно активной нагрузке трансформатора, а в асинхронной машине оно соответствует механической мощности, развиваемой ротором,
эквивалентно активной нагрузке трансформатора, а в асинхронной машине оно соответствует механической мощности, развиваемой ротором,
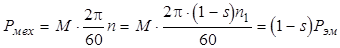 ,
,
где М - электромагнитный момент; 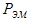 - электромагнитная мощность.
- электромагнитная мощность.
В асинхронной машине с неподвижным ротором электромеханического преобразования энергии не происходит, поэтому вся электромагнитная мощность 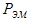 превращается в электрическую мощность, выделяющуюся в виде тепла в сопротивлении
превращается в электрическую мощность, выделяющуюся в виде тепла в сопротивлении 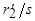 ,
,
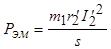 .
.
В реальной вращающейся асинхронной машине в теплоту превращается только часть электромагнитной мощности, определяемая мощностью потерь,
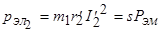 ,
,
а остальная мощность определяет механическую мощность, развиваемую ротором,
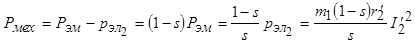 .
.
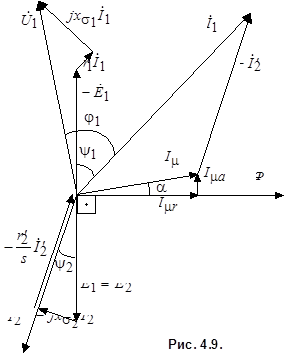
|
Параметры схемы замещения обычно записывают в относительных единицах. Для наиболее распространенных асинхронных двигателей мощностью от 3 до 100 кВт они имеют следующие значения:
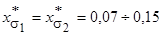 ;
;
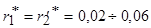 ;
;
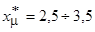 ;
;
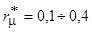 .
.
На основе системы уравнений (4.7) можно построить векторную диаграмму, наглядно иллюстрирующую взаимосвязи в асинхронной машине в рабочих режимах. На рис. 4.9 представлена векторная диаграмма асинхронной машины в режиме двигателя. Она аналогична векторной диаграмме трансформатора, работающего на чисто активную нагрузку. Отличие состоит в относительно большей величине намагничивающего тока 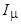 (см. п. 4.2) и в ином физическом толковании вектора Ф. В асинхронной машине - это пространственная функция, распределенная по гармоническому закону и вращающаяся с синхронной частотой, а в трансформаторе поток Ф - это гармоническая функция времени, представленная на комплексной плоскости изображающим вектором
(см. п. 4.2) и в ином физическом толковании вектора Ф. В асинхронной машине - это пространственная функция, распределенная по гармоническому закону и вращающаяся с синхронной частотой, а в трансформаторе поток Ф - это гармоническая функция времени, представленная на комплексной плоскости изображающим вектором 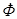 .
.
Дата добавления: 2017-11-21; просмотров: 3580;











