Изображения в сферических зеркалах.
Отражающие поверхности могут иметь не плоскую форму, чаще всего она представляет собой сегмент сферы. Сферическим зеркалом называют поверхность шарового сегмента͵ зеркально отражающую свет. Сферические зеркала бывают выпуклые и вогнутые. Сферическое зеркало принято называть выпуклым, если отражение происходит от внешней стороны поверхности сферического сегмента͵ ᴛ.ᴇ. если центр зеркала находится к источнику света ближе, чем края зеркала. Сферическое зеркало принято называть вогнутым, если отражающей поверхностью служит внутренняя сторона сферического сегмента͵ ᴛ.ᴇ. если центр зеркала находится дальше от источника света.
Для каждого из параллельных лучей, падающих на вогнутое зеркало, в точке их падения выполняются оба закона отражения. В случае если размеры сферического зеркала малы по сравнению с его радиусом кривизны, так что лучи отражаются от него под малым углом, то они пересекутся в точке, которая принято называть фокусом зеркала (точка F на рис.1.3.3). Центром зеркала называют точку А, которая расположена на одинаковом расстоянии от краев зеркала. Расстояние АС представляет собой радиус кривизны зеркала R, а точка 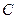 принято называть центром кривизны зеркала. Расстояние между фокусом и центром зеркала AF принято называть фокусным расстоянием зеркала F:
принято называть центром кривизны зеркала. Расстояние между фокусом и центром зеркала AF принято называть фокусным расстоянием зеркала F:
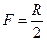 ,
,
где R – радиус кривизны зеркала. На рис. 1.3.3 видно, что фокусное расстояние равно половине радиуса R. Это следует из того, что FA=FB, а треугольник FCB равнобедренный, то есть FC=FB.
Главная ось зеркала определяется как прямая, проходящая через фокус и центр сферического зеркала (на рис. 1.3.3 прямая АС). Луч, направленный вдоль главной оси зеркала, отражаясь, движется по тому же пути в обратном направлении.
Плоскость, проходящую через главный фокус зеркала, расположенный на главной оси, перпендикулярно ей, называют фокальной плоскостью.
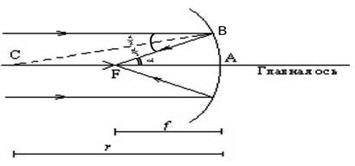
Рис.1.3.3 Вогнутое зеркало.
Формула сферического зеркала. Для вогнутого сферического зеркала радиуса R и предмета͵ расположенного на расстоянии d от центра зеркала, изображение будет располагаться на расстоянии f от центра зеркала,
ĸᴏᴛᴏᴩᴏᴇ определяется по формуле:
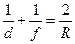 , или:
, или: 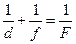
Аналогично для выпуклого зеркала формула отличается только знаком у фокусного расстояния. Это обусловлено тем, что после рассеяния на поверхности выпуклого зеркала лучи будут расходиться. Сходиться будут их продолжения за зеркалом. По этой причине кривизна зеркала считается отрицательной:
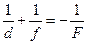
Величину, обратную фокусному расстоянию F сферического зеркала, называют его оптической силой D линзы:
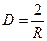
Отношение расстояний от центра зеркала до изображения и до предмета равно отношению размеров изображения Н и предмета h, рассматриваемого в сферическое зеркало:
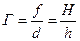
Величина Г принято называть увеличением (уменьшением) зеркала.
На рис.1.3.4 приводятся построения изображений предмета в вогнутом зеркале в случаях, когда предмет располагается ближе и дальше фокусного расстояния (рис.а и рис.б), а также в выпуклом зеркале (рис.в). Правила построения достаточно простые:
- луч, проходящий через фокус зеркала, после отражения становится параллельным и наоборот;
- угол падания луча равен углу его отражения;
- если луч, параллельный главной оси зеркала, падает на выпуклую поверхность, то через главный фокус зеркала проходит продолжение луча;
- луч, проходящий через центр сферической поверхности, после отражения от зеркала возвращается по тому же пути (в связи с этим рассматриваемая точка 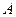 , центр кривизны зеркала
, центр кривизны зеркала 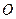 , и изображение точки
, и изображение точки 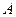 - точка
- точка 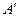 лежат на одной линии).
лежат на одной линии).
На рис.1.3.4а изображение представляет собой пересечение двух лучей. Первый идет параллельно главной оптической оси, и после отражения от зеркала проходит через его главный фокус 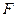 . Второй луч из точки
. Второй луч из точки 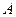 проходит через фокус зеркала
проходит через фокус зеркала 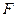 , и, отражаясь от зеркала, идет параллельно главной оптической оси. Точка
, и, отражаясь от зеркала, идет параллельно главной оптической оси. Точка 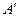 представляет собой пересечение двух описанных лучей. Точку пересечения можно получить, направив луч в центр зеркала
представляет собой пересечение двух описанных лучей. Точку пересечения можно получить, направив луч в центр зеркала 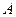 , и построив угол отраженного луча, равный углу падающего луча. При этом такой способ используется при построении изображений редко, так как достаточно первых двух лучей.
, и построив угол отраженного луча, равный углу падающего луча. При этом такой способ используется при построении изображений редко, так как достаточно первых двух лучей.
На рис.1.3.4б, когда источник света располагается ближе к зеркалу, чем его фокус 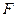 Первый луч их точки А соединяется с центром кривизны зеркала О. По правилам построения изображений он должен пройти через точку
Первый луч их точки А соединяется с центром кривизны зеркала О. По правилам построения изображений он должен пройти через точку 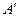 . Второй луч движется параллельно главной оси зеркала. Он проходит через фокус зеркала, его продолжение через точку
. Второй луч движется параллельно главной оси зеркала. Он проходит через фокус зеркала, его продолжение через точку 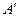 . Положение конца вектора – точки
. Положение конца вектора – точки 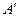 получается пересечением этих двух лучей. Похожим образом можно построить изображение в третьем случае. Луч из точки
получается пересечением этих двух лучей. Похожим образом можно построить изображение в третьем случае. Луч из точки 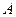 проводится параллельно главной оптической оси. Точка пересечения с поверхностью зеркала соединяется с главным фокусом. Вторая линия соединяет точку
проводится параллельно главной оптической оси. Точка пересечения с поверхностью зеркала соединяется с главным фокусом. Вторая линия соединяет точку 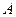 с центром кривизны зеркала
с центром кривизны зеркала 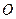 . Пересечение первой и второй линии происходит в точке
. Пересечение первой и второй линии происходит в точке 
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, вогнутое зеркало на практике действует как увеличительное стекло. Их применяют, как линзы в телескопах, биноклях. Хорошо известно, что таким зеркалом пользуются при осмотре больных отоларингологи, офтальмологи. Хорошо известно, что если лампочка карманного фонарика оказывается в фокусе зеркала отражателя, то луч света практически не расширяется с расстоянием, и мы можем осветить далекие предметы. Так работают и фары автомобиля, и прожектор.
Для того, чтобы изображение было четким, лучи должны сходиться в одной точке. Сферическое зеркало не создает такого четкого изображения, как и плоское зеркало, так как свет разной длины волны отражается от зеркала под различными углами.
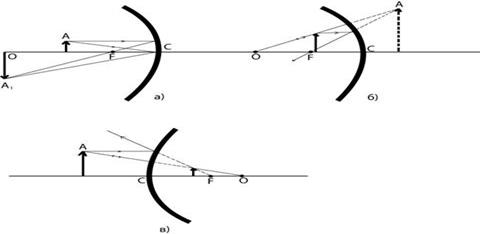
Рис. 1.3.4. Построение изображения предмета в вогнутом (а) и (б) и выпуклом (в) зеркалах.
Особенности изображений в зеркалах
| зеркало | Расположение предмета | Расположение изображения | Особенности изображения |
| плоское | любое | За зеркалом, на том же расстоянии, что и предмет | Мнимое, прямое, обращенное, по величине равно самому предмету |
| Выпуклое сферическое | любое | Между главным фокусом и зеркалом | Мнимое, прямое, уменьшенное |
| Вогнутое сферическое | В бесконечности | В главном фокусе | Действительное, перевернутое, уменьшенное |
| За оптическим центром на конечном расстоянии | Между главным фокусом и оптическим центром | Действительное, перевернутое, уменьшенное | |
| В оптическом центре | В оптическом центре | Действительное, перевернутое, по величине равно самому предмету | |
| Между оптическим центром и главным фокусом и | За оптическим центром | Действительное, перевернутое, уменьшенное | |
| Между главным фокусом и зеркалом | За зеркалом | Мнимое, прямое, увеличенное |
Контрольные вопросы
1. Где находится изображение точечного источника, даваемое плоским зеркалом? Ответ обосновать геометрическими построениями.
2. Что называется сферическим зеркалом? Что такое оптический центр, полюс, главная и побочная оптические оси зеркала?
3. Формула сферического зеркала. Дать определения главного и побочного фокусов, фокальной плоскости, оптической силы зеркала.
4. Показать, что изображение зеркалом перпендикулярного главной оптической оси отрезка является также перпендикулярным этой оси отрезком
5. Изобразить гомоцентрические пучки, соответствующие: а) действительному и мнимому изображениям; б) действительному и мнимому источникам.
6.Сформулировать правило знаков для формулы сферического зеркала.
7. Формула линейного увеличения зеркала.
8. Почему в тонкостенном стакане с водой ложечка кажется увеличенной?
(Ответ: вода в стакане выполняет роль цилиндрической собирающей линзы. Мы видим мнимое увеличенное изображение)
9. Каким образом в ясную погоду можно определить фокусное расстояние собирающей линзы? (Решение. Расстояние от Солнца до Земли столь велико, что все лучи, падающие на линзу, параллельны друг другу. Если на экране получить изображение Солнца, то расстояние от линзы до экрана будет равно фокусному расстоянию)
Дата добавления: 2017-11-21; просмотров: 5038;











