Корреляционный интеграл

На практике часто встречается ситуация, которая характеризуется следующим признаками:

1. Сообщения 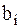, i=1, 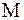на выходе источника появляются равновероятно;

2. Соответствующие этим сообщениям сигналы 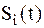полностью известны на приемной стороне, так как полагаем, что эти сигналы передаются по каналу с постоянными параметрами (т.е. коэффициент передачи m и время задержки в канале 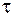известны).

Метод приема сигналов с полностью известными параметрами называется когерентными, а устройство, его реализующее - когерентным приемником. Особенность этого приемника: в нем необходимо знать точное значение фазы приходящих сигналов. Задача эта чрезвычайно сложная и далеко не всегда ее удается решить.

Решим задачу синтеза оптимального когерентного приемника в условиях аддитивного белого шума. Колебания на входе РПУ запишем соотношением:

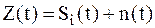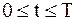
;		(1.1)
где		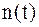–	аддитивный БГШ с нулевым средним значением и спектральной плотностью мощности (СПМ)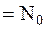

Так как в выражении (1.1) читается случайным только белый шум, то он и является источником ошибок.

Получателю не известен так же вариант переданного сигнала (индекс ).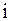

Для решения этой задачи применим правило максимального правдоподобия.

Решение:

Считаем, что сигналы 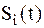является финитными с длительностью 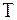. Полагаем, что известны границы тактового интервала, на котором происходит обработка принимаемого колебания, т. е. в системе обеспечена надежная тактовая синхронизация.

В целях упрощения решаемой задачи помеху, являющуюся белым шумом, заменим на квазибелый шум. Данный СП имеет СПМ 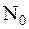в полосе частот 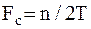. Аналоговые сигналы 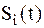представим в дискретном виде, воспользовавшись теоремой Котельникова.

Тогда в канал связи будет поступать выбранный из некоторого множества вектор:

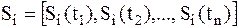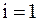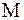
; ,	(1.2)
где		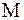–	число сигналов (сообщений)
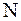
	–	число отсчетов сигнала в течение длительности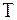

;

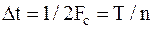(1.3)

При передаче вектор 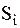искажается помехой и на вход приемника поступает аддитивная смесь:

;

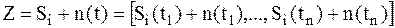(1.4)

Для принятия решения о передаче символа 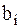, , 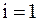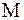в приемнике максимизируется величина: .

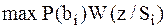Далее вероятности 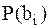, не учитываются ввиду равновероятной передачи сообщений.

Рассмотрим .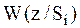

;

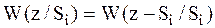(1.5)

так как 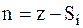, т.е. отличие принятого колебания от переданного определяется только случайным процессом, которым является шум.

Так как сигнал и помеха в канале статически не зависимы,

;

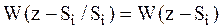(1.6)

Иными словами: появление на выходе РпдУ любого из 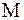равновероятных векторов сигнала не оказывает влияние на плотность распределения аддивного гауссовского шума, которая определяется соотношением:

;

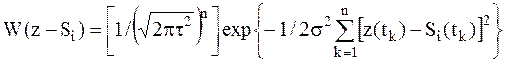(1.7)

В этом выражении первый сомножитель от индекса 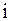не зависит и на решение, выносимое приемником не влияет. Поэтому далее он не учитывается.

Заменим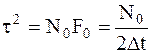

Это выражение следует из того, что при переходе от аналоговых сигналов к векторам путем дискретизации по Котельникову аналогичной операции подвергается и белый шум, который был представлен как квазибелый.

Поэтому после подстановки и логарифмирования получаем:

;

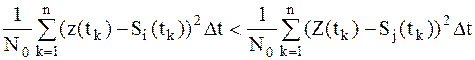(1.8)

Ясно, что максимальная (потенциальная) помехоустойчивость оптимального приемника будет реализована при обработке сигнала в течение всей посылки длительности 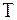, а не в дискретных отсчетах.

Поэтому вновь вернемся к задаче для БШ. Для этого будем расширять полосу 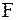, тогда число отсчетов 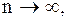a

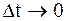
Суммы превратятся в интегралы, а процедура обработки имеет вид:

;

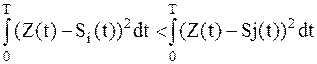(1.9)

После возведения в квадрат и упрощения имеем:

;

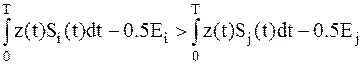(1.10)

Для двоичной системы, где энергии равны, имеем:

;

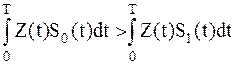(1.11)

Из соотношения (1.10) и (1.11) видно, что процедура обработки сигналов в оптимальном РПУ не содержит никаких вероятностей.

;

–

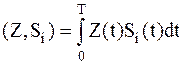данное скалярное произведение носит название корреляционного интеграла

(1.12)

Поэтому устройство реализующее данную операцию называется корреляторомили активным фильтром. Рассмотрим оптимальный по Котельникову приемник, реализованный с использованием корреляторов (активных фильтров).