Два распределения, связанные с нормальным законом
Сформируем два результата, которые понадобятся далее.
 Теорема 1.Пусть случайные величины
Теорема 1.Пусть случайные величины 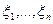 независимы и нормальны с параметрами (0, 1), тогда случайная величина
независимы и нормальны с параметрами (0, 1), тогда случайная величина 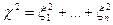 подчинена закону распределения с плотностью вероятности
подчинена закону распределения с плотностью вероятности
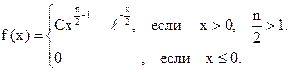
Где число n называется числом степеней свободы.

Рис. 1. 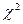 – распределение (Пирсона).
– распределение (Пирсона).
Теорема 2. Пусть случайные величины 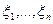 независимы и нормальны с параметрами (0, 1), тогда случайная величина
независимы и нормальны с параметрами (0, 1), тогда случайная величина 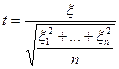 подчинена закону распределения с плотностью вероятности:
подчинена закону распределения с плотностью вероятности:
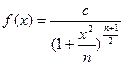
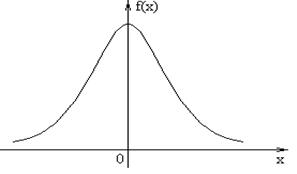
Рис. 2.t – распределение (Стьюдента).
В обоих случаях константа С подобрана так, чтобы площадь под графиком плотности была равна 1.
Квантиль распределения.Пусть имеется случайная величина 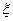 с функцией распределения F(x). Будем предполагать, что функция F(x) непрерывна и строго монотонна.
с функцией распределения F(x). Будем предполагать, что функция F(x) непрерывна и строго монотонна.
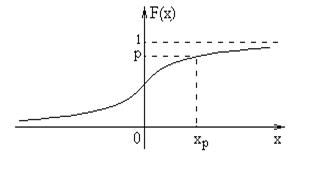
Рис. 3
Зададим число pÎ (0, 1).
Квантилем уровня p распределения F(x)называется корень уравнения F(x) = p, х - ?
Обозначим его 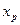 (см. рис. 3). Из определения функции F(x) вытекает:
(см. рис. 3). Из определения функции F(x) вытекает: 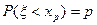 .
.
Нам понадобится далее квантили распределений Пирсона и Стьюдента. Они обозначаются: 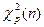 ,
, 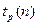
Для этих квантилей имеются таблицы.
Дата добавления: 2019-12-09; просмотров: 783;











