Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации
Для выполнения инженерных расчетов, связанных с прогнозированием по массовым случайным явлениям и основанных на методах теории вероятностей, необходимо знать параметры случайных величин, участвующих в этих расчетах: математическое ожидание, дисперсию и т.д.
1. Оценка 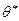 называется состоятельной,если при неограниченном увеличении объема выборки
называется состоятельной,если при неограниченном увеличении объема выборки 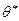 сходится по вероятности к истинному значению параметра
сходится по вероятности к истинному значению параметра 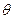 :
:
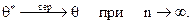
Это означает: при достаточно большом объеме выборки с практической достоверностью (с вероятностью, близкой к единице) 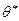 практически совпадает с истинным значением
практически совпадает с истинным значением 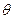 .
.
2. Оценка 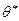 называется несмещенной, если ее математическое ожидание совпадает с истинным значением параметра
называется несмещенной, если ее математическое ожидание совпадает с истинным значением параметра 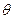 :
: 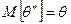 .
.
3. Оценка 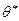 называется эффективной, если она несмещенная и при этом имеет наименьшую дисперсию (наименьший разброс относительно
называется эффективной, если она несмещенная и при этом имеет наименьшую дисперсию (наименьший разброс относительно 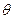 ) по сравнению с другими несмещенными оценками параметра
) по сравнению с другими несмещенными оценками параметра 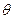 .
.
Пусть с испытанием связана случайная величина 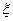 с неизвестными числовыми характеристиками (а, D) и пусть набрана независимая выборка
с неизвестными числовыми характеристиками (а, D) и пусть набрана независимая выборка 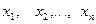 .
.
В дальнейшем будем употреблять следующий удобный термин: любую функцию 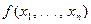 от выборки
от выборки 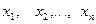 будем называть статистикой.
будем называть статистикой.
Лемма 1. Статистика

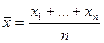
является состоятельной несмещенной оценкой математического ожидания а.
Доказательство
1. Мы знаем, что элементы выборки 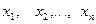 являются независимыми случайными величинами с одним и тем же законом распределения, совпадающим с законом распределения случайной величины
являются независимыми случайными величинами с одним и тем же законом распределения, совпадающим с законом распределения случайной величины 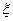 , а значит, имеют те же числовые характеристики (а, D).
, а значит, имеют те же числовые характеристики (а, D).
По теореме Чебышева среднее арифметическое независимых случайных величин с одинаковыми параметрами (а, D), при неограниченном возрастании числа слагаемых сходится по вероятности к общему математическому ожиданию
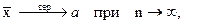
что и означает состоятельность оценки.
2. Имеем
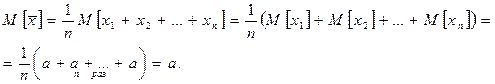
Это означает несмещенность оценки 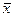 .
.
 Лемма 2.Статистика
Лемма 2.Статистика
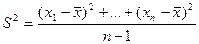
является состоятельной несмещенной оценкой дисперсии D. (Доказывается аналогично лемме 1).
Замечание 1. Если в формуле заменить (n - 1) на n , то оценка останется состоятельной, но будет смещенной. Величина S2 называется исправленной дисперсией.
Замечание 2.Из леммы 2 следует, что статистика:

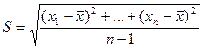
является состоятельной оценкой для СКО 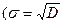 ). Можно доказать, что
). Можно доказать, что 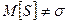 , т.е. оценка S является смещенной оценкой для
, т.е. оценка S является смещенной оценкой для 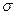 .
.
Пусть по данным опыта получим ряд значений случайной точки ( 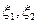 ) (выборка):
) (выборка):
(х1, у1) (х2, у2), …, (хn, уn).
Справедлива следующая
Лемма 3.Состоятельной несмещенной оценкой для cov( 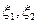 ) является выборочная ковариация
) является выборочная ковариация
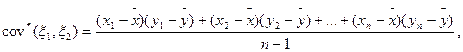
где 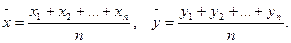
Дата добавления: 2019-12-09; просмотров: 1090;











