Расчет сварной главной балки балочной клетки
Сечение главной балки принимаем двутавровое симметричное составное из листовой стали С 285 с Ry = 260 Мпа = 26 кН/см2.
Нормативная равномерно распределенная нагрузка на главную балку включает нагрузку от вышележащих конструкций, собственный вес главной балки и временную нагрузку на перекрытие
qn = (gn + pn)·В, где gn – постоянная нагрузка от веса перекрытия;
gn = gnнаст. + gnб.н. + gnгл.б.,
gnнаст. + gnб.н. = 1,385 кН/м2;
gnгл.б. = 0,02·(gnнаст. + gnб.н. + pn), gnгл.б. = 0,02·(1,385 + 24) = 0,51 кН/м2;
gn = 1,385 + 0,51 = 1,895 кН/м2; qn = (1,895 + 24)·7,7 = 199,39 кН/м2.
Расчетная равномерно распределенная нагрузка на главную балку равна 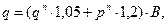 q = (1,895·1,05 + 24·1,2)·7,7 = 237,08 кН/м.
q = (1,895·1,05 + 24·1,2)·7,7 = 237,08 кН/м.
Расчетный изгибающий момент в середине пролета главной балки равен:  ,
, 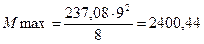 кН*м.
кН*м.
Расчетная поперечная сила на опоре
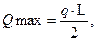
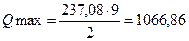 кН.
кН.
В целях экономии металла проектируем балку переменного по длине сечения, а поэтому развитие пластических деформаций допускаем только в сечении с максимальным изгибающим моментом:
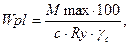
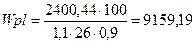 см3,
см3,
где с = 1,1 – коэффициент, учитывающий пластическую работу металла;
γc = 0,9 – коэффициент, учитывающий условия работы сварных металлических конструкций, величина которого приведена в табл. 1 СП 16.13330.2011 «Стальные конструкции» или в табл. Б.4 прил. Б.
Назначаем высоту сечения главной балки из условия экономии стали, максимально допустимого прогиба и строительной высоты перекрытия.
Оптимальная высота балки из условия экономии стали определяется по формуле 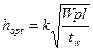 ,
,
где 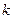 – коэффициент, учитывающий конструктивное решение балки,
– коэффициент, учитывающий конструктивное решение балки, 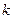 = 1,15 – для сварных балок;
= 1,15 – для сварных балок;
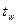 – толщина стенки балки, определяется по эмпирической формуле:
– толщина стенки балки, определяется по эмпирической формуле: 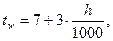 где
где 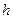 - ориентировочная высота главной балки.
- ориентировочная высота главной балки.
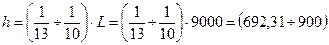 мм.
мм.
Предварительно принимаем h = 900 мм кратно 50 мм.
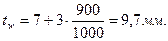 Предварительно принимаем tw = 10 мм.
Предварительно принимаем tw = 10 мм.
 см.
см.
Минимальная высота балки из условия жесткости определяется по формуле: 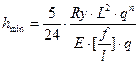 ,
,
где  - предельно допустимый прогиб конструкции, величина которого определяется в соответствии с требованиями главы 15 и прил. Е СП 20.13330.2012 «Нагрузки и воздействия» или по табл. Б.5 прил. Б.
- предельно допустимый прогиб конструкции, величина которого определяется в соответствии с требованиями главы 15 и прил. Е СП 20.13330.2012 «Нагрузки и воздействия» или по табл. Б.5 прил. Б. 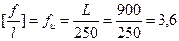 см.
см.
E = 2,06·104 кН/см2;
 см.
см.
Возможная высота главной балки с учетом заданной строительной высоты перекрытия при поэтажном опирании балок вычисляется
hвозм. = hстр. – tнаст. – hб.н., hстр. = 1,6 м = 160 см;
tнаст. = 10 мм = 1 см;
hвозм. = 160 – 1 – 40 = 119 см.
Для дальнейшего расчета принимаем высоту главной балки hw = 110 см.
Толщина стенки определяется из соответствия двум условиям: прочности стенки на срез и местной устойчивости стенки.
1. Требуемая толщина из условий прочности стенки на срез:
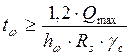 , где Rs – расчетное сопротивление материала стенки срезу;
, где Rs – расчетное сопротивление материала стенки срезу;
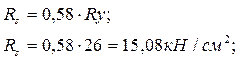
γс = 0,9;
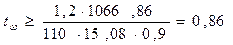 см;
см;
1 см > 0,86 см – условие выполняется, конструктивно принимаем tw = 1,2 см.
2. Для обеспечения местной устойчивости стенки без укрепления продольным ребром жесткости в балках высотой до 2 м должно соблюдаться соотношение 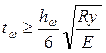 , где hw – высота стенки;
, где hw – высота стенки; 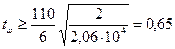 см;
см;
1,2 см > 0,65 см – условие выполняется, толщина стенки достаточна. Окончательно принимаем tw = 1,2 см.
Требуемая площадь сечения пояса: 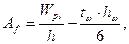
где Wpl – требуемый момент сопротивления; h – высота балки;
tw – толщина стенки;
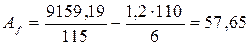 см2.
см2.
При назначении размеров поясов выполняем следующие условия. Во избежание усадочных напряжений при сварке выдерживаем соотношение 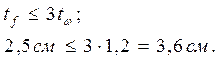
Минимальную ширину поясного листа задаем, исходя из требований общей устойчивости балки: 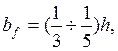
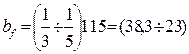 см.
см. 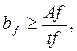

По технологическим соображениям (для удобства автоматической сварки) ширина поясного листа должна быть не менее 180 мм. Принимаем в соответствии с сортаментом стали bf = 26 см.
Подобранное сечение балки проверяем на прочность. По назначенным размерам балки вычисляем фактические геометрические характеристики поперечного сечения. Момент инерции сечения
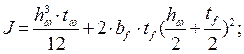
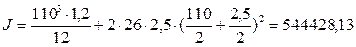 см4.
см4.
Статический момент площади половины сечения
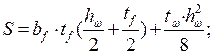
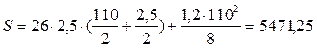 см3.
см3.
Момент сопротивления сечения равен 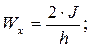
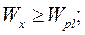
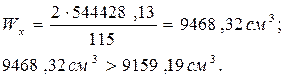
Далее устанавливаются значения наибольших нормальных напряжений в балке 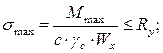
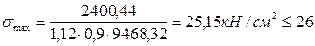 кН/см2 – условие выполняется.
кН/см2 – условие выполняется.
Δσ=(Ry-σmax)*100% Ry=(26-25,15)*100%/26=3,26%<5%.
При этом наибольшие касательные напряжения в балке:
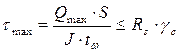 ,
,
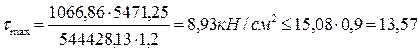 кН/см2.
кН/см2.
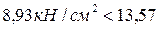 кН/см2, условие выполняется.
кН/см2, условие выполняется.
К верхнему поясу балки приложена сосредоточенная нагрузка, дополнительно проверяется стенка на местное давление:
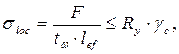
где σloc – местное напряжение смятия;
F – расчетная сосредоточенная нагрузка;
F = (g + p)·l·B, g = gn·1,05; p = pn·1,2;
lef – условная длина распределения статической нагрузки на балке;
lef = b + 2·tf, b – длина нагруженного участка пояса (ширина полки поперечной балки); tf – толщина пояса;
b = 155 мм = 15,5 см – для двутавра № 40; lef = 15,5 + 2·2,5 = 20,5 см;
g = 1,385·1,05 = 1,45 кН/м2; p = 24·1,2 = 28,8 кН/м2;
F = (1,45 + 28,8)·0,95·7,7 = 221,28 кН;
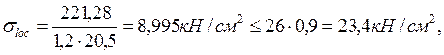
8,995 кН/см2 < 23,4 кН/см2 – условие выполняется.
Определяется относительный прогиб балки с помощью следующей формулы:
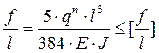 , где
, где 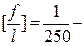 предельно относительный прогиб изгибаемых элементов металлических конструкций в соответствии с требованиями главы 15 и прил. Е СП 20.13330.2012 «Нагрузки и воздействия» или по табл. Б.5 прил. Б;
предельно относительный прогиб изгибаемых элементов металлических конструкций в соответствии с требованиями главы 15 и прил. Е СП 20.13330.2012 «Нагрузки и воздействия» или по табл. Б.5 прил. Б;
qn = 199,39 кН/м = 1,9939 кН/cм;
l = L = 9 м = 900 см;
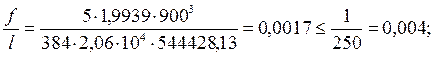
0,0017 < 0,004 – условие выполняется, жесткость достаточна.
Место изменения сечения поясов балки принимаем на расстоянии х от опоры:
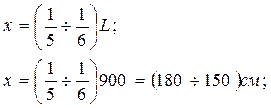
Принимаем х = 165 см = 1,65 м.
Находим расчетный момент в сечении: 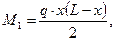
q = 237,08 кН/см2; L = 9 м;
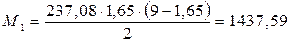 кН*м.
кН*м.
Требуемый момент сопротивления сечения балки при выполнении стыка полуавтоматической сваркой:
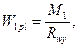 где
где  – расчетное сопротивление сварного соединения на растяжение и изгиб, равное
– расчетное сопротивление сварного соединения на растяжение и изгиб, равное 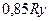 = 0,85·26 = 22,1 кН/см2 ;
= 0,85·26 = 22,1 кН/см2 ;
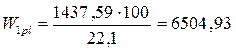 см3.
см3.
Требуемый момент инерции измененного сечения 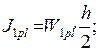
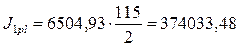 см4.
см4.
Момент инерции, приходящийся на поясные листы 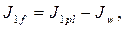
где 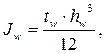
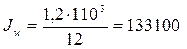 см4;
см4;
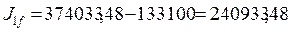 см4.
см4.
Требуемая площадь поясных листов 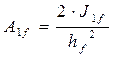 ,
,
где hf – расстояние между центрами тяжести поясов; 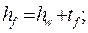
hf = 110 + 2,5 = 112,5 см; 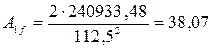 см2.
см2.
Ширину поясных листов  назначаем исходя из следующих условий:
назначаем исходя из следующих условий:
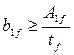 , т.е.
, т.е. 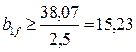 см;
см; 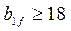 см и
см и 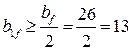 см
см
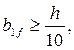 т.е.
т.е. 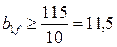 см.
см.
Принимаем b1f’ = 18 см.
Момент инерции измененного сечения балки
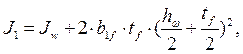
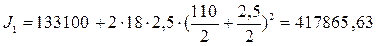 см4.
см4.
Момент сопротивления измененного сечения
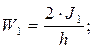
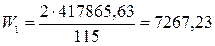 см3.
см3.
С помощью соответствующих вычислений проверяются нормальные напряжения: 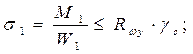
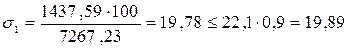 кН/см2.
кН/см2.
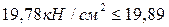 кН/см2 – условие выполняется.
кН/см2 – условие выполняется.
Проверяем наибольшие касательные напряжения по нейтральной оси сечения, расположенного у опоры балки:
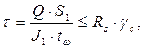 где
где 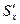 – статический момент балки измененного сечения:
– статический момент балки измененного сечения: 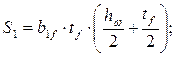
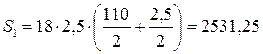 см3;
см3;
Rs = 0,58·26 = 15,08 кН/см2;
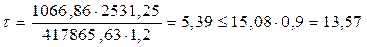 кН/см2.
кН/см2.
5,39 кН/см2 < 13,57 кН/см2 – условие выполняется.
Производится проверка на совместное действие нормальных и касательных напряжений на уровне поясного шва в уменьшенном сечении балки. Поскольку опирание балок настила на главную поэтажное, 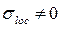 , то приведенные напряжения рассчитываются по формуле
, то приведенные напряжения рассчитываются по формуле 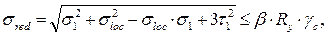
где β – коэффициент, учитывающий развитие в стенке пластических деформаций; β = 1,15;
σloc – местное напряжение смятия; 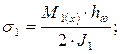
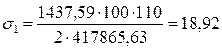 кН/см2.
кН/см2.
 где
где 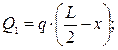
 кН;
кН;
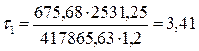 кН/см2.
кН/см2.
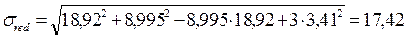 кН/см2
кН/см2
17,42 кН/см2 < 1,15*26*0,9=26,91 кН/см2 – условие выполняется.
Балка под действием нагрузки в плоскости наибольшей жесткости может потерять свою первоначальную форму равновесия, что выражается в боковом выпучивании сжатого пояса и закручивании балки в целом. Это явление называется потерей общей устойчивости балки.
Выпучивание происходит на участках между точками закрепления сжатого пояса. Соответствующие расстояния характеризуют свободную (расчетную) длину балки lef. Общая устойчивость тем выше, чем меньше отношение свободной длины к ширине сжатого пояса lef / bf и чем больше отношение моментов инерции Ix / Iy.
Если отношение lef / bf не превышает значений, вычисленных при  и
и 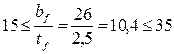 по формуле
по формуле
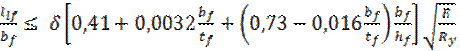 ;
;
при упругой работе сечения δ=1
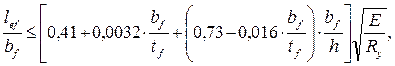
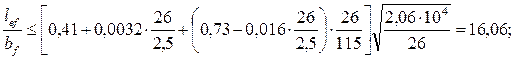
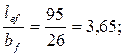 3,65 < 16,06 – условие выполняется, общую устойчивость балки можно считать обеспеченной.
3,65 < 16,06 – условие выполняется, общую устойчивость балки можно считать обеспеченной.
В месте измененного сечения балки проверяется аналогичное требование для уменьшенной ширины сечения
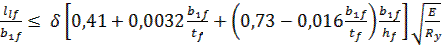 ;
;
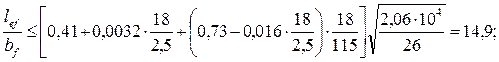
где b1f =18 см, ширина сечения пояса в месте изменения сечения, см.
3,65 < 14,9 – условие выполняется, общую устойчивость балки можно считать обеспеченной.
Местная устойчивость сжатого поясного листа считается обеспеченной, если соблюдается условие: 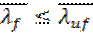 , где
, где 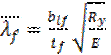 ;
;
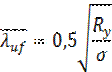
σ=Ry; в упругой стадии работы материала: 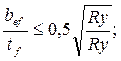
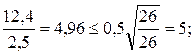 4,96 < 5 – условие выполняется.
4,96 < 5 – условие выполняется.
При развитии пластических деформаций: 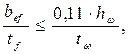
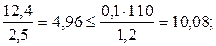 но не более
но не более 
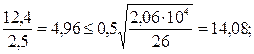 4,96 < 10,08;
4,96 < 10,08;
4,96 < 14,08 – условия выполняются.
Местная устойчивость стенок балки обеспечена, если условная гибкость стенки 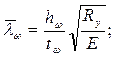
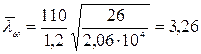 ,
,
не превышает значений 2,5 – при наличии местных напряжений в балках с двусторонними поясными швами.
В случае 3,26 > 2,5 стенки балки укрепляем поперечными ребрами жесткости. Расстояние между основными поперечными ребрами не должно превышать a1 = 2·h при 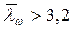 .
.
Принимаем a1 = 2·110 = 220 см = 2200 мм.
Ширина ребра жесткости: 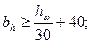
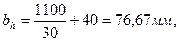 принимаем bh = 80 мм.
принимаем bh = 80 мм.
Толщина ребра 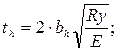
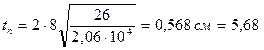 мм, принимаем th = 6 мм.
мм, принимаем th = 6 мм.
При наличии местного напряжения ( 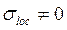 ) местную устойчивость стенки проверяем по формуле, приведенной ниже:
) местную устойчивость стенки проверяем по формуле, приведенной ниже:
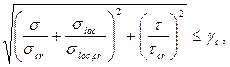 где σ – краевое сжимающее напряжение у расчетной границы отсека, равное 25,15 кН/см2 ; σloc – местные напряжения смятия;
где σ – краевое сжимающее напряжение у расчетной границы отсека, равное 25,15 кН/см2 ; σloc – местные напряжения смятия; 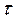 – касательное напряжение, вычисленное по среднему значению поперечной силы.
– касательное напряжение, вычисленное по среднему значению поперечной силы.
При  и поэтажном опирании балок проверку устойчивости выполняют дважды (по теории расчетов – случаи Б и В).
и поэтажном опирании балок проверку устойчивости выполняют дважды (по теории расчетов – случаи Б и В).
Случай Б: 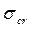 – критические нормальные напряжения определяется по формуле
– критические нормальные напряжения определяется по формуле 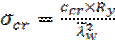 ; при а1/ hw=0,67,
; при а1/ hw=0,67,
где ccr – коэффициент для сварных балок, принимаемый по табл. 12 СП 16.13330.2011 «Стальные конструкции» или по табл. Б.8 прил. Б пособия в зависимости от коэффициента δ;
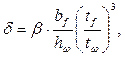 где
где 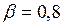 для сварных балок;
для сварных балок;
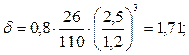 по интерполяции ccr=32,76.
по интерполяции ccr=32,76. 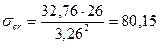 кН/см2.
кН/см2.
σloc,cr определяется по формуле 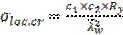 ,
,
где с1 – коэффициент, устанавливаемый в соответствии с данными табл. 14 СП 16.13330.2011 «Стальные конструкции» или по табл. Б.9 прил. Б пособия в зависимости от отношения сторон проверяемой пластины a2/hw,при а2/ hw=0,67 и относительной длины загружения пластины местной нагрузкой ρ, hw=110 см; a2/hw=0,67.
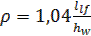 ; llf = 20,5 см; ρ=1,04*20,5/110=0,194, тогда по интерполяции с1=23,59;
; llf = 20,5 см; ρ=1,04*20,5/110=0,194, тогда по интерполяции с1=23,59;
с2 – коэффициент, значение которого принимается по табл. 15 СП 16.13330.2011 «Стальные конструкции» или по табл. Б.10 прил. Б пособия в зависимости от отношения сторон проверяемой пластины a2/hw =0,67 и δ=1,71–степени упругого защемления стенки в поясах, с2=1,617;
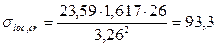 кН/см2.
кН/см2.
Действующие касательные напряжения равны 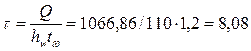 кН/см2.
кН/см2.
Критические касательные напряжения 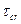 находим по нижеприведенной формуле:
находим по нижеприведенной формуле: 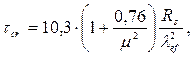
где 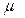 – отношение большей стороны пластинки к меньшей, равное
– отношение большей стороны пластинки к меньшей, равное 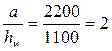 ;
; 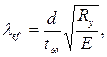
где d – меньшая из сторон пластинки, равная 110 см;
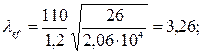 Rs = 0,58*Ry = 0,58*26 = 15,08 кН/см2;
Rs = 0,58*Ry = 0,58*26 = 15,08 кН/см2;
σ = 25,15 кН/см2;
σloc = 8,995 кН/см2;
τ = 8,08 кН/см2;
γc = 0,9;
 кН/см2;
кН/см2;
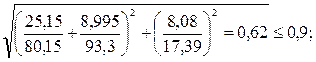
0,62 < 0,9 – условие выполняется.
Случай В: при а1/ hw=2 определяем по интерполяции ccr=84,7 по табл. Б.11 прил. Б пособия. 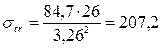 кН/см2.
кН/см2.
σloc,cr определяем по формуле 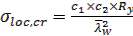
При а1/ hw=2 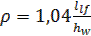 ; llf = 20,5 см; ρ=1,04*20,5/110=0,194,
; llf = 20,5 см; ρ=1,04*20,5/110=0,194,
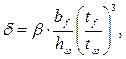 где
где 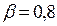 – для сварных балок;
– для сварных балок; 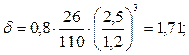 тогда по интерполяции с1=15,36 по табл. Б.9 прил. Б пособия; с2=1,766 по табл. Б.10 прил. Б пособия.
тогда по интерполяции с1=15,36 по табл. Б.9 прил. Б пособия; с2=1,766 по табл. Б.10 прил. Б пособия.
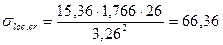 кН/см2.
кН/см2.
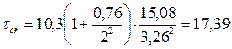 кН/см2.
кН/см2.
 .
.
Проведенные проверки показали, что запроектированная балка удовлетворяет требованиям прочности, прогиба, общей и местной устойчивости.
При поперечном изгибе пояса составной балки стремятся сдвинуться относительно стенки. Сила сдвига возникает за счет разности нормальных напряжений в смежных сечениях пояса. Ее воспринимают непрерывные угловые сварные швы. Швы выполняем двухсторонние, автоматической сваркой в лодочку, сварочной проволокой Св-08А. Для сварочной проволоки Св-08А по табл. Б.14 прил. Б пособия имеем Rwf=18 кН/см2. По табл. 7 прил. Б пособия для стали С 285 с Run = 380 Мпа = 38 кН/см2 определяем Rwz=0,45 Run=17,1 кН/см2.
При толщине свариваемых деталей 25 мм минимальный катет шва равен 7 мм по табл. Б.12 прил. Б пособия, при этом для автоматической сварки по табл. 13 прил. Б пособия коэффициенты проплавления равны βf=1,1 и βz=1,15. Тогда βf* Rwf=1,1*18=19,8 кН/см2; βz* Rwz=1,15*17,1=19,67 кН/см2; отсюда выбираем минимальное значение 19,67 кН/см2.
Требуемая толщина швов в двухстороннем шве  ,
,
где Q1 – поперечная сила в месте изменения сечения, равная 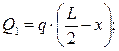
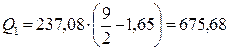 кН;
кН;
S1 – статический момент площади сечения пояса относительно нейтральной оси, равный
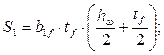
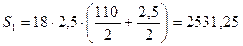 см3.
см3.
Rw = 19,67 кН/см2 – расчетное минимальное сопротивление металла шва сварных соединений с угловыми швами.
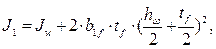
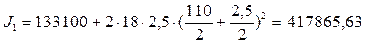 см4.
см4.
γw = 1 – коэффициент условия работы сварочного соединения;
γс = 0,9;
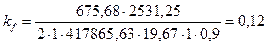 см=1,2 мм.
см=1,2 мм.
Принимается kf = 7 мм, т.к. это минимальное значение kf при автоматической сварке. Во избежание больших усадочных напряжений поясные швы устраиваем сплошными, одинаковой толщины, используя автоматическую сварку.
Расчет опорной части балки сводится к определению толщины опорного ребра.
В связи с тем, что опирание сварных балок на нижележащие конструкции является шарнирным, передача опорной реакции осуществляется через парные опорные ребра, плотно пригнанные или приваренные к нижнему поясу балки.
Размеры опорного ребра устанавливаем из расчета на смятие его торцов: 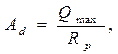
где Qmax = 1066,86 кН – максимальная расчетная поперечная сила на опоре;
Rp= 33,6 кН/см2 – расчетное сопротивление смятию торцевой поверхности, принимаемое в зависимости от марки стали по табл. В.7 прил. В СП 16.13330.2011 «Стальные конструкции» или по табл. Б.15 прил. Б пособия.
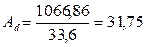 см2.
см2.
Для торцевого опорного ребра принимают ширину bd=b1f=18 см, где b1f – ширина сечения пояса в месте изменения сечения, см. Определяем толщину опорного ребра, исходя из требуемой площади смятия 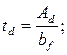
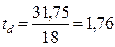 см, принимаем td = 18 мм.
см, принимаем td = 18 мм.
Площадь поперечного сечения принятого опорного ребра Ар=18*1,8= 32,4 см2 > Аd= 31,75 см2.
Вследствие недостаточных размеров ребра опорный участок стенки может потерять устойчивость из своей плоскости, поэтому его рассчитываем на продольный изгиб как стойку с расчетной длиной, равной высоте стенки 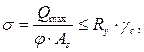
где 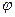 – коэффициент продольного изгиба стойки с гибкостью
– коэффициент продольного изгиба стойки с гибкостью 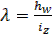 , устанавливаемый в зависимости от приведенной гибкости стенки
, устанавливаемый в зависимости от приведенной гибкости стенки 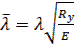 по данным табл. Д.1 прил. Д СП 16.13330.2011 «Стальные конструкции» или по табл. Б.16 прил. Б пособия, определяем тип кривой устойчивости – тип «с»;
по данным табл. Д.1 прил. Д СП 16.13330.2011 «Стальные конструкции» или по табл. Б.16 прил. Б пособия, определяем тип кривой устойчивости – тип «с»;
iz – радиус инерции сечения условной стойки относительно оси z, который определяют по формуле 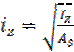 ;
;
 – момент инерции сечения относительно оси z без учета момента инерции стенки, определяемый по формуле
– момент инерции сечения относительно оси z без учета момента инерции стенки, определяемый по формуле 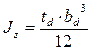 ;
;
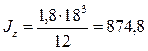 см4
см4
As – площадь условного таврового сечения, включающая опорные ребра и полосу стенки шириной S, зависящей от толщины стенки балки 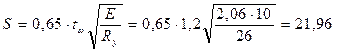 см, равная
см, равная
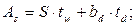
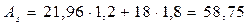 см2;
см2;
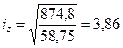 см2;
см2; 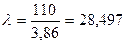 .
.
При λ=28,497 приведенная гибкостьˉλ=28,497*0,0355=1,01; тогда коэффициент продольного изгиба φ=0,901.
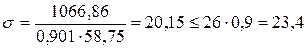 кН/см2.
кН/см2.
20,15 кН/см2 < 23,4 кН/см2 – условие выполняется, прочность опорного ребра достаточна.
Далее рассчитывается прикрепление опорного ребра к стенке балки сварными двухсторонними швами с помощью полуавтоматической сварки проволокой Св-08А.
Предварительно необходимо произвести расчет параметров сварных швов и определить минимальное значение βRw
Rwf=18 кН/см2 (по табл. Б.14); Rwz=0,45* Run=0,45*38= 17,1 кН/см2 (по табл. Б.7 и Б.3); βf=0,9 и βz=1,05 (по табл. Б.13).
Тогда βf* Rwf=0,9*18=16,2 кН/см2 < βz* Rwz=1,05*17,1= 17,955 кН/см2.
Катет сварных швов определяется, исходя из условия их прочности и максимально допустимой длины N/(2 βf kf Rwf)=85 βf kf см
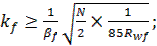 kf=1/0,9*√(1066,86/(2*85*18))=0,65 см.
kf=1/0,9*√(1066,86/(2*85*18))=0,65 см.
На основании выполненных расчетов kf=8 мм, что больше kfmin=7 мм (по табл. Б.12). Проверяем длину расчетной части шва
lw=85 βf kf=85 * 0,9 * 0,8= 61,2 см < hw=110 см, условие выполняется. Ребро привариваем к стенке балки по всей высоте сплошными угловыми швами с kf=8 мм.
Дата добавления: 2021-10-28; просмотров: 617;











