Основное уравнение теории удара

Основные положения и понятия теории удара

В предыдущих главах изучалось движение материальных объектов под действием сил, которые, действуя на материальные объекты в течение определенного промежутка времени, имели конечную величину. Изменение скорости материальных объектов происходило при этом непрерывно, то есть каждому элементарному промежутку времени соответствовало элементарное приращение скорости.

В данной главе рассматривается движение под действием таких сил, которые, действуя на материальный объект в течение весьма малого промежутка времени t, достигают больших величин (порядка 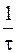), и при этом скорости точек материального объекта изменяются за этот малый промежуток времени на конечную величину.

Определение: Явление, при котором за малый промежуток времени, т.е. почти мгновенно, скорости точек материальных объектов изменяются на конечные величины, называется явлением удара.

Явление удара имеет место, если движущийся материальный объект сталкивается с другим движущимся или покоящимся объектом (добыча руды, футбол, ударные музыкальные инструменты), а также, если при движении СМТ внезапно появляются или исчезают новые связи (например, взрыв).

Так как при ударе конечное изменение скоростей происходит за весьма малый промежуток времени, то при этом возникают очень большие ускорения, а, следовательно, и очень большие силы. Эти силы действуют в течение весьма малого промежутка времени, но их импульсы за этот промежуток времени являются конечными величинами.

Определения:

Силы, возникающие при ударе в течение малого промежутка времени, но достигающие при этом большой величины, так что их импульсы за этот промежуток времени являются конечными величинами, называются ударными силами.

Малый промежуток времени, в течение которого длится удар, называется временем удара.

Импульсы ударных сил за время удара называются ударными импульсами.

Основное уравнение теории удара

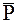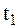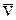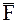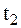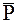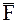Пусть дана МТ массы m, которая движется под действием обычной (неударной) силы . В момент , когда рассматриваемая МТ имеет скорость – скорость до удара, на нее начинает действовать ударная сила , действие которой прекращается в момент . Определим движение МТ под действием сил и за время удара .

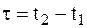Применяя теорему об изменении количества движения МТ (1.15), получим:

,

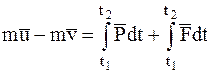где 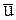– скорость точки в момент 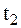после удара.

Рассмотрим отдельно каждый член правой части этого равенства. По теореме о среднем значении определенного интеграла можно написать:

,

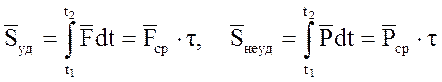где 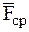и 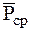есть средние значения сил 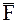и 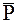в некоторый промежуток времени. При этом 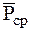является конечной величиной; ударная сила 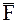за время удара 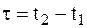достигает весьма большой величины 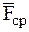(порядка 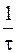). Поэтому произведение 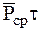будет пренебрежимо мало по сравнению с произведением 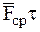, являющимся величиной конечной. Импульс 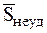обычной (неударной) силы 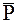за время удара t будет по сравнению с импульсом 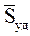ударной силы 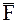очень мал и им можно пренебречь.

.

Окончательно получим:

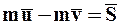. (8.1)

Основное уравнение теории удара: Изменение количества движения МТ за время удара равно действующему на эту МТ ударному импульсу.

Проектируя векторное равенство (8.1) на координатные оси, получим три следующих уравнения:

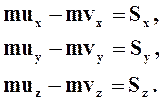(8.2)

Итак, изменение проекции количества движения материальной точки на какую-нибудь неподвижную ось за время удара равно проекции на ту же ось действующего на эту точку ударного импульса.

Уравнение (8.1) – основное уравнение теории удара, которое играет такую же роль в явлении удара, как второй закон динамики при изучении движений под действием обычных сил.

Определим перемещение МТ за время удара.

Так как 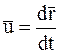, где 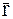– радиус-вектор, определяющий положение данной МТ относительно некоторой системы отсчета, то уравнение (8.1) можно записать следующим образом:

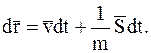
Проинтегрировав это равенство в пределах от 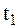до 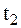, найдем:

,
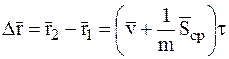где 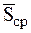есть среднее значение ударного импульса за время удара 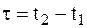. Учитывая при этом, что 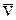и 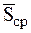суть величины конечные, а 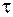- весьма мало, приходим к выводу, что 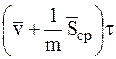будет близко к нулю и, следовательно, за время удара перемещение МТ 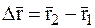практически равно нулю.

Таким образом, перемещением МТ за время удара можно пренебречь, считая, что за время удара эта МТ практически остается неподвижной, то есть не успевает переместиться.