МТ переменной массы – уравнение Мещерского

Найдем уравнение движения МТ массы М, которая непрерывно убывает, рассматривая ее как МТ переменной массы. Будем изучать движение этой МТ относительно некоторой неподвижной системы координат Oxyz (рис. 46).

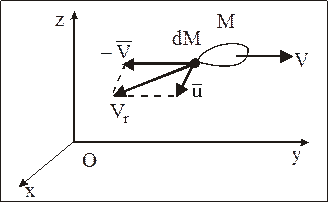
Рис. 46

Рассмотрим в некоторый момент времени t МТ переменной массы и отделяющуюся от нее в течение промежутка времени dt частицу, как одну МС, тем самым исключив внутренние силы. Таким образом, изучение движения МТ переменной массы, по существу, приводится к изучению движения МС.

Обозначим в момент времени t через 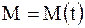всю массу МТ переменной массы. Пусть абсолютная скорость этой МТ в момент времени t будет 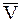, и, следовательно, количество ее движения в этот момент времени

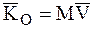. (7.1)

Пусть МТ переменной массы за промежуток времени dt отбросила от себя некоторую частицу и пусть абсолютная скорость этой частицы будет 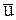. Масса отбрасываемой частицы равна величине 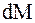, на которую за промежуток времени dt изменится масса МТ. Так как М – функция убывающая, то 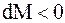и, следовательно, 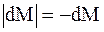. Количество движения рассматриваемой МС (МТ и отброшенная частица) в момент времени 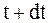будет:

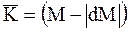
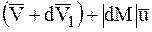, или

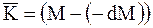
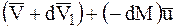, (7.2)
где 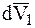– приращение скорости 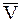МТ переменной массы, вызванное отбрасыванием от нее частицы массы .

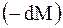Если на рассматриваемую МС не будут действовать внешние силы, то тогда, как известно, будет иметь место закон сохранения количества движения этой системы:

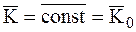
и на основании формул (7.1) и (7.2) будем иметь:

.

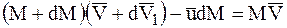Пренебрегая членом второго порядка малости ­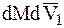 , получим:

.

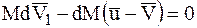Отсюда находим:

,

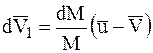где 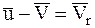есть относительная скорость (скорость по отношению к МТ переменной массы) отбрасываемой частицы.

Приращение 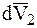скорости 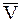МТ переменной массы, обусловленное действием на нее внешней силы 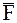, на основании второго основного закона динамики можно с той же точностью определить по формуле:

.

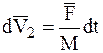На основании четвертого закона динамики о независимости действия сил суммарное приращение скорости 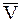будет:

.

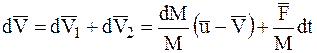Умножив на М и разделив на 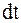обе части полученного равенства, получим:

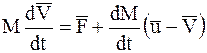, (7.3)

или

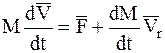, (7.4)

где 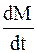– скорость изменения массы.

Уравнения, аналогичные соотношениям (7.3) и (7.4), могут быть получены и для случая присоединения массы.

Уравнение (7.3) или (7.4) представляет собой в векторной форме дифференциальное уравнение движения МТ переменной массы или уравнение Мещерского.

Вторые слагаемые правой части соотношений (7.3), (7.4) называются реактивной силой :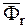

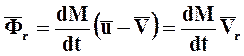. (7.5)

Учитывая соотношение (7.5), уравнение (7.3) или (7.4) –уравнение Мещерского, можно представить в виде:

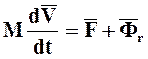(7.6)

Закон движения МТ переменной массы: Для каждого момента времени произведение массы МТ на ее ускорение равно геометрической сумме действующих на МТ внешней и реактивной сил.