Плоскопараллельного движения НМС

Предположим, что НМС под действием системы внешних сил 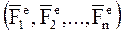совершает плоскопараллельное движение, при котором все точки НМС движутся в плоскостях, параллельных некоторой неподвижной плоскости, в качестве которой примем координатную плоскость xOy (рис. 45).

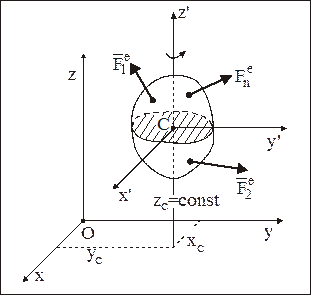
Рис. 45

Из кинематики (Ч.1 Кинематика) известно, что для определения положения НМС, совершающего плоскопараллельное движение, достаточно задать положение какой-нибудь его МТ, принятой за полюс, и угол поворота НМС вокруг оси, проходящей через этот полюс и перпендикулярной к неподвижной плоскости, параллельно которой происходит движение всех МТ рассматриваемого НМС. Задачи динамики решаются проще, если за полюс взять центр масс С и определять положение НМС координатами 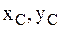центра масс и углом поворота j НМС вокруг оси 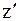, проходящей через центр масс С и перпендикулярной к плоскости xOy.

Таким образом, для изучения плоскопараллельного движения свободного НМС достаточно составить три дифференциальных уравнения, связывающих величины 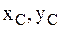и j с действующими на НМС внешними силами. Для описания движения центра масс воспользуемся первыми двумя уравнениями движения центра масс (6.1). Добавляя к ним уравнения вида (6.3) относительно оси Сz, получаем дифференциальные уравнения плоскопараллельного движения НМС:

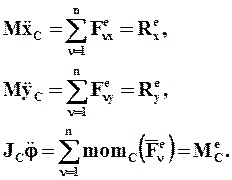(6.11)

Дифференциальные уравнения плоскопараллельного движения НМС могут быть записаны и в другой форме, если воспользоваться теоремой об изменении кинетической энергии НМС.