Лабораторная работа№10
 Определение концентрации растворов фотоэлектрическим концентрационным колориметром.
Определение концентрации растворов фотоэлектрическим концентрационным колориметром.
Цель работы: изучить устройство фотоэлектрического концентрационного колориметра и освоить колориметрический метод определения концентраций и оптических плотностей жидкостных растворов.
Приборы: фотоэлектрический концентрационный колориметр КФП-2МП, эталонные и исследуемый растворы CuSO4.
Т Е О Р И Я.
Пусть через однородное вещество распространяется пучок параллельных световых лучей. Выделим в веществе бесконечно тонкий слой dх (рис. 1), ограниченный параллельными поверхностями, перпендикулярными к лучам. Плотность потока энергии при прохождении света сквозь этот слой изменяется на величину –dI ( знак «минус» говорит о том, что плотность потока энергии уменьшается).
Явления поглощения света веществом объясняется с точки зрения электромагнитной теории света следующим образом. Падающая на вещество электромагнитная световая волна имеет частоту 1014 – 1015 Гц. С такой частотой в веществе смогут колебаться только электроны, так как ионы слишком велики и при таких частотах не успевают смещаться под действием переменного электромагнитного поля. В результате колебания электронов возникают вторичные электромагнитные волны той же частоты: отраженные и преломленные, частично же энергия падающей электромагнитной волны переходит в энергии движения атомов, т.е. во внутреннюю энергию вещества. Вынужденные колебания электронов, а следовательно и поглощение света, становятся особенно интенсивными при резонансной частоте.
Поглощением света называется уменьшение энергии световой волны, происходящее по мере проникновения ее вглубь вещества. Для количественной оценки поглощения света введем понятие интенсивности света (I). Интенсивностью света или плотностью потока энергии назовем количество энергии ежесекундно переносимое светом через единицу поверхности, расположенной перпендикулярно к лучам
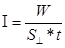 , (1) W – лучистая энергия
, (1) W – лучистая энергия
S^ - площадь, на которую падают электромагнитные волны
t – время прохождения волны.
Закон поглощения света веществом можно вывести не рассматривая внутреннего механизма взаимодействия света с веществом.
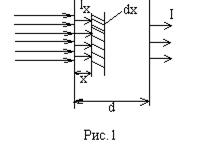
Очевидно, dI пропорционально плотности потока энергии Iх, принесенного волной к данному слою, а также толщине слоя вещества dx, т.е.
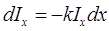 . (2)
. (2)
 Коэффициент kl зависит от длины световой волны, падающего света и химической природы поглощающего вещества, и называется коэффициентом поглощения. Пусть а – полная толщина слоя вещества. Iо и I – плотность потока энергии, падающей на вещество и вышедшей из него. Уравнение (2) – дифференциальное уравнение с разделяющимися переменными. Перенесем Iх в уравнении (2) в левую часть и проинтегрируем полученное выражение
Коэффициент kl зависит от длины световой волны, падающего света и химической природы поглощающего вещества, и называется коэффициентом поглощения. Пусть а – полная толщина слоя вещества. Iо и I – плотность потока энергии, падающей на вещество и вышедшей из него. Уравнение (2) – дифференциальное уравнение с разделяющимися переменными. Перенесем Iх в уравнении (2) в левую часть и проинтегрируем полученное выражение
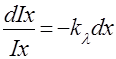
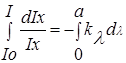
получим
lnIo – lnI = -kla
Это экспоненциальный закон поглощения света – закон Бугера.
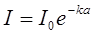 (3)
(3)
Коэффициент поглощения кl - это величина, обратная толщине слоя а, на котором интенсивность света уменьшается в е раз. Коэффициент поглощения в области видимого света для воздуха кl = 10-6см-1 , для воды 2·10-3см-1, для металлов кl имеет порядок десятков тысяч – 103-104см-1.
Большое значение для медицины имеет изучение поглощения света в растворах. В этом случае поглощение зависит также и от концентрации вещества в растворе. Закон поглощения с учетом концентрации раствора, называемый законом Бугера-Ламберта-Бера, записывается в виде:
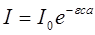 , (4)
, (4)
где e - молекулярный коэффициент поглощения (к=eс), зависящий от природы молекул растворенного вещества, от длины волны света и температуры раствора; с - концентрация раствора; а – толщина слоя раствора. Закон Бугера-Ламберта-Бера (4) справедлив при условии, что растворитель не поглощает света данной длины волны и раствор имеет невысокую концентрацию.
Для некоторых практических расчетов наиболее удобно выражение закона Бугера (3) через десятичные логарифмы
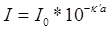 (5)
(5)
 |
Ясно, что коэффициенты кl и к¢l cвязаны: к¢l = 0,1 кl, произведение к¢lа называется оптической плотностью слоя вещества (D), т.е. D= к¢lа, а отношение I/Io называется пропусканием (Т).
Из (5) получаем
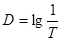 , (6)
, (6)
При оптической плотности D= 1 пропускание Т = 0,1 = 10%, при оптической плотности D= 2 пропускание Т = 0,01 = 1% и т.д. с увеличением оптической плотности пропускание света уменьшается по закону, выраженному соотношением (6).
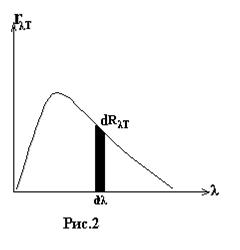
Диэлектрики слабо поглощают свет. В диэлектрике все электроны связаны: они колеблются с собственной частотой w0 и «раскачать» их падающей волне трудно. Однако в том случае, когда частота падающей световой волны w близка к частоте собственных колебаний электрона w»w0 (резонанс), амплитуда вынужденных колебаний резко возрастает, возрастает и коэффициент поглощения. Таким образом, поглощение света в диэлектрике имеет селективный (избирательный) характер (рис. 2)

Зависимость кl от l представляет собой кривую с рядом максимумов: максимумы представляют собой полосы поглощения веществом света для определенного интервала длин волн. Например «красным» является стекло, слабо поглощающее красные и оранжевые лучи, и хорошо поглощающие синие, зеленые и фиолетовые лучи. Если красное стекло осветить синим светом, то оно будет казаться «черным», т.к. синие лучи хорошо поглощаются красным спектром. Зависимость оптической плотности (или коэффициента поглощения) вещества (например, раствора) от длины волны l называется спектральной характеристикой вещества (раствора).
Для измерения оптической плотности вещества, концентрации растворов и для изучения спектральной характеристики растворов используется прибор, называемый фотоэлектрический концентрационный колориметр. Колориметр позволяет производить также измерения коэффициентов пропускания рассеивающих взвесей, эмульсий и коллоидных растворов в проходящем свете.
Устройство и работа колориметра.
Принцип действия колориметра основан на поочередном измерении светового потока Фо=Wо/t, прошедшего через растворитель, по отношению к которому производится измерение, и потока Ф=W/t, прошедшего через исследуемую среду.
Световые потоки Фо и Ф фотоприемниками преобразуются в электрические сигналы Ио и И, которые обрабатываются микро-ЭВМ колориметра и представляются на цифровом табло в виде коэффициента пропускания, оптической плотности, концентрации.
С помощью микро-ЭВМ рассчитывается коэффициент пропускания Т исследуемого раствора по формуле
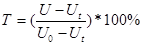 (7)
(7)
Где Ut – величина сигнала при перекрытом световом потоке.
Оптическая плотность исследуемого раствора рассчитывается по формуле:
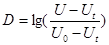 (8)
(8)
Измерение концентрации исследуемого раствора на колориметре возможно при соблюдении основного закона светопоглощения, т.е. при линейной зависимости оптической плотности D исследуемого раствора от концентрации (см(5') и (4) ).
Концентрация исследуемого раствора рассчитывается по формулам:
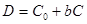 , (9)
, (9)
где Со и b – коэффициенты, определяемые по градуировочной характеристике.
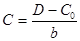 (10)
(10)
Градуировочная характеристика составляется исследованием по набору растворов с известной концентрацией.
Устройство колориметра.
Общий вид колориметра изображен на рис.3. Колориметр состоит из колориметрического 1 (рис.3) и вычислительного 2 блоков и блока питания. На задней панели колориметра имеется электрошнур с вилкой для включения в сеть, предохранитель и выключатель сетевого напряжения (тумблер).

Рис.3.
В световой пучок светофильтры вводятся ручкой 6 (рис.3). Рабочее положение каждого светофильтра фиксируется.
5 – кюветное отделение, ввод в световой пучок одной или другой кюветы осуществляется поворотом ручки 4 (рис.3) до упора влево или вправо (положение «1» или «2»). В положении «1» в световой пучок вводится кювета с растворителем, в положении «2» – в световой пучок вводится кювета с исследуемым раствором. Кюветное отделение закрывается крышкой 5.
При открытой крышке кюветного отделения шторка перекрывает световой пучок.
Переключение фотоприемников осуществляется с помощью ручки 3 (рис3).
Блок вычислений
В вычислительный блок 2 (рис.3) входит система микро - процессорная (МПС) «Электроника МС2703».
На передней панели МПС расположена клавиатура, цифровое табло и два сигнальных светодиода. Клавиатура состоит из 24 клавиш. Клавиша «Пуск» предназначена для запуска микропроцессорной системы. Клавиши «b» и «С» предназначены для вызова на цифровое табло из памяти МПС значений соответствующих коэффициентов для их контроля и ввода новых значений. Клавиша «СБР» предназначена для стирания значения вызванного коэффициента (в случае необходимости задания нового значения).
Клавиши «0», «1-9», «-», «,» предназначены для набора на цифровом табло МПС нового значения коэффициентов «b» и «С» = Со.
Клавиша «УТВ» предназначена для записи в память МПС нового значения коэффициента «В» или «С», набранного на цифровом табло.
Клавиши «К(1)», «t(2)», «Д(5)» предназначены для выполнения калибровки прибора, измерений коэффициента пропускания, оптической плотности исследуемого вещества, концентрации вещества в растворе.
Клавиша «А(3)» предназначена для измерения активности.
Клавиша «Ц/Р» предназначена для перевода МПС в один из двух режимов выполнения измерений: режим одиночных измерений и режим циклических измерений. В режиме одиночных измерений измерения, выполняются один раз при нажатии соответствующей клавиши; в режиме циклических измерений первое измерение производится при нажатии соответствующей клавиши и затем повторяется циклически с периодом 5с до тех пор, пока МПС не будет переведена в режим выполнения одиночных измерений. Перевод МПС из режима циклических измерений в режим одиночных и обратно происходит при нажатии клавиши Ц/Р. Сигнальный светодиод «Ц» и сигнальный светодиод «Р» служат для определения режима измерения, в режиме одиночных измерений горит светодиод «Р», в противном случае горит светодиод «Ц». Цифровое табло состоит из 6-ти индикаторов. Первый индикатор служит для отображения одного из символов «3», «2», «1», «4», «5», «0» появляющегося при нажатии одной из клавиш «А(3)», «t(2)», «К(1)», «С(4)», «Д(5)» соответственно и при измерении «нулевого отсчета» n0.
Индикаторы 2-6 служат для вывода результатов измерений и значений параметров «С» и «b».
Клавиша «Ш(0)» МПС предназначена для проверки (измерения) «нулевого отсчета» n0.
Порядок работы.
1.Снятие спектральной характеристики раствора.
Для того, чтобы построить кривую зависимости оптической плотности раствора от длины световой волны (спектральная характеристика раствора) нужно определить оптическую плотность данного раствора в различных участках спектра, выделяемых светофильтрами колориметра. Светофильтры в ход световых лучей вводятся ручкой 6 (рис.3).
При измерении со светофильтрами 315, 340, 400, 440, 490, 540 нм ручку 3 (рис.3) установить в положение «315-540».
При измерении со светофильтрами 590, 670, 750 и т.д. ручку 3 (рис.3) установить в положение «590-980».
После смены светофильтра, а также после нахождения колориметра при открытой крышке кюветного отделения длительное время (более 5 мин.), измерения начинают после 5-ти минутной выдержки фотоприемника в освещенном состоянии, т.е. при закрытой крышке кюветного отделения.
1. Подсоединить колориметр к сети 220 В. Открыть крышку кюветного отделения и включить тумблер «Сеть», при этом должна загореться сигнальная лампочка (на цифровом табло могут появиться различные символы).
2. Нажать клавишу «Пуск» – на цифровом табло появится мигающая запятая и горит индикатор «Р». Если запятая не появилась – повторно нажмите клавишу «Пуск». Выдержать колориметр при включенном состоянии в течение 15 минут при открытой крышке кюветного отделения. Измерение и учет «нулевого отсчета» n0 производится при помощи клавиши «Ш(0)» МПС. Перед измерением «нулевого отсчета» n0 крышку кюветного отделения закрыть и открыть. По истечении 5с нажать клавишу «Ш(0)». На цифровом табло справа от мигающей запятой высвечивается значение п0 , а слева – символ «0». Значение n0 должно быть не менее 0.001 и не более 1.000.
3. В кюветное отделение установить кюветы с растворителем и исследуемым раствором. Кювету с растворителем установить в дальнее гнездо кюветодержателя, а кювету с исследуемым раствором в ближнее гнездо кюветодержателя. Ручкой 6 установить необходимый светофильтр, ручкой 3 – нужный фотоприемник (рис. 3). Начинают со светофильтра 315 нм.
4. Ручку 4 (рис.3) установить в положение «1» (в световой поток вводится кювета с растворителем).
5. Закрыть крышку кюветного отделения, нажать клавишу «К(1)». На цифровом табло слева от мигающей запятой загорается символ «1».
6. Затем ручку 4 (рис.3) установить в положение «2» (в световой пучок вводится кювета с исследуемым раствором).
7. Нажать клавишу «Д(5)». На цифровом табло слева от мигающей запятой появляется символ «5», означающий, что произошло измерение оптической плотности. Отсчет на цифровом табло справа от мигающей запятой соответствует оптической плотности исследуемого раствора.
8. Операцию по п-п 4-7 повторить 3 раза. Оптическую плотность определить как среднее арифметическое из полученных значений.
9. Ручкой 6 (рис.3) установить следующий светофильтр.
10. Повторить операции 4-9.
11. Светофильтры меняют от 315 до 740 нм (при включении светофильтра 590 нм переключите фотоприемник ручкой 3).
12. Строят кривую зависимости оптической плотности раствора от длины волны, которая является спектральной характеристикой данного раствора.
2. Определение концентрации раствора медного купороса.
При измерении концентрации вещества в растворе следует соблюдать следующую последовательность в работе:
выбор светофильтра;
выбор кюветы;
построение градуированного графика для данного вещества и определения коэффициентов «С» и «b»;
введение коэффициентов «С» и «b» в память вычислительного блока;
измерение концентрации вещества.
§ 1. Выбор светофильтра
На графике зависимости оптической плотности раствора от длины волны, полученном в 1-ом упражнении, отметить тот участок кривой, для которого выполняются следующие условия:
а) оптическая плотность имеет максимальную величину;
б) ход кривой примерно параллелен горизонтальной оси, т.е. оптическая плотность мало зависит от длины волны (для некоторых растворов это условие может на выполнятся, тогда при выборе светофильтра ограничиваются выполнением первого условия).
Светофильтр для работы выбрать так, чтобы длина волны приходилась на отмеченный выше участок спектральной кривой испытуемого раствора.
§ 2. Выбор кюветы.
Относительная погрешность измерения оптической плотности раствора достигает минимума при значении оптической плотности 0.4. Поэтому при работе на колориметре рекомендуется путем соответствующего выбора кювет, работать вблизи указанного значения оптической плотности.
1. Предварительный выбор кювет проводится визуально, соответственно интенсивности окраски раствора. Если раствор интенсивно окрашен (темный), следует пользоваться кюветами с длиной 1-3 мм. В случае слабо окрашенных растворов рекомендуется работать с кюветами с большой длиной (30-100 мм).
В предварительно подобранную кювету налить раствор средней концентрации (допустим у Вас растворы 1%, 2%, 5% и 10%, то нужно взять 5% раствор) и измерить его оптическую плотность, введя в ход лучей соответствующий светофильтр, выбранный в §1. Если полученное значение оптической плотности составляет примерно 0,3-0,5, то можно выбрать данную кювету для работы.
§ 3. Построение градуированного графика для данного вещества и определение коэффициентов «С» и «b».
1. Приготовить ряд растворов данного вещества с известными концентрациями.
2. Измерить оптические плотности всех известных растворов и построить градуированный график, откладывая по горизонтальной оси известные концентрации, а по вертикальной – соответствующие им значения оптической плотности.
3. По градуированному графику определить коэффициенты «с» и «b»
«С»=Со – значение оптической плотности при С=0, т.е. при пересечении градуированного графика с осью оптической плотности Д
 |
где a - угол между градуированной прямой и осью концентраций Сi
Сi и Дi – текущая точка градуированного графика.
4. Ввести в память вычислительного блока коэффициенты «С» и «b». Для этого нажать клавиши «С» («b»), СБР, на цифровом табло высвечивается символ «С» («b») слева от мигающей запятой, набрать с помощью клавиатуры значение коэффициента «С» («b»). На цифровом табло справа от мигающей запятой высвечивается значение коэффициента. Затем нажать клавишу УТВ – информация на цифровом табло исчезнет.
5. В кюветное отделение установить кювету с исследуемым раствором. Ручку 4 (рис. 4) установить в положение «1», закрыть кюветное отделение, нажать клавишу «К(1)», на цифровом табло слева от мигающей запятой загорается «1», затем ручку 4 (рис. 4) установить в положении «2».
6. Нажать клавишу «С(4)». На табло слева от мигающей запятой появляется символ «4», означающий, что произошло измерение концентрации исследуемого раствора.
7. П. 5-6 повторить 3 раза, концентрацию исследуемого раствора найти как среднее арифметическое.
Контрольные вопросы.
1. Дайте определение интенсивности света.
2. Выведите закон Бугера.
3. Объясните физический смысл коэффициента поглощения.
4. Напишите закон Бугера-Ламберта-Бера, поясните величины, входящие в формулу.
5. Расскажите о назначении светофильтров.
6. Как изменяется величина пропускания Т при увеличении оптической плотности вещества.
7. За счет чего можно увеличить оптическую плотность раствора.
8. Для каких длин волн оптическая плотность раствора будет максимальной.
9. Объясните процесс поглощения с молекулярной точки зрения.
Лабораторная работа N11
ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ СТЕФАНА – БОЛЬЦМАНА ПРИ ПОМОЩИ ОПТИЧЕСКОГО ПИРОМЕТРА.
Цель работы: 1. Ознакомиться с законами теплового излучения.
2. Научиться измерять температуру раскаленных тел.
3. Подсчитать постоянные Стефана-Больцмана и
Планка.
Приборы: оптический пирометр с исчезающей нитью, лампа накаливания, источник питания.
ВВЕДЕНИЕ.
Излучение телами электромагнитных волн (свечение тел) может осуществляться за счет различных видов энергии. Самыми распространенными являются свечения тел, обусловленные их нагреванием. Этот вид свечения называют тепловым. Тепловое излучение имеет место при любой температуре, но при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны. Тепловое излучение является единственным видом излучения, которое может находиться в равновесии с излучающими телами. Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при повышении температуры.
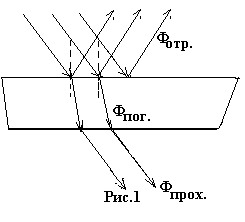
Предположим, что на какое-нибудь тело (рис.1) падает поток излучения Ф0. Часть этого потока Фотр. отражается от поверхности обратно, часть потока при небольшой толщине тела пройдет и за телом будет наблюдаться поток излучения Фпрох., часть потока поглотится и превратится в другие энергии ( в конечном счете в тепло ). Составим уравнение энергетического баланса
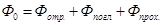 . (1)
. (1)
Разделив на Ф0, получим сумму безразмерных коэффициентов
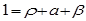 , (2)
, (2)
где r=Фотр/Ф0 -коэффициент отражения, а=Фпогл / Ф0 -коэффициент поглощения, b=Фпрох /Ф0 -коэффициент пропускания.
При достаточной толщине любое тело становиться непрозрачным, поэтому ограничиваемся случаем, когда b=0, тогда
r+a=1. (3).
Коэффициенты отражения и поглощения, как отражательная и поглощательная способность тела однозначно связаны друг с другом, зависят от строения и состояния тела, от характера обработки поверхности. Кроме того, максимальный эффект отражения и поглощения электромагнитных волн, падающих на тело, наблюдается в области резонансных частот (в области совпадения собственных частот колебаний электрических зарядов составляющих тело, с частотой падающей электромагнитной волны). Следовательно, отражательная и поглощательная способность тела являются функциями длины волны l, а также абсолютной температуры тела Т. Итак:
rlT +alT=1 (4)
Рассмотрим частные случаи. Пусть тело полностью отражает все падающие на него лучи, т.е. аlТ=0 и rlТ=1.Такое тело называем абсолютно белым и оно окрашено в цвет луча, которым освещено. Так, белое платье, освещенное лучом розового цвета, кажется розовым.
Если rl,Т  =0 , а alТ=1, то тело поглощает все падающие на него лучи, такое тело называется абсолютно черным. Примером является сажа, для нее al,Т = 0,99. И, наконец, тело, для которого поглощательная способность меньше 1, но постоянна во всем интервале длин волн, называется серым:
=0 , а alТ=1, то тело поглощает все падающие на него лучи, такое тело называется абсолютно черным. Примером является сажа, для нее al,Т = 0,99. И, наконец, тело, для которого поглощательная способность меньше 1, но постоянна во всем интервале длин волн, называется серым:
al,Т=const<1
ЭНЕРГЕТИЧЕСКАЯ СВЕТИМОСТЬ. ЛУЧЕИСПУСКАТЕЛЬНАЯ СПОСОБНОСТЬ. ЗАКОН КИРХГОФА.
Как уже отмечалось, тела наряду с отражением и поглощением способны испускать электромагнитные волны. Интенсивность теплового излучения принято характеризовать величиной потока энергии, испускаемого единицей поверхности излучающего тела во всех направлениях:
РРрR RТ=Е/St, (5)
где E- излучаемая энергия, S- излучаемая поверхность, t- время излучения. Величину Rт- называют энергетической светимостью и она является функцией температуры. Излучение состоит из волн различных частот n или длин волн l. Обозначим поток энергии, испускаемый единицей поверхности тела в интервале длин l¸l+dl , через dRl,т.
При малом интервале dl поток dRl,Т будет пропорционален
dRl,Т= rl,Т dl. (6) 
Величина rl,Т называется спектральной плотностью энергетической светимости или лучеиспускательной способностью. Длины волн меняются для электромагнитного излучения от нуля до бесконечности, следовательно:
RТ= 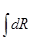 l,Т =
l,Т = 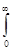 rl,Тdl (7)
rl,Тdl (7)
Вид спектральной характеристики теплового излучения – лучеиспускательной способности то длины волны – приведен на рис. 2, для некоторой температуры Т. Энергетическая светимость RТ на рис.2 – это площадь под кривой.
Спектральной характеристикой теплового излучения является и поглощательная способность тела al,Т. Поглощательная способность тела показывает какая доля энергии излучения Е, падающая за единицу времени на единицу площади поверхности тела в интервале длин волн от l до l+ dl поглощается телом.
al,Т=Епогл/ Е, (8)
где Епогл- энергия, поглощенная телом.
Величина лучеиспускательной rl,Т и поглощательной al,Т способностей отдельно взятые, могут меняться при переходе от одного тела к другому, даже если тела находятся при одинаковых условиях, но отношение rl,Т /al,Т не зависит от материала тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры: 
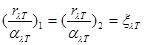 , (9)
, (9)
где индексы 1, 2 относятся к разным телам.
Для абсолютно черного тела al,Т =1, следовательно rl,Т для такого тела равна xlT. Таким образом, универсальная функция Кирхгофа xlT есть не что иное, как лучеиспускательная способность абсолютно черного тела. Выражение (9) носит название закона Кирхгофа.
ЗАКОНЫ СТЕФАНА – БОЛЬЦМАНА И ВИНА.
Теоретическое объяснение законов излучения абсолютно черного тела имеет огромное значение в развитии физики – оно привело к понятию квантов энергии.
Главной проблемой теории теплового излучения было нахождение функции xl,Т. Стефан (1879) из анализа экспериментальных данных пришел к выводу, что энергетическая светимость RТ любого тела пропорциональна четвертой степени температуры. Больцман (1884г) теоретически, исходя из принципов равновесной термодинамики, показал, что выводы Стефана применимы только для абсолютно черного тела.
RТ = 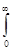 rl,Тdl =
rl,Тdl = 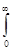 xl,Тdl = sТ4. (10)
xl,Тdl = sТ4. (10)
Таким образом, энергетическая светимость абсолютно черного тела пропорциональна четвертой степени температуры.
RТ = s Т4, (10а)
это математическое выражение закона Стефана – Больцмана
s = 5.67 * 10-8Дж/м2 с К4 называют постоянной Стефана-Больцмана.
Используя не только термодинамические законы, но и электромагнитную теорию, Вин (1893г.) установил вид функции спектральной плотности энегретической светимости абсолютно черного тела
xl,Т = 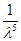 ·y (l,Т), (11)
·y (l,Т), (11)
где y (l,Т) - некоторая функция зависящая от произведения l·Т. Функция xl,Т имеет максимум при некоторой длине волны l0 т.е. при этой длине волны
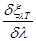 = 0
= 0
Длина волны l0 , на которую приходится максимум лучеиспускательной способности, связана с абсолютной температурой излучающего тела соотношением
l0· Т = В, (12)
где В =2,9 · 10-3м К
Из (12) получаем
l0 = 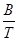 (13)
(13)
Это соотношение носит название закона Вина. Действительно, с ростом температуры излучателя, максимум лучеиспускательной способности смещается в область коротких длин волн.
 |
ФОРМУЛА ПЛАНКА.
Для объяснения законов теплового излучения М. Планк (1900г.) высказал гипотезу, что поглощение и испускание энергии электромагнитного излучения атомами и молекулами возможно только «порциями», которые стали называть квантами энергии. Величина кванта энергии
x = h n , (14)
где h - постоянная величина (постоянная Планка),которая равна = 6,62· 10-34Дж с., n - частота, излучаемого света.
На основе квантовых представлений Планк вывел аналитическое выражение функции xl,Т. Эта функция, получившая название функции Планка, имеет следующий вид:
 (15)
(15)
или
xn,Т = 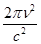 ·
· 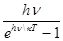 (16)
(16)
 При интегрировании выражения (15), (16) по всему спектру излучения, получим закон Стефана-Больцмана
При интегрировании выражения (15), (16) по всему спектру излучения, получим закон Стефана-Больцмана
RТ = 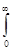 xn,Т·dn = s Т4.
xn,Т·dn = s Т4.
Если взять производную по l от функции(15) и ее приравнять к нулю, то получим закон смещения Вина
l0 = 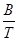
ИЗМЕРЕНИЕ ОЧЕНЬ ВЫСОКИХ ТЕМПЕРАТУР.
При измерении очень высоких температур, например, раскаленных тел, а также температур тел, удаленных от наблюдения (звезд), нельзя пользоваться обычными методами измерения температур (термометрами, термопарами). В этих случаях о температуре тела можно судить только по его излучению. Совокупность методов измерения высоких температур, основанных на законах теплового излучения, в частности, на использовании зависимости лучеиспускательной способности тела от его температуры, называется оптической пирометрией. Приборы, которые применяются в оптической пирометрии, называются пирометрами излучения.
Комплект оптического пирометра с исчезающей нитью состоит из зрительной трубы, миллиамперметра и аккумулятора. Схема его устройства показана на рис 4 и 5.
 |
На рис .4. а- тубус объектива зрительной трубы
в- тубус окуляра зрительной трубы
К- кольцо реостата
г – шкала миллиамперметра.
В фокусе объектива О (рис.5.) помещена электрическая лампочка Л с прямолинейной нитью. При помощи окуляра О1, наблюдается нить лампы и совмещенное с ней (при помощи объектива) изображение поверхности нагретого тела (источника света). Наблюдение ведется через красный светофильтр Ф, пропускающий узкую спектральную полосу длин волн в области 660 нм. При помощи реостата R накал нити лампы меняется так, чтобы нить на фоне излучающей поверхности исчезла. Этому моменту соответствует совпадение величин лучеиспускательной способности нити лампы и исследуемой поверхности в области длины волны l =660нм. Пирометр предварительно проградуирован по абсолютно черному телу.
Задачей данной работы является нахождение численного значения постоянной Стефана-Больцмана s и постоянной Планка h. .
В нашей работе нагретым телом, тепловое излучение которого используется для определения s, служит нить из нихрома обычной лампы накаливания. Для поддержания нити в нагретом состоянии к ней подводят мощность W = I*U. Некоторая часть 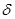 этой мощности расходуется на нагрев держателей нити, контактов и т.д., следовательно, мощность теряемая при тепловом излучении нити равна I*U (1-
этой мощности расходуется на нагрев держателей нити, контактов и т.д., следовательно, мощность теряемая при тепловом излучении нити равна I*U (1- 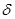 ) где I - ток, текущий через нить, а U - напряжение, под которым находится нить.
) где I - ток, текущий через нить, а U - напряжение, под которым находится нить.
Нагретое тело при температуре Т излучает энергию и поглощает излучение окружающей среды, находящейся при температуре Т. Мощность потребляемая нагретым телом от электрической сети, компенсирует потерю энергии на излучение, которая пропорциональна разности Т4 – Т04.
Учитывая все вышесказанное, можно записать соотношение
I*U (1 - 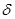 ) = s*Т4*S (17)
) = s*Т4*S (17)
Отсюда получаем рабочую формулу для вычисления
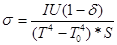 (18)
(18)
Для нихромовой нити 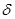 =0,25. Излучающая поверхность нихромовой спирали S=3*10-4м2.
=0,25. Излучающая поверхность нихромовой спирали S=3*10-4м2.
ПОРЯДОК РАБОТЫ:
1.Приготовить оптический прибор к проведению измерений: для чего а). Настраивают его так, чтобы в окуляре было четко видно изображение раскаленной нити. б)Для получения света одной длины волны вводят монохроматический (красный) светофильтр l = 0,65 мкм. Поворачивая кольцо окуляра В, и еще раз подлаживают фокусировку нити.
2.Накал нити можно изменять поворотом кольца реостата по часовой стрелке на БП-1, устанавливая токи накала нити I1=1,5А; I2=2,9А, и т.д.
3.Напряжение на нити равно 9В.
4.Направив объектив пирометра на раскаленную нить и передвигая тубус объектива, устанавливают на резкость изображение нити.
5.Увеличивают накал нити и измеряют ее температуру при данном накале. Для этого изменяют яркость нити эталонной лампы пирометра поворотом кольца реостата r до того момента, пока средний участок нити лампы не исчезнет на фоне раскаленной нити. В этот момент делают отсчет температуры по шкале пирометра.
6.Подставляют в формулу (18), измеренную температуру (t +273), комнатную температуру (t0 +273), площадь нити (указана в методическом пособии), величину тока I, напряжение U и вычисляют значение s.
7. Увеличивают ток накала нити и находят второе значение s, снимая соответствующие значения t, I.
8. Опыт повторяют 3 раза.
9. Из полученных значений s1, s2, s3 находят среднее значение.
Лабораторная работа №12
ИЗУЧЕНИЕ СПЕКТРА ВОДОРОДА И ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА.
Цель работы: измерить длины волн спектральных линий, лежащих в видимой части спектра атома водорода; вычислить постоянную Ридберга.
Приборы и принадлежности; призменный монохроматор УМ-2, водородная газоразрядная трубка, ртутная лампа, катушка Румкорфа.
1.Введение.
Опытами Резерфорда (1911г.) было установлено, что атом любого элемента состоит из положительно заряженного ядра, вокруг которого движутся (в первом приближении по круговым орбитам) электроны. Заряд ядра q=eZ, где Z- порядковый номер элемента в таблице Менделеева, е- заряд электрона. Т.к. атом электронейтрален, то число электронов в атоме равно Z и их суммарный заряд равен (-Ze). Почти вся масса атома сосредоточена в ядре.
Однако модель атома Резерфорда находится в противоречии с законами классической электродинамики. Дело в том, что движение электрона по круговой орбите – это движение с ускорением. Всякий же ускоренно движущийся заряд излучает электромагнитные волны, и его энергия вследствие этого должна непрерывно уменьшаться. В результате электрон должен упасть на ядро, а излучаемый спектр должен быть непрерывным.
Однако атомы стабильны и существуют длительное время, о чем свидетельствует существование окружающей нас реальности. Спектры же, излучаемые атомами различных элементов- линейчатые. Замечено, что спектральные линии расположены не беспорядочно, а объединяются в группы или серии линий. Четче всего это проявляется в спектре атома водорода, в котором выделяется несколько серий. Линии этих серий могут быть описаны сериальными формулами:
серия Лаймана 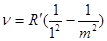 (m=2,3,4....)
(m=2,3,4....)
серия Бальмера 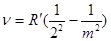 (m=3,4,5,...)
(m=3,4,5,...)
серия Пашена 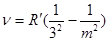 (m=4,5,6,....)
(m=4,5,6,....)
Серия Бальмера описывает видимую часть спектра атома водорода.
В 1913 году Бором были сформулированы постулаты, которые дали объяснение экспериментальным фактам:
1) электрон в атоме может вращаться только по строго определенным (стационарным) орбитам, радиус которых определяется из условия, что момент импульса электрона на этих орбитах равен целому кратному от 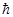 ,т.е.
,т.е.
2) 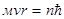 (1.1)
(1.1)
где 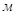 - масса электрона, v - его скорость, rрадиус боровской орбиты, r= 1,2,3,…- квантовые числа, определяющие номер орбиты, по которой движется электрон;
- масса электрона, v - его скорость, rрадиус боровской орбиты, r= 1,2,3,…- квантовые числа, определяющие номер орбиты, по которой движется электрон;
2) вращаясь по стационарным орбитам электрон не излучает;
3).излучение происходит лишь при переходе электрона из стационарного состояния с большим значением энергии Е1 в другое стационарное состояние с меньшим значением энергии Е2. При этом излучается квант света, частота которого n определяется из условия
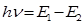 (1.2)
(1.2)
где hn - энергия излученного кванта.
Постулаты Бора объяснили линейчатый характер атомных спектров и дали возможность теоретически рассчитать спектр простейшего атома – атома водорода и водородоподобных ионов (т.е. ионов с одним электроном ), однако спектры более сложных атомов эта теория объяснить не могла. Затруднения теории Бора были преодолены квантовой механикой, показавшей неприменимость классических представлений к микрообъектам.
Вычислим радиусы стационарных орбит и полную энергию электрона в водородоподобном атоме, состоящим из ядра с зарядом +Ze и одного электрона с зарядом (–e).
Полная энергия Е электрона в атоме водорода складывается из кинетической энергии К и потенциальной энергии П взаимодействия электрона с ядром.
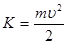 ;
; 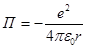

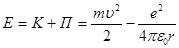
Дата добавления: 2017-10-04; просмотров: 2756;











