Поляризация света при отражении на границе изотропных диэлектриков

1.Поляризация при отражении от поверхности диэлект­рика.

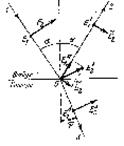
При рассмотрении поляризации света важно помнить, что электромагнитная волна –поперечна. Известно, что свет, отраженный от гладкой полированной поверхности диэлектриков (стекла, пластмассы, мрамора, поверхности воды и других жидкостей и т. д.), всегда частично, а иногда и полностью поляризован. Разберем физический смысл явления. Пусть на границу прозрачного диэлектри­ка, например, стекла (рис.6), падает луч естественного света. На границе он разделяется на два луча — отражен­ный и преломленный. Первый идет обратно в воздух под углом, равным углу падения, второй распространяется в стекле под углом преломления j к нормали, который связан с углом падения a следующим соотношением:

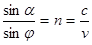, (5)

где с- скорость света в воздухе; v- скорость света в стекле; n- показатель преломления стекла.

Все возможные направления электрического вектора в естественном свете можно заменить совокупностью двух равных взаимно перпендикулярных компонент (см. раздел «Поляризация»). Пусть они расположены так: одна (Е2) —в плоскости падения луча (на рис.6 изображена черточкой) и вторая (Е1.) — перпендикулярно ей (от этой компоненты на рисунке 6 ви­ден только след в виде точки). Так как отра­женный и преломленный лучи представляют собой вторичные волны, которые возникли следствие электромагнитных колебаний, вызванных в атомах среды падающим светом, то вектор Е2 изменит свое направление, оставаясь перпендикулярным ходу преломленного луча (Е2¢) (электромагнитные волны – поперечны), Е1 перпендикулярен плоскости падения, поэтому в преломленном и отраженном лучах он будет направлен также как и в падающем (Е1¢).

Рис.6 Поляризация света при отражении	Рис. 7 Угол полной поляризации

При этом векторы Е1¢ и Е2 ¢ неравноправны по отношению к отраженному лучу, поэтому разложим вектор Е2 ¢ на ком­поненты Е2” и 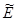2. В следствие поперечности световых волн только 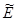2 может распространяться в отраженном луче. В то же время для распространения компоненты Е2¢¢ в пре­ломленном луче препятствий нет. Отсюда сразу можно сде­лать вывод, что и отраженный и преломленный лучи ча­стично поляризованы, причем преимущественное направление в отраженном свете перпендикулярно плоскости падения (Е1) , а в преломленном — лежит в этой плоскости (Е2). На рис.7 рассмотрен случай, когда угол между отраженным и преломленным лучами равен p/2. В этом случае вектор Е2 совпадает с нап­равлением отраженного луча и, следовательно, не может в этом направлении распространяться. Поэтому от­раженный луч полностью линейно поляризован. Поляри­зация преломленного луча при этом максимальная, но далеко не полная (для обычного стекла около 15%). Угол a0 в этом случае называют углом Брюстера или углом пол­ной поляризации. Так как a0+j0=90°, то sin j0= сos a0 , и, учитывая формулу (5), получаем условие

tg a0=n21. (6)

Это условие носит название закона Брюстера. Таким образом, если угол падения светового луча на границу раздела двух диэлектриков удовлетворяет условию (6), то отраженный луч света будет линейно поляризован. Для обычного стекла угол Брюстера составляет около 57°. Измерение угла пол­ной поляризации света при отражении может служить простым методом определения показателя преломления вещества.

Поляризация света при преломлении в изотропных диэлектриках.

Как уже было сказано, поляризация преломленных лучей (даже при падении света под углом Брюстера) да­леко не полная. Для увеличения степени поляризации преломленного света используют стопу стеклянных пластинок (стопа Столетова), располагая их так, чтобы свет падал под углом Брюстера. Достаточно 8—10 наложенных друг на друга стеклянных пластинок, чтобы при падении света под углом Брюстера не только отраженный, но и прелом­ленный свет стал практически полностью поляризованным т.к. отражение на каждой пластине уменьшает в преломленном свете относительную интенсивность колебаний, перпендикулярных плоскости падения. Стопа может служить поляризатором (или анализатором) как в отраженном, так и в проходящем свете.

Для разных областей спектра применяются стопы из разных материалов. Для видимой области практичнее все­го различные сорта стекла, для ультрафиолетовой — плав­леный кварц, для инфракрасной — хлористое серебро, селен.

Поляризация при двойном лучепреломлении.

Гюйгенс создал тео­рию прохождения световой волны через кристалл, объясняющую возникновение двойного лучепреломления. Примененный им ме­тод дает способ определения направления распространения обыкновенного и необыкновенного лучей.

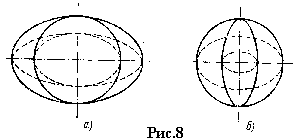
Его теория базируется на предположении о наличии у вол­ны в кристалле двух волновых поверхностей. Скорость обыкно­венной волны v0=c/n0 одинакова во всех направлениях — ей должна соответствовать сферическая волновая поверхность. Скорость необыкновенной волны ve=c/ne зависит от направле­ния ее распространения. Она совпадает по величине с v0 в на­правлении оптической оси кристалла и больше всего отличается от v0 в направлении, перпендикулярном оптической оси. Волно­вая поверхность необыкновенной волны для одноосного кри­сталла имеет вид эллипсоида вращения, который в направлении оптической оси должен касаться сферической волновой поверх­ности обыкновенной волны. Для отрицательного кристалла n0 ³ ne, следовательно, ve ³ v0, т.е. шар вписан в эллипсоид вращения. Для положительного кристалла v0 ³ ve и волновая поверхность обыкновенной волны (шар) охватывает волновую поверхность необыкновенной волны (эллипсоид вращения). На рис. 8 а, б. представлены оба этих случая.

Рассмотрим объяснение двойного лучепреломления по Гюй­генсу. Гюйгенс постулировал, что каждая точка, до которой дохо­дит световое возбуждение, может рассматриваться как центр соответствующих вторичных волн. Для определения волнового фронта распространяющейся волны в последующие моменты времени следует построить огибающую этих вторичных волн.

В случае перехода света из одной изотропной среды в дру­гую построение Гюйгенса предельно просто (рис.9 а): строится плоский фронт падающей волны (ОА) в тот момент времени, когда часть его в точке О дошла до границы раздела. Далее из точки О радиусом ОС=v2Dt (где Dt—время, которое должна была затратить волна, чтобы пройти путь АВ в первой среде) проводится полусфера во второй среде. Очевидно, что АВ ==v1Dt и ОС= 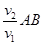. Ту же операцию можно повторить для точек О', О" и т. д. Огибающей всех этих полусфер служит пря­мая ВD, перпендикуляр к которой (луч) составляет угол j2 с нормалью к границе раздела (угол преломления).

Такую же методику построения волнового фронта можно применить для описания перехода волны из изотропной среды в анизотропную. Если для исследуемого кристалла известно на­правление оптической оси, то построение в нем двух волновых поверхностей (обыкновенной и необыкновенной) не представит труда. На рис. 9.б) выполнено такое построение для волны, падаю­щей под некоторым углом j на плоскую поверхность отрицатель­ного кристалла, вырезанного так, чтобы его оптическая ось была параллельна границе раздела.

Касательные к волновым поверхностям определят волновые фронты обыкновенной и необыкновенной волн. Направление потока энергии для обеих волн показано на рис.9,б (лучи о и е). Таким образом, принцип Гюйгенса позволяет определить направления распространения обыкновенного и необыкновенного лучей.

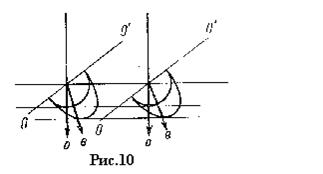
Приведем еще одно построение для случая нормального па­дения световой волны на естественную грань кристалла исланд­ского шпата (рис.10) двойное лучепреломление имеется и в этом случае.

Двумя приведенными примерами можно ограничиться для иллюстрации столь простого и удобного метода построения вол­нового фронта и определения направлений обыкновенного и не­обыкновенного лучей. При построении Гюйгенса наглядно выяв­ляется несовпадение необыкновенного луча с нормалью к вол­новому фронту в кристалле.

Поглощение света в дихроических пластинах.

У некоторых двоякопреломляющих кристаллов (например, турма­лина) коэффициенты поглощения света для двух взаимно перпендику­лярных поляризованных лучей отличаются настолько сильно, что уже при небольшой толщине кристалла один из лучей гасится практически полностью и из кристалла выходит линейно поляризованный пучок света. Это явление называется дихроизмом. В настоящее время дихроические пластинки изготовляют в виде тонких пленок - полярои­дов, имеющих широкое применение. В большинстве случаев они состо­ят из множества маленьких (толщиной до 0,3 мм) параллельно ориен­тированных кристаллов сернокислого йодистого хинина - герапатита, находящихся внутри связующей среды - прозрачной пленки.

Закон Малюса.

Рассмотрим более подробно вопрос об интенсивности линейно поляризованного света, прошедшего через произвольную кристаллическую пластинку. Обозначим через РР направление колебаний вектора Е линейно поляризованного света, вышедшего из пластинки (рис.11).

Для анализа степени поляризации света применяются устройства, называемые анализаторами, в качестве которых используют те же самые поляризаторы (диэлектрики, призмы Николя, поляроиды). Если взять два поляроида (рис. 206, а): один поляроид Р—поляризатор; из него выходит линейно поляризованный свет (вектор Е ко­леблется по направлению РР), второй поляроид А — ана­лизатор (колебания Е по ЛЛ), то по закону Малюса интенсив­ность света I, выходящего из анализатора, пропорциональна квадрату косинуса угла a между направлением плоскостей колебаний (вектора Е) поляризатора и анализатора, т. е.

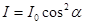(7)

где I0— интенсивность света, выходящего из поляризатора Р, если I0¢ -интенсивность естественного света, то

I0= I0¢/2 (8)

Закон Малюса очень легко выводится. Интенсивности

I0 = 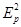, а I = 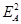, (9)

Ер и ЕА— амплитуды колебаний, прошедших анализа­тор и поляризатор. Из рисунка 11 видно, что

Еа == Ер • cos a (10)

Подставляя выражение (10) в (9), получим:

I = 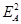= (Ер • cos a)2 == cos 2a.= I0 cos 2a

Если направления плоскостей колебаний поляризатора и анализатора перпендикулярны, т.е. a= 90°, то говорят, что поляризатор и анализатор скрещены (установлены на гаше­ние света — через скрещенные поляризаторы свет не про­ходит).

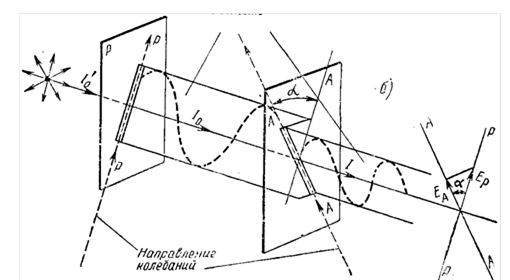
Рис.11

Если направления плоскостей поляризатора РР и анализатора АА совпадают (a =0), то интенсивность про­ходящего света будет максимальной. Для любого другого угла a интенсивность света вычисляется по формуле (7).

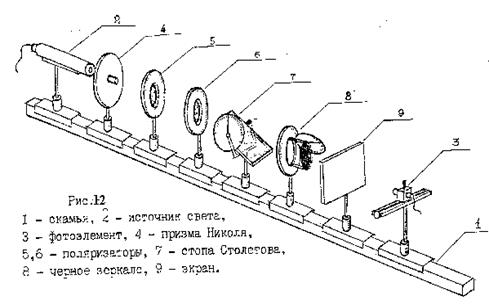
ОПИСАНИЕ УСТАНОВКИ

Установка собирается на оптической скамье 1 (рис.12). Все де­тали должны быть закреплены в рейтерах, позволяющих перемещать их вдоль оптической скамьи. Для получения светового пучка исполь­зуется источник света 2. Интенсивность его определяется с помощью приемника света 3. Линейно поляризованный свет получают с помощью набора поляризаторов: призмы Николя 4, поляризаторов 5 и б, стопы Столетова 7 и черного зеркала 8. Поляроиды и николь могут вращать­ся вокруг горизонтальной оси и для отсчета углов поворота снабже­ны вертикальными лимбами.

Стопа Столетова 7 закреплена в оправе с вертикальным лимбом, позволяющим поворачивать ее вокруг горизонтальной оси. Черное зер­кало может вращаться как вокруг вертикальной, так и вокруг горизон­тальной осей. Отсчет углов поворота при этом производится соответ­ственно по горизонтальному и вертикальному лимбам. Экран 9 служит для получения изображения источника света.

Питание источника света осуществляется блоком питания 10 (БП-1).

Приемник света 3 преобразует световой поток в электрический ток, величина которого прямо пропорциональна интенсивности падающего на приемник света и измеряется с помощью микроамперметра II.

ВЫПОЛНЕНИЕ РАБОТЫ

Упражнение 1.. Определение направления колебаний вектора Е в поляризованном свете и показателя преломления материала.

1. Установить на оптическую скамью источник света, поляроид и черное зеркало. Экран снять с оптической скамьи и расположить у стенки лабораторного стола таким образом, чтобы при проведении опыта свет, отраженный от черного зеркала падал на экран.

2. Включить блок питания источника. Установить интенсивность светового потока, соответствующую среднему положению ручки регу­лировки выходной мощности блока питания.

3. Найти положение зеркала, при котором световой луч падал бы на него под углом Брюстера. Для этого, вращая поляроид вокруг направления луча, а зеркало вокруг вертикальной оси, добиться прак­тически полного исчезновения светового пятна на экране. По гори­зонтальному лимбу на оправе зеркала измерить угол падения луча a0. Положение поляроида и зеркала уточнить несколько раз, так чтобы система поляроид-зеркало не пропускала свет. В этом случае зеркало установлено под углом Брюстера, а в падаю­щей на него световой волне колебания вектора Е совершаются в пло­скости падения. Найти среднее значение угла Брюстера.

4. По среднему значению угла Брюстера, используя формулу (6), вычислить показатель преломления молибденового стекла, из которо­го сделано зеркало.

Упражнение 2. Изучение поляризованного света при помощи анализаторов различного типа.

1. Черное зеркало.

Приборы и их расположение на оптической скамье оставить теми же, что и в упражнении 1. Черное зеркало должно быть расположено в вертикальной плоскости (отсчет по вертикальному лимбу amin=0 или amfx=180°).

1.1. Установить черное зеркало под углом Брюстера. Интенсивность отраженного света при этом должна быть минимальна.

1.2. Не изменяя угла падения луча и следя за изображением от­раженного луча на экране (экран по мере необходимости перемещать, располагая его над зеркалом) вращать черное зеркало вокруг гори­зонтальной оси до положения, в котором интенсивность отраженного света максимальна. Отметить это положение по вертикальному лимбу. Измерения повторить несколько раз. Результаты занести в таблицу.

1.3. Дать схему хода лучей при максимальной интенсивности от­раженного света.

2. Стопа Столетова.

2.1. Заменить черное зеркало стопой пластин. Повторить опе­рации, выполненные с черным зеркалом; наблюдения провести как в от­раженном, так и в проходящем свете. Измерить несколько раз поло­жения стопы, в котором интенсивности максимальны. Результаты для отраженного и для проходящего света занести в таблицу.

2.2. Дать схему хода лучей для двух положений стопы: когда интенсивность отраженного света максимальна и когда она минимальна. При этом показать направление колебаний вектора Е на различных участках луча.

3. Николь.

3.1. Заменить стопу пластин николем. Повернуть его до положе­ния, при котором интенсивность пропускаемого света будет максималь­ной. При этом следует пройти дальше максимума и, заметив ослабление света, вернуться обратно.

3.2. Вращая николь вокруг горизонтальной оси, отметить положение, со­ответствующее максимальной и минимальной интенсивности проходяще­го света в пределах одного оборота анализатора. Результаты занести в таблицу.

3.3. Изобразить полную схему хода луча, отмечая направления колебаний вектора Е на различных участках пути для двух положений николя, соответствующих максимальной и минимальной интенсивности пропущенного света.

Упражнение 3. Проверка закона Малюса.

1. Установить на оптической скамье источник света, два поля­роида и фотоэлемент. Последний должен располагаться примерно в центре светового пучка (проверьте с помощью экрана).

2. Задать минимальную яркость источника, регулируя выходную мощность блока питания.

3. Вращая поляроиды вокруг направления луча, добиться макси­мальной интенсивности пропущенного света. Согласно формуле (7), для этого положения a=0 , 1=1о. Значение a=0 может не совпадать с нулевым делением j =0 лимба поляроида.

4. Включить миллиамперметр и установить переключатель шкалы в положение "х10".

Увеличивая мощность источника добиться максимального отклоне­ния стрелки миллиамперметра.

5. Измерить величину тока, пропорциональную интенсивности пропущенного света, поворачивая один из поляроидов последователь­но на 20° в пределах полного оборота, и занести результаты в таб­лицу. Угол a при этом определяется как разность показателей шка­лы лимба поляроида для данного положения и начального.

б. Построить график экспериментальной зависимости 1/10=f(a) в полярных координатах. Для этого на каждом луче, проведенном из центра 0 под углом a, в выбранном масштабе отложить значения величин 1/10, соответствующих этому углу a. Точки соеди­нить плавкой кривой. На этом же чертеже аналогичным способом пост­роить теоретическую зависимость 1/10= cos 2a.

Контрольные вопросы:

1. Сформулируйте закон Брюстера.

2. Чему равен угол между отраженным и преломленным лучами, когда отраженный луч полностью поляризован?

3. При отражении света от каких веществ можно наблюдать полную поляризацию отраженного луча?

4. Объясните с помощью теории Гюйгенса образование двух лучей при прохождении света через анизотропные кристаллы.

5. Сформулируйте закон Малюса.

6. Каким образом можно получить полностью поляризованный преломленный свет?

7. Как устроена призма Николя?

Лабораторная работа№9

ИЗУЧЕНИЕ ЯВЛЕНИЯ ВРАЩЕНИЯ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ.

Целью работы является изучение явления вращения плоскости поляризации оптически активными веществами и определение неизвестной концентрации раствора.

Приборы и принадлежности: сахариметр, кюветы с растворами сахара.