Решение дифференциальных уравнений линейных стационарных САУ. Свободный и вынужденный режим движения САУ.
Решение дифференциальных уравнений линейных стационарных САУ.
Рассмотрим уравнение (18). Очень часто при описании САУ необходимо определить процесс изменения выходной величины X. При этом параметры системы заданы, следовательно коэффициенты ai, i=1,n, bj, j=0,m известны, входная переменная f(t) также известна, известны начальные условия по X и его производным ( они или задаются или пересчитываются из начальных условий по входным переменным САУ) и необходимо определить характер изменения X(t). Для определения функции X(t) необходимо решить дифференциальное уравнение (18).
Методы решения могут быть аналитическими и численными. Численные методы рассматриваются в соответствующем курсе, а для нас наибольший интерес будут представлять аналитические методы. Мы рассмотрим классический метод вариации произвольных постоянных (метод Лагранжа) и метод, использующий преобразования Лапласа.
Уравнение (18) заменой
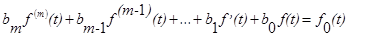
может быть сведено к уравнению
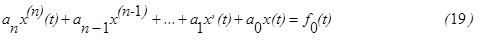
При использовании классического метода решение уравнения (19) находится как сумма общего решения соответствующего однородного уравнения и частного решения неоднородного дифференциального уравнения. Методы поиска этих решений рассмотрены в теории дифференциальных уравнений. Основная сложность состоит в определении фундаментальной системы решений однородного дифференциального уравнения.
Пример
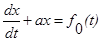
однородное дифференциальное уравнение имеет вид
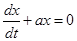
и оно имеет решение
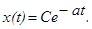
Найдем решение неоднородного уравнения. Полагаем, что
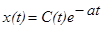
Тогда 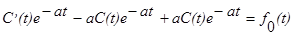 ,
,
Откуда
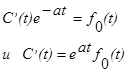
после чего находится функция С(t) и решение неоднородного уравнения.
Классические методы применимы, если в интервале (t0,¥) функция f0(t) и известны начаьлные условия при t0¹0. Однако для многих САУ эти условия не выполняются. Для непрерывности f0(t) в исходном уравнении (18) функция f(t) должна быть m- кратно непрерывно дифференцируема на интервале (t0,¥). Этг условие для многих функций выполняется, но возникают особености при t=t0. Дело в том, что f(t)º0 при t<t0 и часто f(t0+0)¹0 (например, такая ситуация имеет место при f(t)=1(t). При этом правая часть уравнения (18) при t=t0 имеет разрывы второго рода. Вследствие этого при t=t0 имеют разрывы производные функции x(t), так что начальные значения при t=t0+0 должны определяться дополнительно. Однако в курсе МОТАУ было показано, что в этом случае для решения уравнения (18) может использоваться преобразование Лапласа, в которых при вычитании изображений производных используются начальные условия слева, т.е. при t0-0. Это было строго доказано. Проиллюстрируем последовательность действий в этом случае на примере.
Рассмотрим уравнение 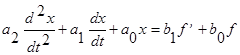 и пусть
и пусть 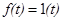 . При этом
. При этом 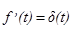 и в момент времени t=0 имеет место скачок
и в момент времени t=0 имеет место скачок 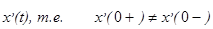 .
.
При формальном использовании преобразований Лапласа имеем 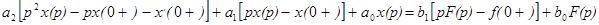
Реально нам известны начальные условия до подачи входного сигнала, т.е. x,(0-), x(0-). Но если x(0+)¹x(0-), то x’(t) при t=0 испытывает скачок, x,(0+)¹x,(0-) и x,(0+) должна специально определяться.
Но можно найти решения, используя преобразования Лапласа с “левыми” начальными условиями: Получим
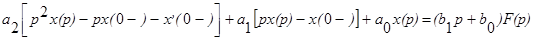
(при этом f(0-)=0 по определению функции f(t)). Далее мы находим решение так же, как обычно, т.е. определим x(p) и вычисляем 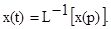
Свободный и вынужденный режим движения САУ.
Рассмотрим процесс решения уравнения (18)
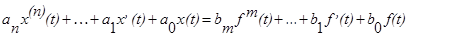
с помощью преобразований Лапласа. Положим
t0=0, f(t)º0 при t<0, начальные условия нулевые, т.е.
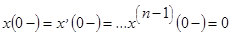
обозначим 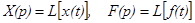 .
.
Применяя преобразования Лапласа к обеим частям уравнения, получим
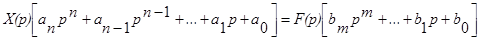
Введем обозначения:
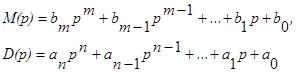
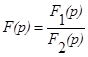 - правильная алгебраическая дробь (эта ситуация имеет место для всех рассматриваемых нами воздействий).
- правильная алгебраическая дробь (эта ситуация имеет место для всех рассматриваемых нами воздействий).
Тогда с учетом введенных обозначений
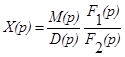 - это выражение представляет собой правильную алгебраическую дробь.
- это выражение представляет собой правильную алгебраическую дробь.
Рассмотрим общий вид решения x(t). Предположим, что многочлены D(p), F2(p) имеют простые различные корни и степень многочлена F2(p) равна r. Тогда, как следует из курса МОТАУ
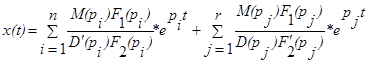 ,
,
где pi, i=1,n – корни уравнения D(p),
pj, j=1,r – корни уравнения F2(p),
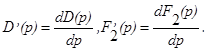
Характер изменения слагаемых первой суммы определяется корнями pi, корнями многочлена D(p), зависящими от параметров системы. Но коэффициенты при 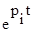 зависят и от вида входного воздействия f(t).
зависят и от вида входного воздействия f(t).
Характер изменения слагаемых второй суммы определяется корнями многочлена F2(p), т.е. он зависит от вида входного сигнала.
Можно записать
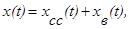
где 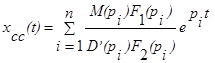 - собственное сопровождающее движение системы,
- собственное сопровождающее движение системы,
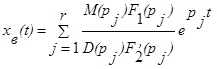 - Вынужденное движение системы.
- Вынужденное движение системы.
Таким образом, вынужденное движение – это движение, возникающее только при наличии входного сигнала. Вид этого движения определяется видом входного сигнала. Например, если f(t)ºt, то общий вид вынужденного движения будет 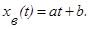
Если 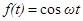 , то
, то 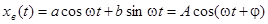 и т.д.
и т.д.
Собственное сопровождающее движение также возникает при наличии входного сигнала, но его характер определяется свойствами самой системы(корнями полинома D(p)).
Рассмотрим теперь решение дифференциального уравнения (18) с учетом начальных условий 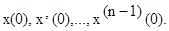 С учетом теоремы об изображении производной, имеем
С учетом теоремы об изображении производной, имеем
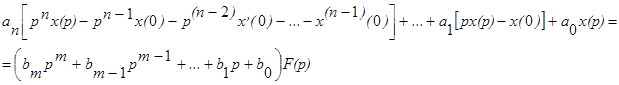
(начальные условия по входному сигналу полагаем нулевыми), или
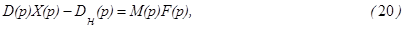
где 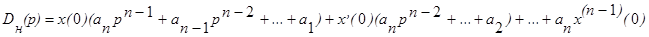 - многочлен, зависящий от коэффициентов a1,a2,..,an и начальных условий.
- многочлен, зависящий от коэффициентов a1,a2,..,an и начальных условий.
Из (20) найдем
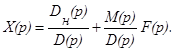
Обратное преобразование второго слагаемого уже было рассмотрено. При обратном преобразовании первого слагаемого получим
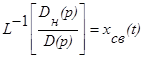
- свободное движение системы- это движение, возникающее в отсутствии входного сигнала и определяемое наличием не нулевых начальных условий.
Для случая простых корней D(p)
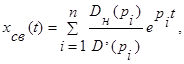
т.е. его характер совпадает с характером собственных сопровождающих движений.
Таким образом, общее решение x(t) можно представить в виде
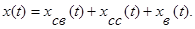
Сумму 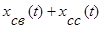 назовем собственным движением системы.
назовем собственным движением системы.
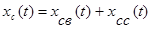
и
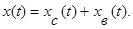
Если 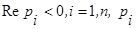 - корни многочлена D(p), то
- корни многочлена D(p), то
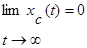
и тогда
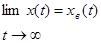
Процесс 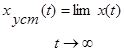 назовем установившимся режимом работы САУ. В данном случае
назовем установившимся режимом работы САУ. В данном случае 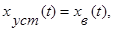 обычно так и бывает.
обычно так и бывает.
Процесс перехода САУ из одного режима в другой назовем переходным режимом. В формировании переходного режима участвуют как собственные, так и вынужденные движения.
Пример.
Пример. Пусть уравнение, описывающее поведение САУ, имеет вид
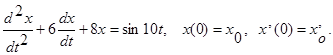
Решаем его с помощью преобразований Лапласа:
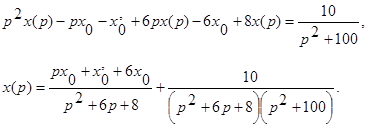
В данном случае
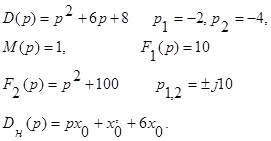
Из сказанного ранее следует, что
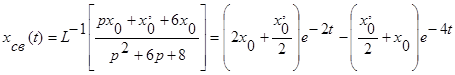
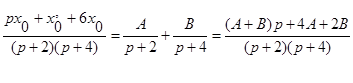
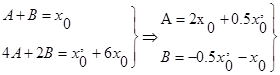
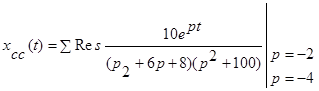
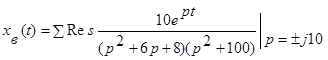
Но xсс(t) и xв(t) можно найти с помощью разложения изображения на простейшие дроби. Имеем:
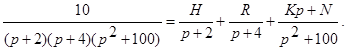
Определяя H,R,K,N методом неопределенных коэффициентов, найдем
H=0.0048, R=-0.043, K=-0.005, N=-0.076
и тогда
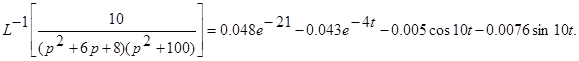
Здесь 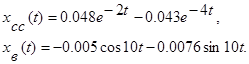
Общее решение имеет вид
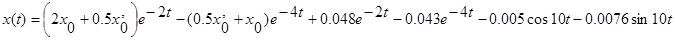
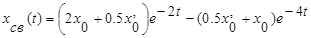
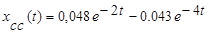
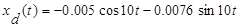
При 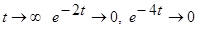 и в системе устанавливается движение
и в системе устанавливается движение
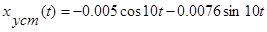
| <== предыдущая лекция | | | следующая лекция ==> |
| Способы математических описаний САУ. | | | Передаточная функция. Структурный анализ непрерывных линейных САУ. |
Дата добавления: 2017-10-04; просмотров: 2390;











