Способы математических описаний САУ.

При составлении математических описаний САУ используют три основных способа. Это:

1.Поэлементный в физических переменных вход-выход на базе физических законов, действующих в простейших частях системы.

2.С помощью уравнений, разрешенных относительно выходных переменных системы (управляемых величин).

3.С помощью уравнений состояния системы.

Третий способ мы пока оставим в стороне и сосредоточимся на первых двух.

1.При первом способе уравнения САУ представляют собой совокупность входящих в систему элементов. Эти элементы могут иметь различную физическую природу (механические, электромеханические, пневматические и т.д.). Для составления их уравнений используются законы Ньютона, Кирхгоффа, Ома и т.д. Методика составления уравнений разработана в таких дисциплинах, как механика, гидравлика, электромеханика.

Пример поэлементного описания САУ.

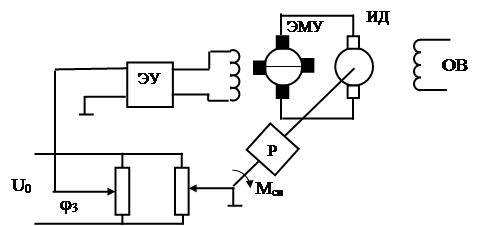Рассмотрим пример поэлементного описания системы на постоянном токе. Принципиальная схема системы приведена на рисунке 29.

Рис.29

ЭУ - электронный усилитель

ЭМУ – электромашинный усилитель

ИД – исполнительный двигатель

a_вх, М_с – входные переменные (задающее воздействие и нагрузка)

a_вых – выходная переменная (управляемая величина)

В данной САУ можно выделить: блок потенциометров, ЭУ, ЭМУ, исполнительный двигатель с редуктором и объектом управления.

1.Блок потенциометров:

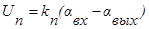, k- коэффициент передачи потенциометра.

2.ЭУ:

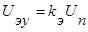
3.ЭМУ – это 2 генератора, соединенных последовательно:

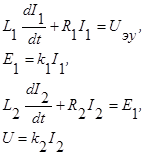
Здесь U_эу – входная переменная ЭМУ, U – выходная переменная, I₁,I₂,E₁ – промежуточные переменные. Исключая их, получаем уравнение ЭМУ, содержащее только входную и выходную переменные:

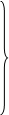
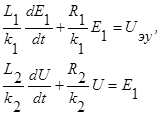
Исключены I₁,I₂, осталось исключить E_1.

Продифференцируем второе уравнение и проведем последовательные преобразования:

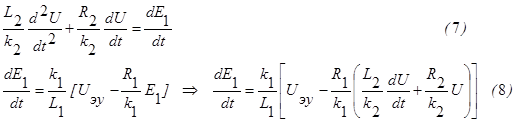
Подставляя (8) в (7), получим:

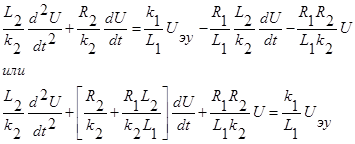
Обычно в ТАУ уравнение приводят к виду, когда коэфф. при U равен 1, т.е.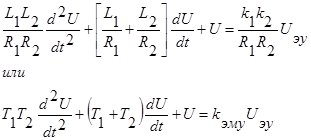

где 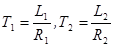- постоянные времени, характеризующие нарастание токов в обмотке ЭМУ, k_эму – коэффициент передачи ЭМУ. Обычно T_1*T₂<<T₁+T₂ ЭМУ приближенно описывается дифференциальным уравнением:

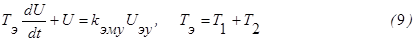
4.Исполнительный двигатель с редуктором. Входная величина – U, выходная – угол поворота вала двигателя a.

Уравнение ЭДС в цепи якоря двигателя:

где 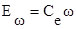- противоэдс, возникающая при вращении якоря;

Уравнение моментов

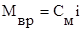- вращающий момент электродвигателя.

I – основной момент инерции двигателя и ОУ, приведенный к двигателю.

M_с – момент сопротивления, приведенный к двигателю.

Здесь нужно исключить переменные i и w. Покажем, как это делается с помощью преобразований Лапласа. Перейдем от (10)-(12) к уравнениям в изображениях. Тогда

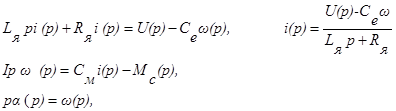
откуда

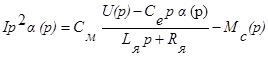
или

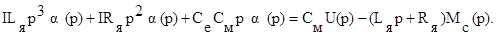
Приводя уравнение к стандартному для ТАУ виду и переходя к оригиналам, получим

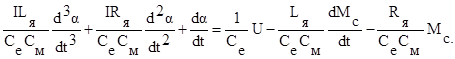
Будем считать, что L_я » 0. Это педположение позволяет упростить уравнение двигателя:

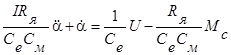
или

где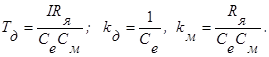

Редуктор – это безинерционное звено:

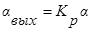
Таким образом САУ дает следующую систему уравнений:

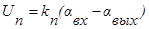
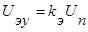
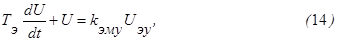
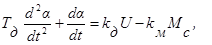
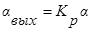
В общем случае систему дифференциальных уравнений, получающуюся в результате поэлементного описания можно представить в следующей матричной операторной форме:

где 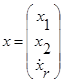- матрица выходных переменных элементов,

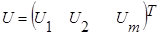- матрица входных переменных системы, N(p) – неособая квадратная (r*r) полиномная матрица, 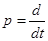- оператор дифференцирования.

В нашем случае , ,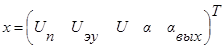

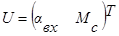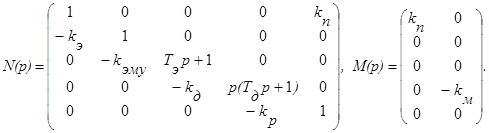
Математическое описание САУ с помощью уравнений, разрешаемых относительно выходных переменных.

Уравнения САУ в форме (14) или (15) удобны для первоначального составления математического описания по исходным физическим данным, но они не удобны для исследования. В них входят промежуточные “лишние” переменные, что делает матрицы N(p) и M(p) более громоздкими. Поэтому форма (15) является промежуточной для перехода к более удобным формам.

Переход к уравнению, содержащему только одну переменную X_i, (например X₁) проводится исключением остальных переменных. Это исключение может быть выполнено традиционными способами теории дифференциальных уравнений, но наиболее удобно выполняется с использованием записи уравнений в операторной форме (15).

Для этого переменные X_i, i=1,r рассматриваем как неизвестные, входные переменные U_j, j=1,m – как известные переменные, полиномы N_ij(p),M_ij(p) – как функции комплексного переменного. Система (15) рассматривается как система уравнений с r неизвестными, которая разрешается относительно интересующих нас переменных, т.е.

где D_i(p) – полином, X_i – скалярная переменная, Mⁱ(p) – матрица-строка.

Уравнение (16)можно получить непосредственно используя способ Крамера. При этом полиномы D_i(p) будут одинаковы для всех i,

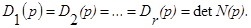
В рассмотренном примере получим уравнение для переменной a_вых. Тогда

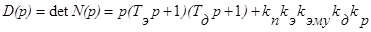
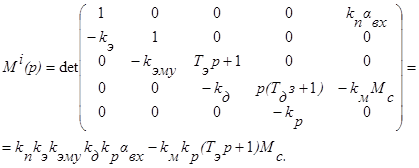
Обозначим К= 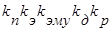. Тогда уравнение (16) для данной САУ примет вид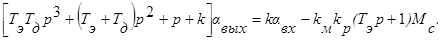

Это уравнение для выходной величины a_вых, записанное в операторной форме. В своей обычной форме оно имеет вид: 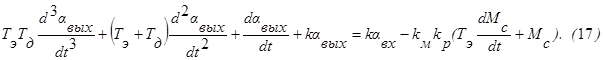Уравнение (17) представляет собой уравнение следящей системы, разрешенное относительно выходной переменной a_вых. Аналогичные уравнения могут быть получены и для величин U_п,U_эу,U,w,a.

Отметим, что при переходе от системы уравнений (15) к уравнению (16), в принципе могут быть получены эквивалентные математические описания и нужно следить, чтобы этого не произошло.

Прежде всего при решении (15) если det N(p) и элементы Mⁱ(p) для некоторого i имеют общий множитель, то его обычно сокращают и получают уравнение (16), в котором степень D_i(p) меньше степени det N(p). Эта операция неверна: при этом не всякое решение (15) будет решением уравнения (16).

Покажем, как это может произойти. Исходная система имеет вид:

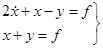
Решаем ее обычным способом:

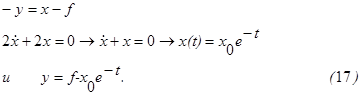
Пусть, например, f=1, x₀=1. Тогда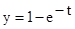

Запишем, что при f=1, x=0 y=1.

С другой стороны, применяя способ Крамера, получим:

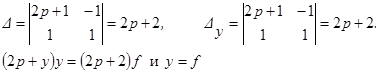
Это, безусловно, решение исходного уравнения, но только одно решение из множества, определяемое выражением (17).

Запишем также, что при переходе от поэлементного САУ к уравнениям высокого порядка относительно выходных переменных (или любой другой интересующей нас переменной) необходимо согласовывать начальные условия по тем переменным, которые участвуют в этих описаниях. В противном случае решения системы (15) и уравнения (16) могут не совпадать.

В общем случае дифференциальное уравнение, определяющее изменение выходного сигнала САУ x(t) при некотором входном воздействии f(t) (задающем или возмущающем) имеет следующий вид:

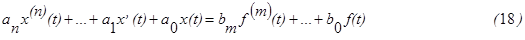
Именно такие уравнения мы будем рассматривать в дальнейшем. Учет возможного наличия нескольких входных сигналов может проводиться непосредственно в правой части уравнения (18) или с помощью принципа суперпозиции.