Дифференциальные зависимости между крутящим моментом и интенсивностью крутящего момента.
Помимо внешних сосредоточенных крутящих моментов на стержень (вал) может действовать распределенная по некоторому закону моментная нагрузка интенсивностью 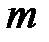 (
( 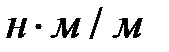 ). Между этой внешней моментной нагрузкой
). Между этой внешней моментной нагрузкой 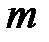 и крутящим моментом
и крутящим моментом 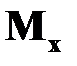 существует дифференциальная зависимость.
существует дифференциальная зависимость.
Рассмотрим стержень, загруженный распределенной моментной нагрузкой рис.16.8а.
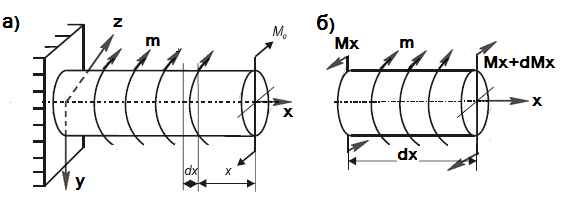
Рис. 16.8 К выводу дифференциальной зависимости между 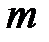 и
и 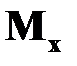
Вырежем из скручиваемого стержня на участке, где действует 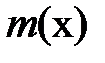 элемент
элемент 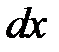 и рассмотрим его равновесие (рис.16.8,б). Влияние отброшенных частей заменим действием крутящих моментов
и рассмотрим его равновесие (рис.16.8,б). Влияние отброшенных частей заменим действием крутящих моментов 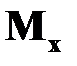 и
и 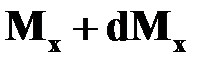 . Вследствие малости
. Вследствие малости 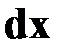 распределенную вдоль элемента нагрузку можно считать постоянной. Составим уравнение равновесия элемента:
распределенную вдоль элемента нагрузку можно считать постоянной. Составим уравнение равновесия элемента:
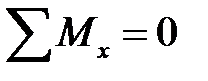 ,
, 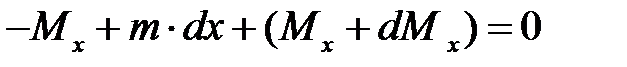 ,
,
где произведение 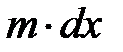 представляет собой равнодействующую скручивающей нагрузки на участке
представляет собой равнодействующую скручивающей нагрузки на участке 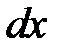 . Поделив это уравнение на
. Поделив это уравнение на 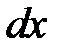 получим искомое дифференциальное соотношение
получим искомое дифференциальное соотношение
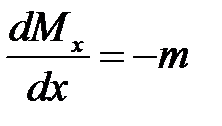 . .
| (16.12) |
С учетом формулы (16.5) 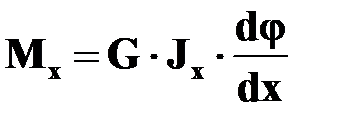 получим
получим
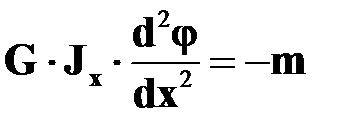
| (16.13) |
Пример 16.1 Построить эпюры 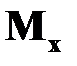 и
и 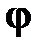 для стержня ступенчато постоянного сечения, представленного на рис.16.9.
для стержня ступенчато постоянного сечения, представленного на рис.16.9.
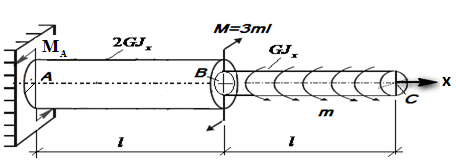
Рис. 16.9 Расчетная схема стержня
Жесткость участка ВС обозначим через 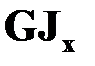 . На этом участке действует равномерно распределенная скручивающая нагрузка с интенсивностью
. На этом участке действует равномерно распределенная скручивающая нагрузка с интенсивностью 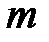 . Жесткость участка АB равна
. Жесткость участка АB равна 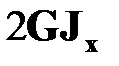 . В сечении
. В сечении 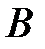 действует сосредоточенный момент
действует сосредоточенный момент 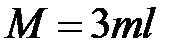 .
.
Определим крутящий момент в защемлении 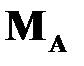 (внешняя сила) (рис16.9)
(внешняя сила) (рис16.9)
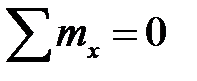 ,
, 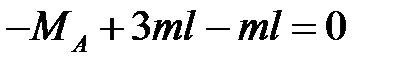 ,
, 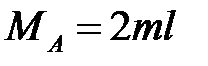 .
.
Проведем сечение в произвольном месте 1-го участка
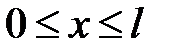
 Рис. 16.10 Участок AB
Рис. 16.10 Участок AB
| 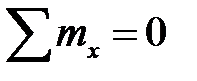 , , 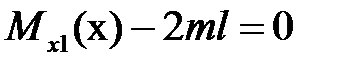 , ,
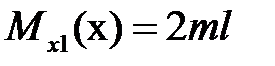 , , 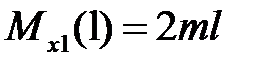
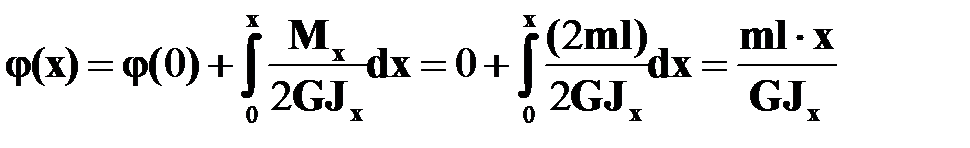  , , 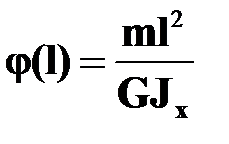
|
Проведем сечение в произвольном месте 2-го участка
( 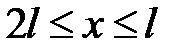 ) ) 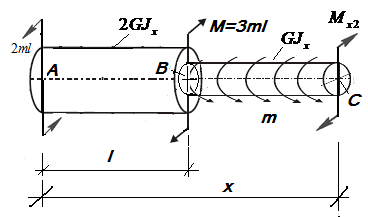 Рис. 16.11Участок BC Рис. 16.11Участок BC
|  , ,
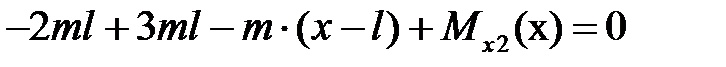
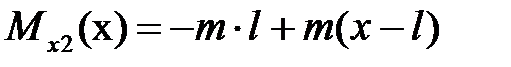 . .
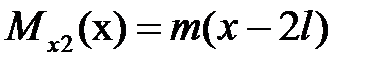
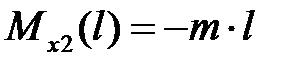 , , 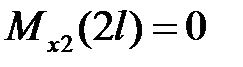 . .
|
Для угла закручивания 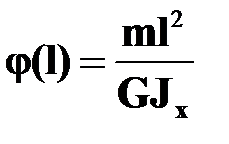 . Согласно (16.9)
. Согласно (16.9) 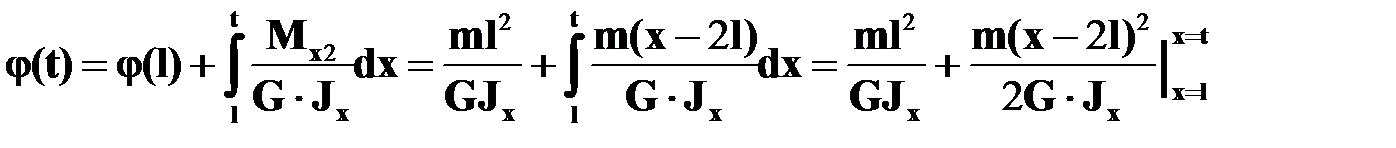 .
.
Значения 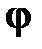 на участке :
на участке : 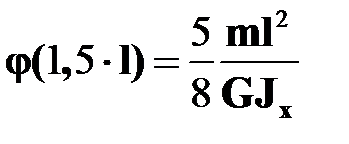 ,
, 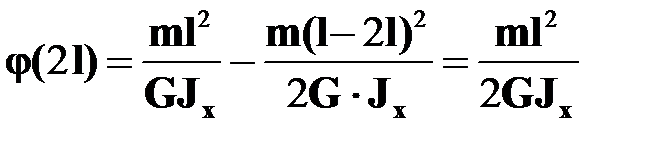 .
.
Строим эпюры (рис.16.12)
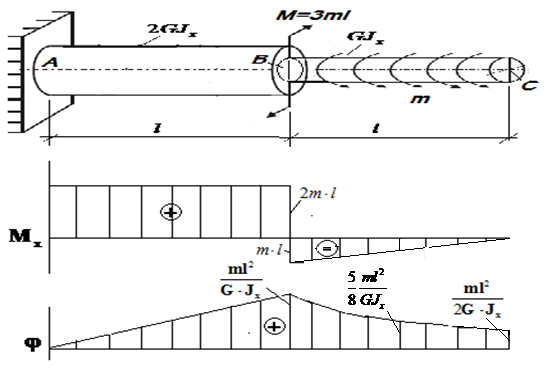
Рис.16.12 Эпюры крутящих моментов  и углов закручивания
и углов закручивания 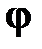
Дата добавления: 2017-09-01; просмотров: 2068;











