Анализ точности и качества линейных систем автоматического регулирования.

План лекции:

Критерии качества САУ.

Качество работы любой системы, в конечном счете, определяется величиной ошибки, равной разности между требуемым и имеющимся значением регулируемой величины

.

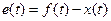Качество работы системы оценивают по некоторым ее свойствам, проявляющимся в так называемых типовых режимах. Для определения качественных показателей САУ используются так называемые критерии качества.

Известно большое число критериев качества. Все их можно разбить на несколько групп.

К первой группе можно отнести критерии, определяющие запасы устойчивости. Эти критерии уже рассматривались ранее и здесь мы их затрагивать не будем.

Ко второй группе относятся критерии, использующие для оценки качества величину ошибки в различных типовых режимах. Их можно назвать критериями точности системы автоматического регулирования.

К третьей группе можно отнести критерии, характеризующие протекание переходных процессов в системе. Это, в частности, время регулирования и перерегулирования САУ.

И, наконец, могут использоваться комплексные критерии, характеризующие некоторые обобщенные свойства системы. Они могут одновременно учитывать, в той или иной степени, точность, запасы устойчивости, быстродействие системы. Обычно они представляют собой некоторые интегральные показатели процесса регулирования.

Вынужденные процессы и точность САУ в типовых режимах.

В общем случае на систему действует управляющее и возмущающее воздействия. Используя принципы суперпозиции, можно рассматривать поведение системы при каждом из них, объединяя в дальнейшем полученные результаты.

Рис.80

Ступенчатый входной сигнал.

1.Рассмотрим поведение замкнутой системы, структурная схема которой показана на рис.80 при подаче на ее вход ступенчатого сигнала .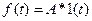

Пусть 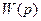передаточная функция разомкнутой статической системы

,

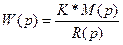здесь К – коэффициент передачи разомкнутой САУ, M(p), R(p) – многочлены такие, что M(0)=1, R(0)=1. Тогда

,

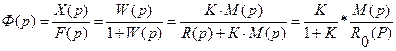где R₀(p) – многочлен от p и R₀(0)=1. Положим для простоты, что корни 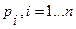многочлена R₀(p) – действительные простые и

.

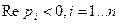Найдем реакцию системы на ступенчатый входной сигнал при нулевых начальных условиях. Обозначим

.

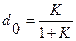Тогда

и

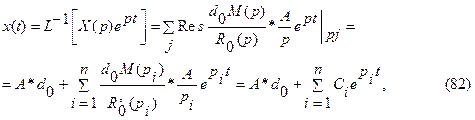
где 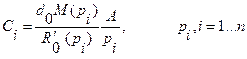- корни многочлена R₀(p).

В (82) первое слагаемое 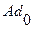соответствует вычету в полюсе изображения F(p) входного сигнала p=0. Оно определяет вынужденный процесс таким образом

Сумма 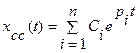- это собственное сопровождающее движение. В устойчивой замкнутой системе

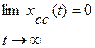
и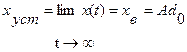

Из приведенного рассмотрения следует результат:

при постоянном входном сигнале вынужденный процесс также постоянная величина.

Общий случай.

2.Рассмотрим общий случай. Пусть W(p) имеет астатизм порядка r, т.е
,

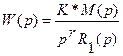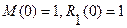. Тогда

(*)

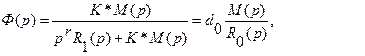где 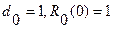. Таким образом, передаточная функция замкнутой САУ всегда сводится к виду (*). Для статической системы 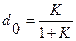, для астатической .

Пусть входной сигнал имеет вид

.

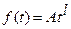Тогда

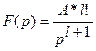
и

Как и раньше посчитаем, что многочлен R₀(p) имеет простые действительные корни.

Для определения процесса в системе разложим изображение X(p) на сумму простых дробей. Получим

.

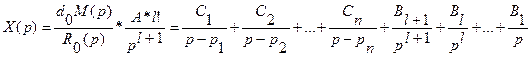В полученном разложении сумма

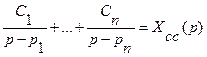
определяется полюсами передаточной функции Ф(p) и соответствует собственному сопровождающему движению, а сумма

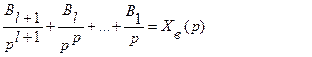
определяется полюсами изображения входного сигнала F(p) и соответствует вынужденному движению. При этом с учетом () будем иметь

.

Таким образом, получен следующий результат. Вынужденный процесс в САУ при полиномиальном входном воздействии представляет собой полином той же степени, что и входной сигнал. Коэффициенты этого полинома зависят от параметров системы и коэффициентов входного сигнала.