Выделение областей устойчивости.

Выделение области устойчивости на плоскости одного параметра.

Пусть нас интересует влияние на устойчивость параметра α, линейно входящего в характеристическое уравнение (77). При этом уравнение (77) можно представить в виде

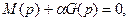(79)

где M(p), G(p) – некоторые полиномы.

Чтобы построить области с одинаковым количеством левых корней относительно параметра α необходимо в (77) выполнить подстановку p=jw и задаваясь ω: - ∞<ω<+∞ , построить на плоскости α график

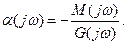
В дальнейшем этот график будем называть Д – кривой.

Представив α=x+jy, получим

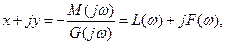
где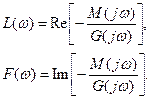

Так как L(ω) – четная функция, F(ω) – нечетная функция, то Д – кривая на плоскости Д симметрична относительно оси абсцисс. Поэтому можно построить ветвь, соответствующую 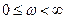и дополнить ее симметричной относительно действительной оси.

Пусть Д-кривая построена и имеет вид, представленный на рисунке 74.

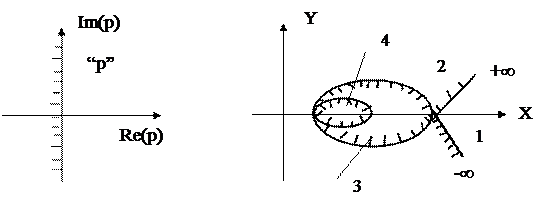Рис.74.

В данном случае плоскость Д разбита на 4 области равных количеств левых корней. Возникает вопрос: сколько именно левых корней соответствует каждой области и какая из областей является областью устойчивости.

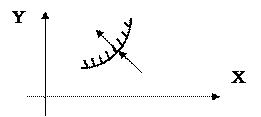Для выявления области устойчивости заштрихуем левые стороны мнимой оси плоскости “p” и Д-кривой плоскости Д при движении по ней, соответствующем изменению ω от -¥ до +¥. После выполнения штриховки не трудно выделить область устойчивости. Для этого нужно учесть, что переходу из одной области плоскости Д в другую, показанному на рисунке 75,

Рис.75.

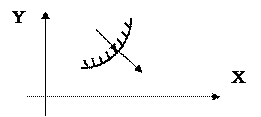соответствует переход корня “p” из правой полуплоскости в левую. При переходе на плоскости Д, показанном на рисунке 76, на плоскости “p”

Рис.76.

происходит переход корня из левой полуплоскости в правую. Таким образом, если обозначить область 1 как Д_к, область 2 будет областью Д_к+1, 3-Д_к+2 и 4-Д_к+3. Областью устойчивости может быть только область 4, если к+3=n, где n - порядок системы. Так ли это проверяется непосредственным применением какого-либо критерия устойчивости к характеристическому уравнению (79), в котором значение параметра a взято из области 4.

Пример. Выполним Д-разбиение по коэффициенту передачи разомкнутой системы, структурная схема которой показана на рис.77.

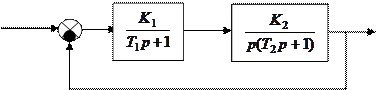Рис.77

Передаточная функция разомкнутой системы имеет вид

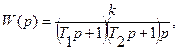
где 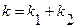. Характеристическое уравнение имеет вид

.

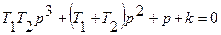Выполнив подстановку 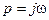и полагая 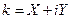, получим соотношения

,

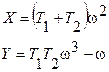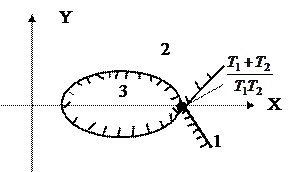задающие Д-кривую на плоскости Д. Задаваясь значением w:-¥<w<+¥, построим эту кривую (см. рис. 78).

Рис.78.

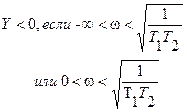
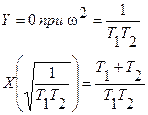
Эта кривая выделяет на плоскости Д 3 области. Областью устойчивости может быть только область 3, она ей и является – это можно непосредственно проверить. Таким образом, области 3 соответствует 3 левых корня характеристического уравнения, области 2 – 2 таких корня и области 1 – 1 такой корень. При 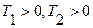ситуация, когда все корни характеристического уравнения расположены в правой полуплоскости плоскости “p” невозможна – такой области нет в области Д-разбиения, это легко показать и непосредственным анализом характеристического уравнения.

Выделение области устойчивости на плоскости 2 параметров.

Предположим, что имеются 2 параметра a и b, влияние которых на устойчивость требуется оценить. Будем считать, что эти параметры входят в характеристическое уравнение

линейно.

Подставляя в (80) 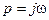, получим

,

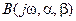откуда

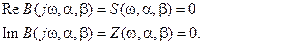(81)

Зависимости (81) задают Д-кривую на плоскости (a,b). Штриховка на плоскости 2 параметров производится по следующему правилу. Перемещаясь вдоль Д-кривой в сторону увеличения w нужно штриховать ее с левой стороны, если определитель

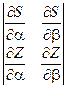
положителен и справа, если этот определитель отрицателен. Дальнейшие рассуждения остаются такими же, что и для случая Д-разбиения по одному параметру.

Пример. Рассмотрим ту же следящую систему, что и в предыдущем примере и выполним для нее построение области устойчивости на плоскости двух параметров: коэффициента передачи К и постоянной времени T₁. Имеем

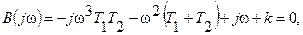
откуда

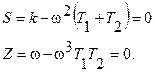
Решая это уравнение относительно k,T₁, имеем

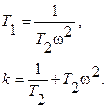
Задаваясь различными значениями w, строим Д-кривую (см. рис.79 )

Рис.79

Определим направление штриховки. Имеем

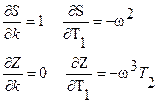
Определитель равен

.

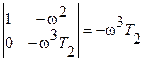При движении по Д-кривой снизу вверх (w<0) определитель положителен, штриховка наносится слева по ходу движения, при движении по Д-кривой сверху вниз (w>0) определитель отрицателен и штриховка наносится справа. Таким образом снизу от кривой получается двойная штриховка.

Область устойчивости определяется двумя координатными положительными полуосями и полученной Д-кривой.