Вопрос 2. Взаимодействие света с веществом.

Прежде чем ознакомиться с устройством и принципом действия лазера, рассмотрим некоторые вопросы взаимодействия света с веществом.

Прохождение света через среду приводит к ослаблению интенсивности светового потока в соответствии с законом Бугера

(см. также выражение (11.10)):

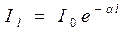,(24.16)

где α — линейный коэффициент погло­щения света веществом; I_l – интенсивность света, вышедшего из слоя вещества толщиной l.

В классической линейной оптике всегда α > 0 и, следовательно, всегда наблюдается поглощение света.

Зависимость I от толщины слоя х при α > 0, согласно формуле (24.16), приведена на рис. 24.2. Там же дана аналогичная зависимость при α = 0 и α <0. Из этой зависимости вытекает весьма любопытный факт: для

α < 0 при прохождении светового потока через среду происходило бы его усиление, т. е. по­глощение было бы отрицательным. Существует ли отрицательное поглощение в реальных средах? Оказывается, реализовать такое поглощение можно.

Отрицательное поглощение. В 1939г.

впервые А. Фабрикантомбыла сформу- лирована возможность создания сред с отри-

цательным коэффициентом поглощения. Анализируя особенности среды с отрицатель

ным поглощением, А. Фабрикант предложил

принцип усиления света. Эта идея применительно крадиочастотной области

спектра была реализована в 1955 г. Г. Басо-

Рис.24.2. вым, И. Прохоровым и независимо от них

Ч. Таунсом.

Выясним условия, при которых коэффициент поглощения среды становится отрицательным. Будем рассматривать идеализированный случай: будем полагать, что энергетические уровни атомов представляют собой линии. Это означает, что в каждом состоянии атом обладает определенной энергией и при оптических переходах между ними излучается или поглощается строго монохро­матический свет. В действительности это не так. Энергетические уровни атомов не являются линиями (рис. 24.3), а обладают шириной ΔE₁ и ΔE₂. В этом случае, согласно условию частот Бора, излучение атома при переходе из одного состояния в другое происходит не при одной частоте, а в некоторой области частот Δv, определяемой шириной энергетических уровней, между которыми осуществляются переходы.

Рис.24.3

Рассмотрим атом, находящийся в энергетических состояниях E₁ и Е₂, где через Е₁, Е₂ обозначены середины соответствующих уровней.

При взаимодействии атомов с электромагнитным излучением, как

известно, могут происходить два встречных процесса:

1. Атомы, находящиеся в основном состоянии Е₁, поглощая внешнее излучение с энергией hv=Е₂-Е₁ переходят из основного в возбужденное состояние. Вероятность такого процесса будет пропорциональной коэффициенту Эйнштейна В₁₂.

2. Атомы, находящиеся в возбужденном состоянии Е₂, подвергаясь действию внешнего излучения с энергией hv=Е₂-Е₁, вынужденным образом переходят в основное состояние, излучая при этом квант с энергией hv=Е₂-Е₁. Вероятность этого процесса будет пропорциональной коэффициенту Эйнштейна B₂₁.

Излучение, обусловленное спонтанными переходами атомов в основное состояние, не вносит существенного вклада в величину интенсивности лазерного излучения (τ велико) и поэтому при вычислении сум­марной интенсивности им можно пренебречь.

Таким образом, при прохождении параллельного пучка моно­хроматического излучения с объемной спектральной плотностью w(v) через слой вещества толщиной dx и единичного поперечного сече­ния изменение интенсивности выразится следующим образом:

dI = - B₁₂w (v,T) n₁hv dx + B₂₁w (v,T) n₂hv dx, (24.17)

где n₁ и п₂ — объемные концентрации атомов соответственно в состояниях Е₁ и Е₂ (см. (24.1)).

Первый член в формуле (24.17) выражает уменьшение, а второй — увеличение интенсивности света при его прохождении через среду толщиной dx благодаря процессам соответственно поглощения и вынужденного излучения. Поскольку В₁₂ = В₂₁ и w(v,T) = I/c, где c − скорость распространения света, то из (24.17) получаем:

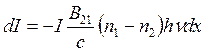. (24.18)

Принимая во внимание соотношение В₂₁ = 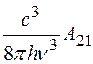между коэффициентами Эйнштейна (24.14), из (24.17) находим

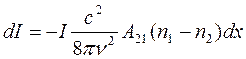. (24.19)

Учет ширины энергетических уровней. Выражение (24.19) полу­чено для бесконечно узких энергетических уровней, для которых линия поглощения, соответствующая переходу Е₁→E₂, настолько узкая, что объемную спектральную плотность излучения w(v,T) можно считать постоянной в пределах ширины этой линии поглощения. Однако, как уже мы отметили, энергетические уровни не являются бесконечно узкими, а обладают определенной шириной ΔE. Поэтому возникающие спектральные линии обладают определенным контуром, и мы фактически должны учесть наличие этого контура.

Поскольку в пределах контура линии разной частоты будут поглощаться по-разному, то коэффициенты Эйнштейна спонтанного перехода со второго уровня на первый в интервале частот dv запишем как α₂₁(v) dv. Аналогично, вероятности соответствующих вынужденных переходов запишем как

b₂₁ (v) w (v,T) dv и b₁₂ (v) w (v,T) dv.

Существует связь между интегральными коэффициентами Эйнштейна (A₂₁, В₂₁, В₁₂) и введенными дифференциальными коэффициентами, в частности,

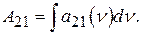
Поскольку A₂₁ имеет размерность с^-1, то, как следует из выше изло­женного, а₂₁ (v) — безразмерная величина.

Если выражение (24.19) описывает энергию поглощения во всей линии, то поглощение в интервале частот dv будет

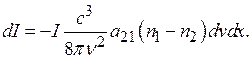(24.20)

Разделив обе стороны выражения (24.20) на Idv и произведя интег­рирование по х, получим

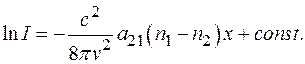(24.21)

Постоянную интегрирования можно определить из начального условия. Так как при х = 0 интенсивность падающего излучения I = I₀, то согласно (24.21) имеем: In I₀ = const. Учитывая это в (24.21), получим:

→

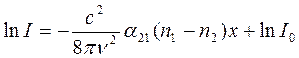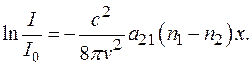
Отсюда

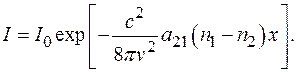(24.22)

Сравнивая (24.22) с формулой (24.16), получим выражение для коэффициента поглощения

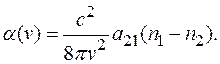(24.23)

Так как Е₂ > Е₁, то, как следует из (24.18), при термодинамическом равновесии всегда п₁ > п₂ и только при бесконечно высокой температуре

(Т → ) п₁ = п₂. Следовательно, в системе, находящейся в термодинамическом равновесном состоянии, невозможно отрицательное поглощение — усиление света. Чтобы имело место отрицательное поглощение, должно быть п₂ > п₁ т. е. число атомов в возбужденном состоянии больше, чем соответствующее число в основном состоянии, другими словами, должно иметь место как бы «обращенное» (инверсное) распределение атомов по энергетическим состояниям.

Инверсная населенность уровней. Если энергетические уровни системы удовлетворяют определенным условиям, то ее можно перевести в состояние с инверсной населенностью уровней. Процесс перевода системы в инверсное состояние называется накачкой. Накачку можно осуществить оптическими, электрическими и другими способами. При оптической накачке атомы, поглощая излучение, переходят в возбужденное состояние. При электрической накачке, например, в газообразной среде, атомы переходят в возбужденное состояние благодаря неупругим столкновениям атомов с электронами в газовом разряде. В этой связи следует еще раз отметить идею В. А. Фабриканта, выдвинутую в 1939 г., сущность которой заключалась в том, чтобы с помощью специальных молекулярных примесей избирательно исключить некоторые нижние энергетические состояния, в результате чего осуществилась бы инверсная заселенность.

Инверсное состояние иногда называют состоянием с «отрицательной температурой». Происхождение этого формального названия можно объяснить, пользуясь формулой Больцмана, которая определяет относительную заселенность энергетических уровней системы, находящейся в термодинамическом равновесии. В этом случае, как следует из (24.18),

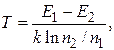(24.24)

откуда следует, что при п₂ > п₁ (так как Е₁ - Е₂ < 0) имеет место Т < 0. Это вовсе не означает, что температура системы становится ниже абсолютного нуля. «Отрицательная температура» формально выражает случай п₂ > п₁. Среда с такой инверсной заселенностью называется активной.

Из простых соображений следует, что для двухуровневой системы с помощью оптической накачки нельзя получить инверсную населенность.

Действительно, согласно распределению Больцмана, при тер­модинамическом равновесии всегда п₂ < п₁, и так как В₁₂ = В₂₁, то числа переходов атомов в единицу времени из состояния Е₁ в состояние Е₂ и наоборот будут одинаковыми. Следовательно, изменение числа атомов в основном и возбужденном состояниях благодаря вынужденным переходам не произойдет, т. е. каким было отношение п₁/п₂, таким оно останется при взаимодействии света с атомом, если, конечно, имеем дело, как об этом говорили, с двумя энергетическими уровнями атома — основным Е₁ и возбужденным Е₂. Таким образом, чтобы получить инверсную населенность, нужно использовать три или более энергетических уровня активной среды.

Усиление света с помощью трехуровневой системы. Рассмотрим трехуровневую схему накачки активной среды лазера (рис. 24.4,а). Четырехуровневая схема представлена на рис. 24.4,б.

Под действием оптического излучения с энергией hv = Е₃ — Е₁ атомы переходят из состояния Е₁ в состояние Е₃ (рис. 24.4,а). Из состояния Е₃ возможны спонтанные переходы в Е₂ и в Е₁. Из состояния Е₂, в свою очередь, возможны спон­танные переходы в состояние E₁.

Чтобы получить инверсную заселенность между уровнями Е₁ и Е₂, состояние Е₂ должно быть более долгоживущим по сравнению с состоянием Е₃, т. е. должны выполняться следующие условия:

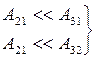. (24.25)

Рис. 24.4

Условия (24.25) означают, что вероятность спонтанного перехода атома с уровня 2 на уровень 1 гораздо меньше вероятностей спонтанных переходов как с уровня 3 на уровень 1, так и с уровня 3 на уровень 2. Следовательно, среднее время жизни атома в состоянии Е₂ должно быть гораздо больше, чем в состоянии Е₃, т.е.

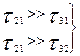, (24.26)

где времена жизни τ₃₁ и τ₃₂ на практике− величины порядка 10^-6 с, в то время как τ₂₁ ≈ 10^-3 с. Энергетическое состояние Е₂, удовлетворяющее этим условиям, называется метастабильным. Если на такую систему направить излучение достаточной мощности с частотой v = (Е₃ — E₁)/h, то с течением времени концентрация атомов п₂ на уровне 2 станет больше, чем концентрация атомов п₁ на уровне 1. При прохождении этих квантов через активную среду с инверсной населенностью будет происходить усиление излучения согласно формуле (24.23).

Можно получить инверсную населенность между уровнями Е₂ и Е₃, используя четырехуровневую схему (рис. 24.4,б).

Состояние Е₃ должно быть более долгоживущим по сравнению с состоянием Е₄. Тогда состояние Е₃ будет являться метастабильным. Если на такую среду направить излучение достаточной мощности с частотой v = (Е₄ — E₁)/h, то с течением времени концентрация атомов п₃ на уровне 3 станет больше, чем концентрация атомов п₂ на уровне 2.

В этой среде вследствие спонтанных переходов возникнут кванты с частотой v´ = (Е₃ — E₂)/h. При прохождении этих квантов через активную среду с инверсной населенностью также будет происходить усиление света согласно формуле (24.23).

Принцип усиления света в оптических квантовых генераторах по трех­уровневой схеме, который лежал в основе создания лазерных установок, был предложен Н. Г. Басовым и А. М. Прохоровым в 1955 г. Независимо от них аме­риканский физик Ч. Таунс с сотрудниками осуществил квантовый генератор электромагнитного излучения на молекулах аммиака. Эти работы советских и американских физиков положили начало бурному развитию квантовой электроники, за что им в 1964 г. была присуждена Нобелевская премия по физике.