Условие аналогии физических процессов

Задачи конвективного теплообмена могут быть решены в некоторых случаях аналитически; для сложного течения, включая турбулентность – экспериментально, хотя в настоящее время с учётом развития моделированной турбулентности – численно. Однако, необходимо постоянно согласовывать расчёт с экспериментальными данными и только в случае хорошего согласия использовать для прогнозирования.

Полезными оказываются результаты расчета процесса базируясь на методе аналогий.

Физические процессы, описывающие одинаковыми дифференциальными уравнениями, но имеющие разную физическую природу, называют аналогичными.

Можно говорить о тройной аналогии между переносом количества движения, количеством тепла и массы при определенных условиях течения.

Рассмотрим обтекание плоской пластины несжимаемой средой, когда градиентом давления вдоль пластины можно пренебречь и сила тяжести не оказывает влияния на течение. Физические свойства среды const. Уравнения движения, тепловой энергии, концентрационной диффузии запишутся как:

Уравнение движения:

.

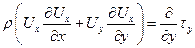(7.18)

Здесь

.

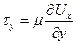(7.19)

Уравнение тепловой энергии:

.

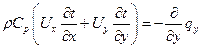(7.20)

Здесь

.

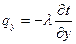(7.21)

Уравнение концентрационной диффузии:

.

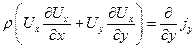(7.22)

Здесь

.

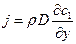(7.23)

j -поток массы, кг/м²с.

Если обеспечить одинаковые граничные условия для этих уравнений, то можно считать процессы подобными.

При отсутствии экспериментальных данных, например, для массоотдачи могут быть использованы данные по теплоотдаче или по сопротивлению трения.

Пример: при рассмотрении задачи массоотдачи в трубе можно воспользоваться данными по теплоотдаче:

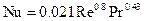
(7.24)

Здесь

.

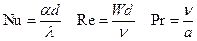(7.25)

Для массоотдачи выражение будет выглядеть так:

.

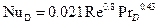(7.26)

Здесь

.

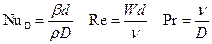(7.27)

β –коэффициент массоотдачи.

Если тройная аналогия имеет место, то опытные точки должны укладываться на одной прямой в координатах:

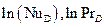
(7.28)