Конвективный теплообмен. Аналогия процессов ТМО

Конвективный перенос теплоты – перенос теплоты в среде с неоднородным распределением скорости и температуры, осуществлённый макроскопическими элементами среды в процессе их перемешивания:

.

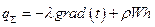(7.1)

Различают свободную (естественную) конвекцию – движение жидкости из-за разности плотностей ее нагретых и холодных слоев и вынужденную – под воздействием внешних сил (насоса - для жидкостей, вентилятора или компрессора – для газов.

Совместный процесс молекулярного (диффузия) и молярного (конвективного) перенос смеси, когда происходит выравнивание концентрации, называется массообменом.

Прежде чем записать систему решаемых уравнений сделаем замечания относительно потока среды. Считаем что среда, в которой длина свободного пробега частицы l, отнесённая к характерному размеру тела: 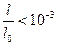( Число Кнудсена) является неразреженной и для нее можно использовать дифференциальные уравнения сохранения. В противном случае, среда будет разреженной, и частицы будут проскальзывать вдоль стенки. Для компонента скорости и температуры для неразреженной среды на стенке используется условие прилипания, т.е.:

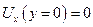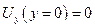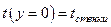
(7.2)

Тогда на стенке тепло передается только теплопроводностью:

.

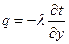(7.3)

Для расчета теплообмена между стенкой и окружающей жидкостью используется соотношение теплоотдачи (закон Ньютона-Рихмана):

,

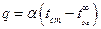(7.4)

где α - коэффициент теплоотдачи, Вт/м²К; t_cт - температуры стенки°С, t_ж - температура жидкости.

Из этих двух соотношений получим выражение для коэффициента теплоотдачи:

.

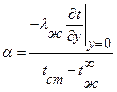(7.5)

Для расчета конвективного теплообмена необходимо решать систему уравнений: неразрывности, три уравнения движения, уравнение энергии.

Ниже приведена система уравнений конвективного теплообмена в обобщенном виде.

Уравнение неразрывности:

.

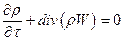(7.6)

Уравнение конвективной диффузии:

.

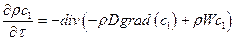(7.7)

Уравнение энергии:

.

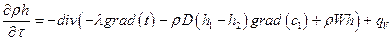(7.8)

Уравнение движения:

,

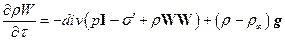(7.9)

где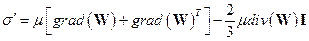

Приведенная система уравнений в приближении пограничного слоя записывается как обоснованно упрощенная.

Уравнение неразрывности:

.

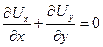(7.10)

Уравнение концентрационной диффузии (уравнение массоотдачи):

.

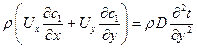(7.11)

Уравнение энергии:

.

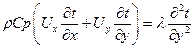(7.12)

Уравнение движения:

.

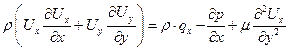(7.13)

Упрощения касаются оценки членов полных уравнений по порядку величин. При условии преобладающего движения , например, вдоль оси х, получали. При условии l>>δ получаем из уравнения неразрывности 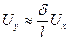, откуда:

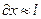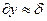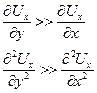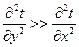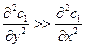
(7.14)

На основании этого упрощения уравнения (дифференциального) переноса теплоты до уровня модели или приближения пограничного слоя. Упрощение заключается в том, что некоторыми слагаемыми можно пренебречь.

Записанная выше система уравнений дает решение в тонком слое жидкости, называемом пограничном слое. В соответствии с рассматриваемой субстанцией (W,t,c₁) пограничные слои называются соответственно: гидродинамический, тепловой, диффузионный.

Толщиной гидродинамического пограничного слоя – называется тонкий слой жидкости, в котором скорость меняется от скорости стенки до скорости внешнего потока. За границу гидродинамического пограничного слоя принимается такая толщина слоя жидкости, в которой перепад скорости составляет 99% от полного перепада скорости:

.

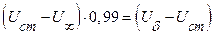(7.15)

В гидродинамическом пограничном слое происходит практически весь обмен импульсом. В гидродинамическом пограничном слое соизмеримы процессы переноса импульса (трения) вязкостью и конвекций.

Толщиной теплового пограничного слоя – называется тонкий слой жидкости, в котором температура меняется от температуры стенки до температуры внешнего потока. За границу теплового пограничного слоя принимается такая толщина слоя жидкости, в которой температурный напор состоит 99% от полного температурного напора:

.

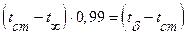(7.16)

В тепловом пограничном слое происходит практически весь теплообмен. В тепловом пограничном слое соизмеримы процессы переноса теплоты теплопроводностью и конвекций.

Подобным образом можно дать определение диффузионного пограничного слоя:

.

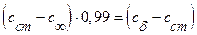(7.17)