Что такое Теплопередача
Передача теплоты через систему стенок от одной жидкости к другой называется процессом теплопередачи.
Уравнение теплопередачи:
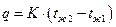
| (3.1) |
где K- коэффициент теплопередачи, 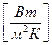 равен:
равен:
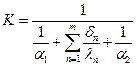
| (3.2) |
В предыдущей лекции мы получили решение для задач теплопередачи для плоских и цилиндрических стенок. Сейчас рассмотрим некоторые частные задачи, когда требуется управлять процессом теплопередачи, стремясь в одном случае уменьшить значение теплового потока (задача о тепловой изоляции), а в других случаях наоборот увеличить величину теплового потока (интенсификация теплопередачи, оребрение поверхностей).
Критический диаметр теплоизоляции
На практике теплоизоляционными называются материалы, теплопроводность которых не превышает величины 0,25 Вт/(мК).
● Естественная изоляция (природная): асбест, слюда, пробка и пр.
● Предварительно обработанная: асбестовая слюда, шлаковата, стекловата, пенопласт, пеношлакобетон и др.
Теплоизоляционные свойства последним из перечисленных материалов придает наличие в них мелких воздушных пузырьков или прослоек воздуха. В них из-за малости размеров, конвекция отсутствует и теплота передается только теплопропроводностью, порядок которой для воздуха при атмосферных условиях порядка 0,025 Вт/(мК), то есть на порядок ниже величины, приведенной выше для теплоизоляции.
Теплоизоляция плоских стенок может осуществляться любыми имеющимися под рукой материалами. Непродуманная теплоизоляция же цилиндрических труб может вызвать недоумение от полученного результата. Рассмотрим эту интригующую задачу. Итак, стенку трубы покрываем изоляцией.
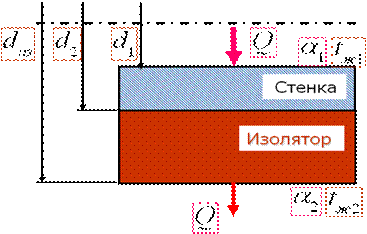
Теплоизоляция цилиндрической стенки
Линейная плотность теплового потока через двухслойную (толщина трубы и слой изоляции) цилиндрическую стенку равна:
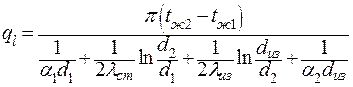
| (3.3) |
Здесь линейное термическое сопротивление теплопередачи через двухслойную цилиндрическую стенку равно:
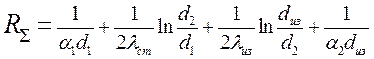
| (3.4) |
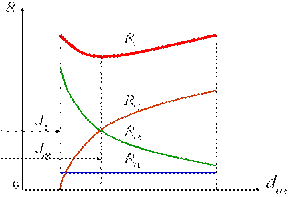
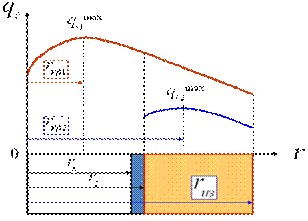
Из соотношения для линейного термического сопротивления видно, что с увеличением толщины слоя изоляции термическое сопротивление теплопроводности изоляции растет, сопротивление теплоотдачи (последнее слагаемое) падает. Следовательно, существует экстремальное значение суммарного термического сопротивления при dиз=var.
Для нахождения экстремума возьмем первую производную по dиз
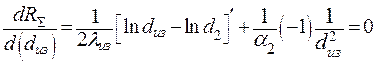
| (3.5) |
После сокращений получим
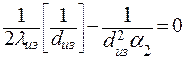
| (3.6) |
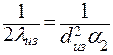
| (3.7) |
Откуда критический диаметр изоляции равен:
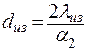 . .
| (3.8) | ||
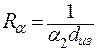 , , 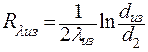
| 
| ||
Зависимость термических сопротивлений от диаметра трубы. Изменение линейной плотности теплового потока от радиуса
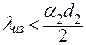 , то применение изоляции целесообразно, т.е. тепловые потери от трубы, покрытой такой изоляцией, будут сразу уменьшаться.
, то применение изоляции целесообразно, т.е. тепловые потери от трубы, покрытой такой изоляцией, будут сразу уменьшаться.
В противоположном случае теплоизоляция малоэффективна, и её применение приведёт к первоначальному увеличению тепловых потерь от трубы.
В случае установки двух слоев изоляции возникает вопрос какой из изоляционных материалов ставить непосредственно на трубу? Рассмотрим этот вопрос на практическом занятии.
Интенсификация процесса теплопередачи
Рассмотрим процесс теплопередачи в рекуперативном теплообменнике типа «труба в трубе» (Рис.3.). Внутри тонкостенной внутренней трубы движется горячая жидкость с такой скоростью, что при этом коэффициент теплоотдачи равен 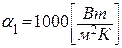 . В кольцевом зазоре движется газ с такой скоростью, что коэффициент теплоотдачи равен
. В кольцевом зазоре движется газ с такой скоростью, что коэффициент теплоотдачи равен 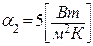 .
.
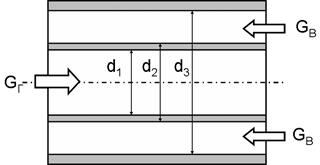
Принципиальная схема регенеративного теплообменника
Вычислим коэффициент теплопередачи для этого случая:
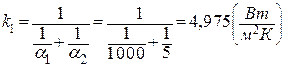
|
Применяя мероприятия с интенсификацией теплоотдачи со стороны жидкости и добившись при этом увеличения коэффициента теплоотдачи до величины 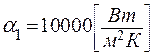 , то есть десятикратного увеличения снова вычислим коэффициент теплопередачи:
, то есть десятикратного увеличения снова вычислим коэффициент теплопередачи:
|
Как видно из оценочных расчетов интенсификацией теплоотдачи со стороны жидкости (со стороны большего коэффициента теплоотдачи) мы практически не изменили интенсивность процесса теплопередачи.
Увеличение же коэффициента теплоотдачи со стороны газа (меньшего коэффициента теплоотдачи) только в 2 раза привело к увеличению коэффициента теплопередачи примерно в 2 раза:
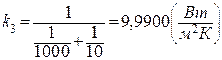 . .
|
Вывод напрашивается сам: мероприятия по интенсификации процесса теплопередачи следует проводить со стороны меньшего коэффициента теплоотдачи 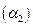 .
.
Однако это не единственный способ интенсифицировать теплопередачу. Запишем уравнение теплопередачи в виде:
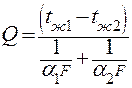
| (3.9) |
Как видно из данного уравнения можно увеличивать не только меньшее 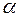 , но и поверхность теплообмена со стороны меньшего
, но и поверхность теплообмена со стороны меньшего 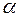 . Эти мероприятия связаны с оребрением поверхности со стороны меньшего коэффициента теплоотдачи. В рассматриваемом теплообменнике следует сделать оребрение на внешней поверхности внутренней трубы.
. Эти мероприятия связаны с оребрением поверхности со стороны меньшего коэффициента теплоотдачи. В рассматриваемом теплообменнике следует сделать оребрение на внешней поверхности внутренней трубы.
Рассмотрим задачу оребрения поверхности, когда ребра представляют собой плоские бесконечные тонкие пластины.

Оребренная поверхность
Физико-математическая постановка задачи: задача является стационарной двухмерной без внутренних источников теплоты. Рассмотрим тонкое ребро из материала с постоянным значением коэффициента теплопроводности. Отметим, что для тонких ребер температура основания ребра практически равна температуре поверхности стенки 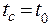 . Договоримся, что температура окружающей среды ниже температуры поверхности стенки трубы
. Договоримся, что температура окружающей среды ниже температуры поверхности стенки трубы 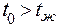 .
. 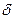 - толщина ребра, b – размер ребра в направлении
- толщина ребра, b – размер ребра в направлении 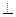 доске.
доске.
Уравнение сохранения тепловой энергии для рассматриваемого ребра запишется в виде:
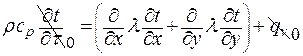 , ,
| (3.10) |
тогда
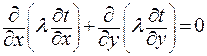 . .
| (3.11) |
Как видно из уравнения требуется поставить четыре граничных условия:
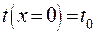 - граничное условие в основании ребра.
- граничное условие в основании ребра.
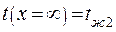 либо либо 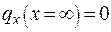 -граничное условие на конце ребра. -граничное условие на конце ребра.
|
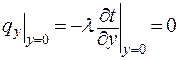 -граничное условие на оси ребра.
-граничное условие на оси ребра.
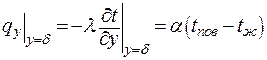 -граничное условие на боковой поверхности ребра.
-граничное условие на боковой поверхности ребра.
Произведем интегрирование уравнения теплопроводности по толщине ребра и сведем уравнение с частными производными к одномерному дифференциальному уравнению:
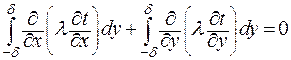
| (3.12) |
или
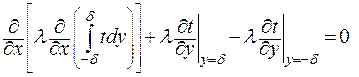 . .
| (3.13) |
Введем среднюю температуру по сечению ребра:
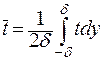 , ,
| (3.14) |
тогда
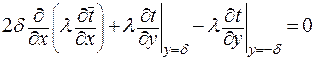 . .
| (3.15) |
Учитывая граничные условия:
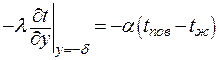 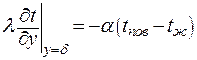
| (3.16) |
запишем
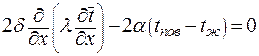 . .
| (3.17) |
Поскольку мы рассматриваем тонкое ребро с малым числом Био 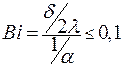 можно считать распределение температуры по сечению ребра равномерным, т.е.
можно считать распределение температуры по сечению ребра равномерным, т.е. 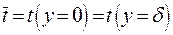 . Или:
. Или:
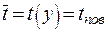 . .
| (3.18) |
С учетом равномерности профиля температуры по толщине ребра, уравнение теплопроводности запишется как:
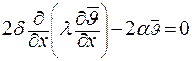 . .
| (3.19) |
Здесь 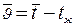 -избыточная температура.
-избыточная температура.
Или (3.19) представляется в виде:
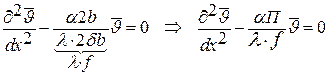 . .
| (3.20) |
Здесь f=2δb -площадь ребра, 2(δ+b) -периметр ребра равный 2(b) . вводя безразмерный параметр:
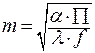 . .
| (3.21) |
Окончательно получим:
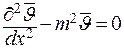 . .
| (3.22) |
С граничными условиями
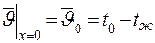 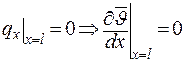 . .
| (3.23) |
Решение уравнения теплопроводности для ребра записывается как:
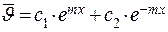
| (3.24) |
Подставляя в решение граничные условия, получим для ,бесконечного ребра 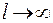 :
:
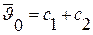
| (3.25) |
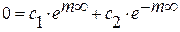
| (3.26) |
Из физических соображений получаем:
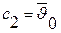 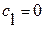 . .
|
Окончательное решение уравнения теплопроводности для  ребра записывается как:
ребра записывается как:
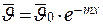 . .
| (3.27) |
Определим количество теплоты, снимаемое с бесконечного ребра. С боковой поверхности ребра снимается столько теплоты, сколько проходит через сечение основания ребра. Следовательно:
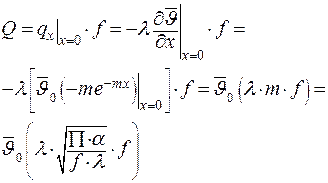
| (3.28) |
Окончательно:
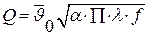 . .
| (3.29) |
Теплопроводность для ребра конечной длины
Для ребра конечной длины решаемое уравнение и решение его то же самое:
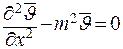 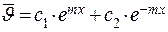 . .
| (3.30) |
Граничное условие в основании ребра не изменилось:
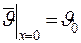 . .
|
На конце конечного ребра считаем, что плотность теплового потока пренебрежимо мала по сравнению с теплотой, снимаемой с боковой поверхности 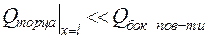 :
:
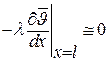 . .
| (3.31) |
Заготовим выражение для первой производной:
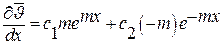 . .
| (3.32) |
Подстановка граничных условий в решение дает два уравнения для нахождения двух констант исходного уравнения:
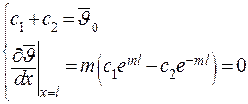
| (3.33) |
Константы равны:
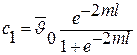 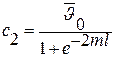 . .
| (3.34) |
Подставляя их в общее решение, получим:
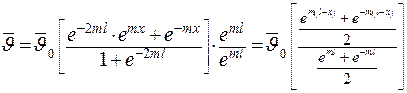 . .
| (3.35) |
Окончательно:
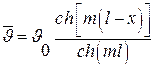 . .
| (3.36) |
При значении х равном длине ребра, получаем температуру на конце ребра:
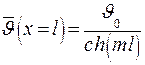 . .
| (3.37) |
Определим количество теплоты, снимаемое с конечного ребра длиной l. С боковой поверхности ребра снимается столько теплоты, сколько проходит через сечение основания ребра. Следовательно:
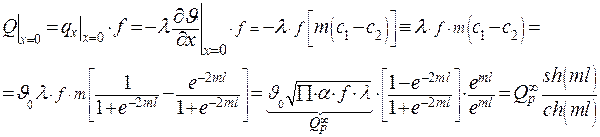
|
| Окончательно: | |
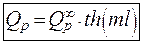
| (3.38) |
Эффективность ребра
Под эффективностью ребра понимают величину равную отношению количества теплоты снимаемого с реального ребра к количеству теплоты снимаемому с идеального ребра. Какое ребро может считаться идеальным – то вдоль которого температурный напор максимален и не изменяется. Это возможно при 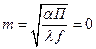 .
.
Вычислим эффективность Е тонкого плоского конечного ребра прямоугольной формы:
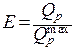 . .
| (3.39) |
Подставляя значения потоков теплоты, получим:
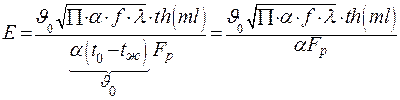 . .
| (3.40) |
Здесь Fp-боковая поверхность ребра:
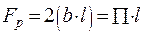
| (3.41) |
Окончательно получаем:
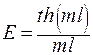 . .
| (3.42) |
| <== предыдущая лекция | | | следующая лекция ==> |
| Для начала рассмотрим простейшую задачу. | | | Что такое Нестационарная теплопроводность |
Дата добавления: 2017-10-04; просмотров: 2632;

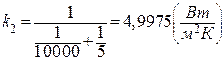 .
.










