Для начала рассмотрим простейшую задачу.
Дифференциальное уравнение теплопроводности и краевые условия
Запишем без вывода обобщенное уравнение нестационарной теплопроводности
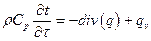
| (2.1) |
Левая часть уравнения представляет собой изменение внутренней энергии тела, первое слагаемое в правой части изменение теплоты поступившей через границу тела, вторе слагаемое – внутренние источники теплоты.
Уравнение является уравнением первого порядка по времени и второго порядка по пространственным координатам. Следовательно для однозначного решения данного типа уравнения требуется поставить краевые условия ( в количестве 7 в общем случае). Т.е. по времени поставить одно краевое (начальное) условие. По координатам по два краевых условия (граничных условия) на каждую координату. Следует отметить, что граничные условия могут быть поставлены либо по одному на каждой границе, либо два условия на одной границе.
Граничные условия подразделяют на четыре типа:
Граничные условия 1-го рода: на границе задается фиксированное значение температуры или закон ее изменения
Граничные условия 2-го рода: на границе задается фиксированное значение плотности теплового потока или закон его изменения
Граничные условия 3-го рода: на границе задаются условия теплоотдачи между стенкой и контактирующей с ней жидкостью, а также значение температуры жидкости.
Граничные условия 4-го рода: на границе ставятся условия сопряженя для тепловых потоков.
Для начала рассмотрим простейшую задачу.
Стационарная теплопроводность в плоской бесконечной пластине
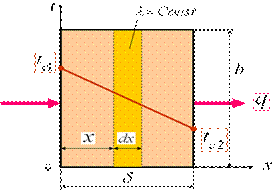
Теплопроводность через плоскую стенку
Условие стационарности:
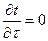
| (2.2) |
Условие одномерности:
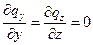 или при или при 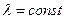 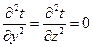
| (2.3) |
Уравнение сохранения тепловой энергии запишется в виде:
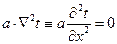
| (2.4) |
При постановке на поверхностях стенки граничных условий первого рода
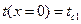 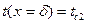
| (2.5) |
Получим
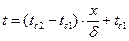
| (2.6) |
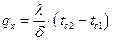
| (2.7) |
где 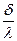 - термическое сопротивление теплопроводности.
- термическое сопротивление теплопроводности.
Система плоских стенок с граничными условиями I-го рода
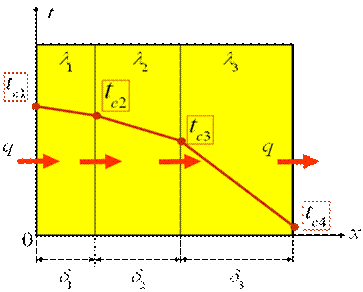
Теплопроводность через систему плоских стенок
(на примере трех стенок)
Используя ранее полученное решение для каждой из стенок, запишем:
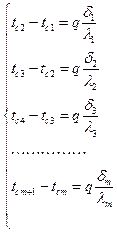
| (2.8) |
m - всего тел, n – текущая стенка.
Сложим левые и правые части системы. Учитывая, что 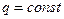 , получаем
, получаем
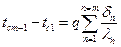 или или 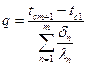
| (2.9) |
соотношения для расчета температуры в любой точке системы и плотности теплового потока через систему плоских пластин.
Система плоских стенок с граничными условиями III-го рода
В отличии от предыдущей задачи появилось еще два уравнения, учитывающих потерю температурного напора на термических сопротивлениях теплоотдачи.
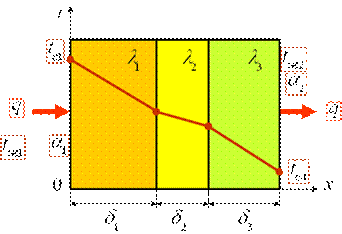
Стационарная теплопроводность при граничных условиях 3-го рода
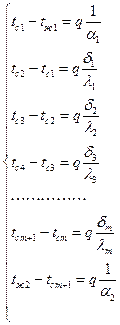
| (2.10) |
Сложим левые и правые части системы. Учитывая, что 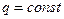 , получаем
, получаем
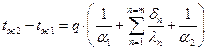 или или 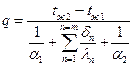
| (2.11) |
Здесь 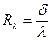 - термическое сопротивление теплопроводности,
- термическое сопротивление теплопроводности,
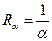 - термическое сопротивление теплоотдачи.
- термическое сопротивление теплоотдачи.
Распределение температуры в плоской стенке для случая, когда 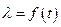 является функцией температуры
является функцией температуры
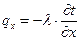 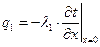 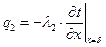
| (2.12) |
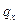 = = 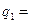 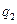
| (2.13) |
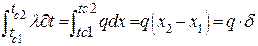
| (2.14) |
Вводя понятие среднеинтегрального значения коэффициента теплопроводности:
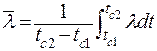 , ,
| (2.15) |
получим решение
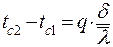
| (2.16) |
Получим среднеинтегральное значение при линейной зависимости коэффициента теплопроводности от температуры 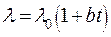 :
:
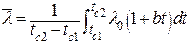
| (2.17) |
После интегрирования получаем
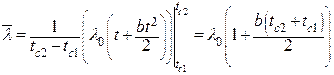
| (2.18) |
Можно записать как
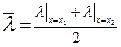 , ,
| (2.19) |
так как
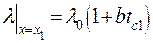 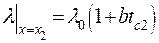
| (2.20) |
Получим распределение температуры по толщине пластины :
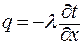
| (2.21) |
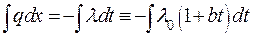
| (2.22) |
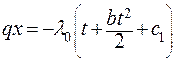
| (2.23) |
Откуда
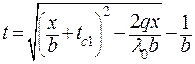
| (2.24) |
Стационарная теплопроводность через цилиндрическую стенку
Обобщенная запись стационарного уравнения теплопроводности в декартовой, цилиндрической, сферической системах координат имеет вид:
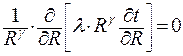
| (2.25) |
Для плоской бесконечной пластины:
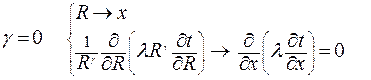
| (2.25а) |
Для круглого бесконечного цилиндра:
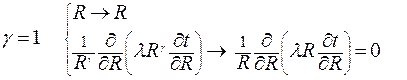
| (2.25б) |
Для сферической поверхности:
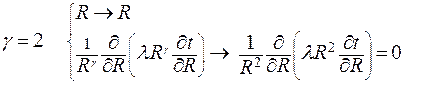
| (2.26в) |
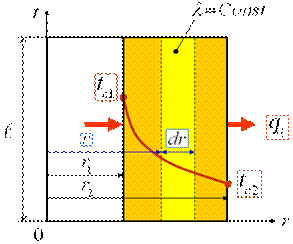
Теплопроводность через однослойную цилиндрическую стенку трубы
Для стационарной теплопроводности значения тепловых потоков на внутренней и внешней поверхности трубы равны между собой:
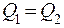
| (2.27) |
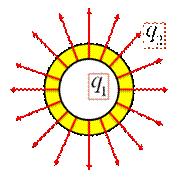
Плотность теплового потока на внутренней и внешней поверхности трубы
При этом плотность теплового потока на внутренней поверхности трубы q1 больше плотности теплового потока на внешней поверхности трубы q2
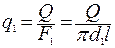 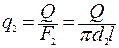
| (2.28) |
Здесь
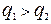
|
Это видно из соотношений (2.) и Рис.2.2, где густота линий плотности теплового потока по мере приближения к внешней поверхности трубы уменьшается. Для практических расчетов удобнее величина линейной плотности теплового потока. Последняя вводится как:
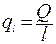
| (2.29) |
Эта величина является постоянной на каждой поверхности изотермы трубы. Линейная потность теплового потока связана с плотностью теплового потока соотношением:
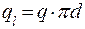
| (2.30) |
Теперь приступим к решению поставленной задачи. Нужно отметить, что часто в учебной литературе при решении этой задачи используется запись уравнения (2.25б) в виде
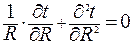
| (2.31) |
что не удобно для анализа и решения самого уравнения. Каждое из слагаемых лишено физического смысла. Между тем запись (2.25б) в виде
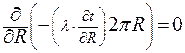
| (2.32) |
позволяет увидеть, что физический смысл этого соотношения в том, что линейная плотность теплового потока постоянна (не меняется в зависимости от радиуса)
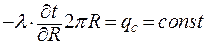
| (2.33) |
Решение получается достаточно просто
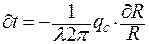
| (2.34) |
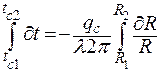
| (2.35) |
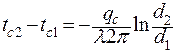
| (2.36) |
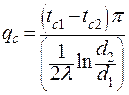
| (2.37) |
где 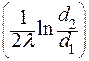 - линейное термическое сопротивление теплопроводности цилиндрической стенки
- линейное термическое сопротивление теплопроводности цилиндрической стенки
Если толщина трубы намного меньше наименьшего диаметра, 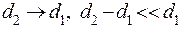 , то можно пользоваться формулами для плоской стенки.
, то можно пользоваться формулами для плоской стенки.
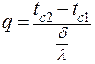
| (2.38) |
Действительно:
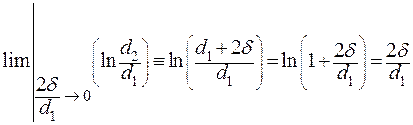
| (2.39) |
В этом случае
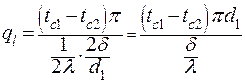
| (2.40) |
Учитывая, что при 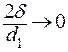
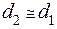
|
Получаем соотношение 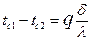 , что и требовалось показать.
, что и требовалось показать.
| <== предыдущая лекция | | | следующая лекция ==> |
| Вывод уравнения теплопроводности | | | Что такое Теплопередача |
Дата добавления: 2017-10-04; просмотров: 1692;











