Что такое Нестационарная теплопроводность
Уравнение нестационарной теплопроводности в обобщенном виде записывается как:
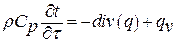 . .
| (4.1) |
Рассмотрим задачу прогрева (охлаждения) плоской бесконечной пластины. Объемное тепловыделение отсутствует. Физические свойства пластины не зависят от температуры (константа). Задача решается в следующей постановке: плоская (толщиной 2δ) бесконечная пластина помещена в жидкость с заданной температурой и условиями теплоотдачи (задан коэффициент теплоотдачи α). Требуется определить температуру в любой точке, в любое время.
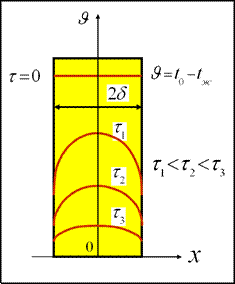
Охлаждение пластины
Уравнение нестационарной теплопроводности в этом случае:
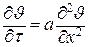 . .
| (4.2) |
Здесь 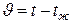 (относительный недогрев пластины).
(относительный недогрев пластины).
Краевые условия:
 . .
| (4.3) |
Будем искать решение в виде: 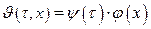 . Тогда уравнение нестационарной теплопроводности запишется как:
. Тогда уравнение нестационарной теплопроводности запишется как:
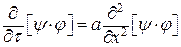 или или 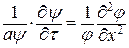 . .
| (4.4) |
Левая и правая часть уравнения являются функциями независимых переменных, поэтому они могут быть равны только константе. Причем из физических соображений константа должна быть отрицательной. Тогда дифференциальное уравнение распадается на два обыкновенных дифференциальных уравнения:
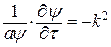 и и 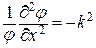 . .
| (4.5) |
Тогда
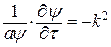 и и 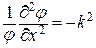 . .
| (4.6) |
Обозначим: 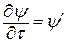 ,
, 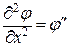 и запишем уравнения в виде:
и запишем уравнения в виде:
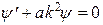 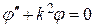 . .
| (4.7) |
Их решением являются соотношения:
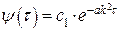 и и 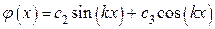 . .
| (4.8) |
Таким образом:
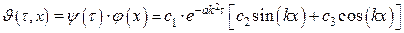 . .
| (4.9) |
Или, если ввести константы В=с1с2 и А=с1с3, то получим:
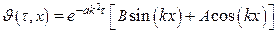 . .
| (4.10) |
Для нахождения трех констант А, В и k используем три краевых условия, записанных ранее. Используя граничное условие на оси пластины q=0 ( 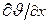 =0), получим:
=0), получим:
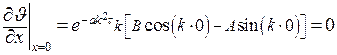 . .
| (4.11) |
Откуда следует, что В=0 и решение принимает вид:
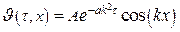 . .
| (4.12) |
Для нахождения константы k используем граничное условие на поверхности пластины: 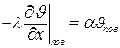 . Учитывая, что
. Учитывая, что
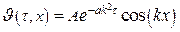 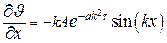 . .
| (4.13) |
Получим:
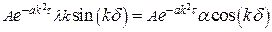 . .
| (4.14) |
Или после упрощений
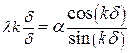 . .
| (4.15) |
Введем новую константу μ=kδ, тогда получаем:
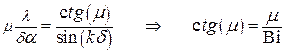 . .
| (4.16) |
Здесь Bi –отношение термических сопротивлений теплопроводности и теплоотдачи:
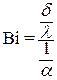 . .
| (4.17) |
Уравнение для определения является трансцендентным, имеет бесчисленное множество корней, которые могут быть получены только численно.
В предельных случаях Bi корни находятся аналитически.
При 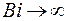 , если
, если 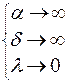 корни
корни 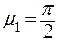 ;
; 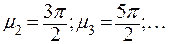
Или в обобщенном виде:
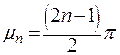 . .
| (4.18) |
При 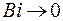 , если
, если 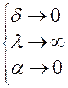 корни
корни 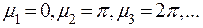
Или в обобщенном виде:
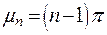 . .
| (4.19) |
При проведении расчётов: если 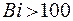 , то берётся решение для
, то берётся решение для 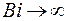
Если 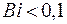 , то берётся решение для
, то берётся решение для 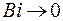 .
.
Общим решением нестационарного уравнения теплопроводности будет суперпозиция частных решений:
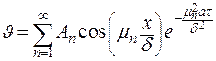 . .
| (4.20) |
Здесь 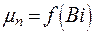 .
.
Неизвестными в этом решении остаются постоянные коэффициенты Аn, которые могут быть найдены при использовании начального условия 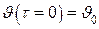 .
.
Процедура получения констант 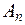 из начального условия следующая: умножаем левую и правую части уравнения (для начального момента времени)
из начального условия следующая: умножаем левую и правую части уравнения (для начального момента времени)
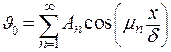
| (4.21) |
на
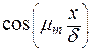 . .
|
Получим
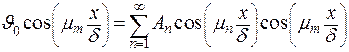 . .
| (4.22) |
Проинтегрируем это выражения по 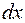 в интервале от -δ до δ
в интервале от -δ до δ
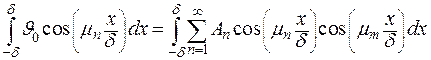 , ,
|
учитывая при этом, что:
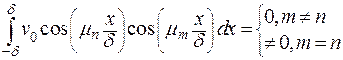 . .
|
Получим:
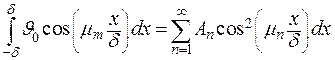 . .
| (4.23) |
Откуда коэффициенты равны:
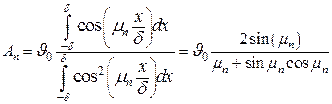 . .
| (4.24) |
Окончательное решение:
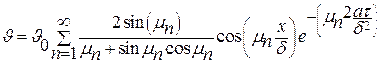 . .
| (4.25) |
Запишем решение в безразмерной форме:
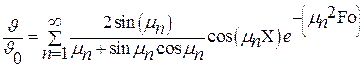 . .
| (4.26) |
Прежде чем приступать к анализу решения, запишем расчетные соотношения и конечное решение для прогрева круглого бесконечного цилиндра.
Уравнение нестационарной теплопроводности в бесконечном цилиндре:
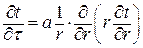 . .
| (4.27) |
Соотношение для расчета Bi:
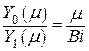 . .
| (4.28) |
Заметим, что вместо cos появилась функция Бесселя I-го рода, 0-порядка, вместо sin появилась функция Бесселя I-го рода, 1-порядка.
Решение:
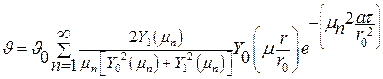 . .
| (4.29) |
Запишем решение в безразмерной форме:
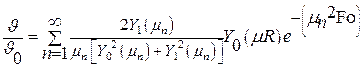 . .
| (4.30) |
Решение задачи о прогреве сферы сводится к решению задачи прогрева пластины, если перейти от функции температуры к величине равной умножению температуры на радиус сферы, т.е. 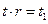 .
.
Анализ полученного решения на примере плоской бесконечной стенки.
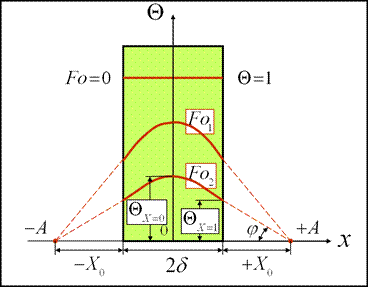
Температурное поле в пластине
Записывая граничное условие на поверхности пластины в виде:
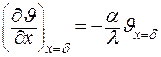 . .
| (4.31) |
и геометрическую трактовку производной в той же точке x=δ и приравнивая их между собой
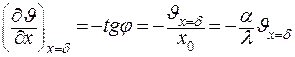 . .
| (4.32) |
получим:
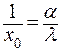 . .
| (4.33) |
Вводя безразмерное значение X0=x0/δ получаем:
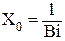 . .
| (4.34) |
Для любого момента времени касательная пересекается с осью x в точке x0.
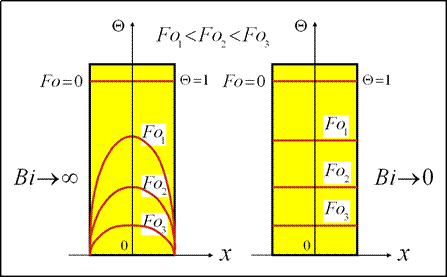
Охлаждение пластины
Левый рисунок -Внутренняя задача. Правый рисунок -Внешняя задача
Из рисунка видно, что при больших числах Bi, стремящихся к бесконечности, температура поверхности пластины равна температуре окружающей среды. Процесс теплоотдачи в этом случае лимитирует термическое сопротивление теплопроводности –задача является внутренней. При малых числах Bi, стремящихся к нулю, температура внутри пластины равномерно распределена. Процесс теплоотдачи в этом случае лимитирует термическое сопротивление теплоотдачи –задача является внешней.
Дата добавления: 2017-10-04; просмотров: 3194;











