Непрерывных сигналов
В качестве критерия оптимальности при приеме непрерывных сигналов принимают минимум среднеквадратического отклонения между переданным u(t) и принятым uпр(t) сигналами [13]:
min ε2u(t) = min[uпр(t) - u(t)]2.
Этот критерий учитывает не только помехи, но и искажения принимаемых сигналов. Минимально возможное значение среднеквадратической ошибки min ε2u(t) при заданных условиях передачи определяет потенциальную помехоустойчивость приема непрерывных сигналов. Физически min ε2u(t) означает мощность помехи, поэтому расчет потенциальной помехоустойчивости сводится к вычислению минимально возможной мощности помехи на демодуляторе. Абсолютное значение мощности помехи не может быть объективной характеристикой ее влияния на сигнал, так как надо учитывать еще и уровень сигнала. Поэтому оценку помехоустойчивости приема непрерывных сигналов можно произвести количеством информации, получаемой при приеме этих сигналов.
Для рассматриваемой радиотехнической системы морской связи непрерывный сигнал может быть частотно-модулированным, его можно представить в виде ряда Котельникова. Для этого сигнала ранее найдено отношение сигнал/помеха: 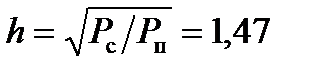 . В качестве помехи примем белый шум со спектральной плотностью N0 = 10-5В2/Гц;
. В качестве помехи примем белый шум со спектральной плотностью N0 = 10-5В2/Гц;
ширина полосы частот сигнала Δf = 3,0 кГц. Требуется определить количество информации при передаче сигнала по каналу связи.
Определим мощность помехи на входе приемного устройства:
Pп = N0Δf = 10-5 ∙ 3,0 ∙ 103 = 3,0 ∙ 10-2 Вт.
Среднеквадратическое отклонение помехи составит:
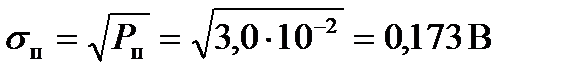 .
.
Найдем математическое ожидание напряжения сигнала:
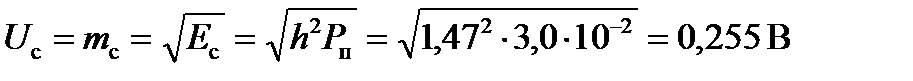 .
.
Вероятность ошибки при появлении одного отсчета на входе приемника составит:
Pош = 0,5ехр(-0,5h2) = 0,5ехр(-0,5∙1,472) = 0,017.
Это же можно записать и в виде
Pош =Ф*((∞ - mп)/σп) - Ф*((l - mп)/σп) = 1 - Ф*(l/σп) = 0,017,
где l – порог обнаружения; mп = 0 – математическое ожидание помехи.
Следовательно,
Ф*(l / σп) = 1 - 0,17 ≈ 0,83.
По таблице нормального распределения [3] находим Ф*(l/σп)≈ 0,83. Тогда
l/σп = 0,96; l = 0,96∙σп = 0,96∙0,173 = 0,166.
Вероятность отсутствия ошибки при приеме составит:
Pпр = 1 - Pош = 1 - 0,17 ≈ 0,83,
Pпр =Ф*((∞ - mс)/σс) - Ф*((l - mс)/σс) = 1 - Ф*((0,166 - 0,255)/σс).
После преобразования получим:
Ф*(-0,089/σс) = 1 - Pпр = 0,83.
По таблице нормального распределения находим:
Ф*(-0,089/σс) = Ф*(-0,96) ≈ 0,83,
-0,089/σс = -0,096, σс = 0,093.
Количество информации на один отсчет определяется по формуле
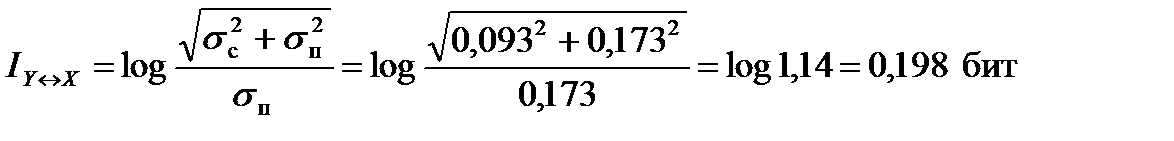 .
.
Дата добавления: 2017-10-04; просмотров: 1450;











