Выигрыш в отношении сигнал/помеха

Другим способом определения помехоустойчивости приема непрерывных сигналов является вычисление отношения средних мощностей сигнала P_c и помехи Р_п на выходе демодулятора

h_вых = P_c / Р_п.

В любом демодуляторе отношение сигнал/помеха на выходе h_вых зависит не только от качественных показателей демодулятора, но и от отношения сигнал/помеха на его входе h_вх. Помехоустойчивость систем передачи непрерывных сигналов оценивают выигрышем в отношении сигнал/помеха:

g = h_вых / h_вх = (P_{c вых} / Р_{п вых}) / (P_{c вх} / Р_{п вх}),

причем средние мощности помех на входе и выходе демодулятора определяются в полосе частот сигналов.

Выигрыш g показывает изменение отношения сигнал/помеха демодулятором. При g > 1 демодулятор улучшает отношение сигнал-помеха, при g < 1 получается не «выигрыш», а «проигрыш».

Расчетные формулы выигрыша для оптимального демодулятора при различных видах модуляции и помехе в виде аддитивного белого гауссовского шума приведены в таблице 22.3 где обозначены: K_A² =10 lg P_max/P; α = Δf_c/F_m – коэффициент расширения полосы, показывающий, во сколько раз ширина спектра модулированного сигнала Δf_c превышает максимальную частоту модулирующего сигнала F_m; M – коэффициент модуляции; т - индекс модуляции; К_A – коэффициент амплитуды модулирующего сигнала, представляющий собой отношение его максимальной мощности к средней и определяемый в логарифмических единицах по формуле (табл. 22.3).

Таблица 22.3

Расчетные формулы выигрыша оптимального демодулятора

при различных видах модуляции

Вид	Выигрыш	Вил	Выигрыш
AM		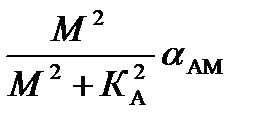ЧМ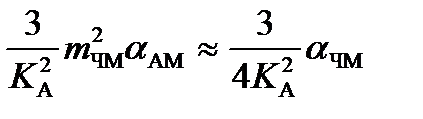
БМ	αБМ = 2	ФМ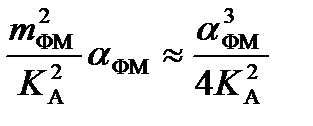
ОМ	αОМ = 1	АИМ-AM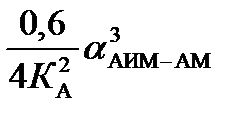
АИМ	αАИМ	ФИМ-АМ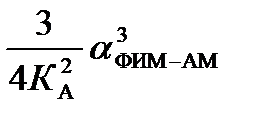

Анализ формул таблицы 22.3 показывает, что для AM максимальный выигрыш g_АМ = 0,666 достигается при М = 1 и K_A² = 2. Практически всегда М < 1 и K_A² = 2, поэтому g_АМ < 0,666, т. е. система с AM не обеспечивает «выигрыш». Физически малый выигрыш для AM объясняется тем, что большая часть мощности модулированного сигнала сосредоточена в несущей частоте, а полезная информация, создающая сигнал на выходе детектора, содержится в маломощных боковых колебаниях. Поэтому устранение несущей в АМ-сигнале (переход к БМ и ОМ) увеличивает выигрыш до значения g = α.

В широкополосных видах модуляции (ЧМ, ФМ, ФИМ и др.) выигрыш может быть намного больше единицы и резко возрастает при расширении спектра модулирующего сигнала (кубическая зависимость от коэффициента расширения полосы α). В связи с этим для увеличения выигрыша следует повышать девиацию частоты угловых модуляций или уменьшать длительность импульса несущей импульсных модуляций.

Формулы выигрыша являются исходными как для определения качества приема непрерывных сигналов, так и для сравнения различных систем передачи по помехоустойчивости.

Для рассматриваемой радиотехнической системы морской связи определим отношение сигнал/помеха на выходе демодулятора АМ-сигналов, если отношение сигнал/помеха на его входе h_вх = 1,47 дБ. При этом параметры модуляции следующие: М = 0,6; коэффициент амплитуды K_A = 14 дБ. При приеме используется фильтр, согласованный со спектром сигнала.

Подставив в формулу выигрыша AM параметры модуляции (m_AМ = 0,6 и K_A² = 2, α = 2), получим:

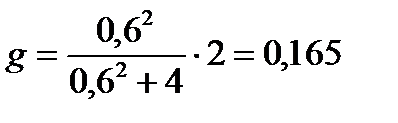
Тогда h_вых = g∙h_вх = 0,165∙1,47 = 0,243.

В логарифмических единицах h_вых =10∙lg 0,243 ≈ -6,1 дБ, т.к. g < 1 – это свидетельствует о проигрыше демодулятора.

Для рассматриваемой радиотехнической системы морской связи определим отношение сигнал/помеха на выходе демодулятора ЧМ-сигналов, если отношение сигнал/помеха на его входе h_вх = 1,47 дБ. При этом параметры модуляции следующие: m_ЧМ =10, коэффициент амплитуды К_A = 14 дБ, прием оптимальный.

Подставив в формулу выигрыша ЧМ параметры модуляции m_ЧМ =10 и K_A² = 10^1,4 = 25,1, α ≈ 2∙Δf / F_m = 2∙3∙10³/(3,4∙10³) = 1,77,

получим:

.

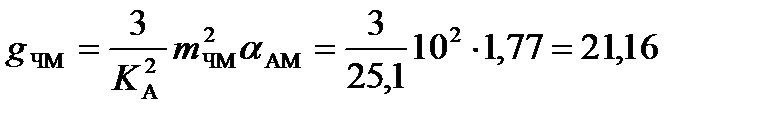Тогда h_вых = g∙ h_вх = 21,16∙1,47 = 31,1. В логарифмических единицах h_вых =10∙lg 31,1 =14,93 дБ.

В общем случае при оптимальном приеме также имеет место проигрыш при применении АМ-сигналов по сравнению с ЧМ-сигналами для одинаковых условиях приема, т. е. равенстве мощностей модулированных сигналов и спектральной плотности мощности помех на входах приемников. При одних и тех же условиях отношение сигнал/помеха в системе с ЧМ не менее чем в (4,5∙m_ЧМ²) раз больше, чем в системе с AM. На практике в системах с ЧМ применяют, как правило, индекс модуляции m_ЧМ² ≥ 5, и тогда преимущество ЧМ по сравнению с AM весьма значительное. Это преимущество получается за счет расширения полосы занимаемых частот.

Выигрыш при применении модулированных сигналов объясняется когерентным сложением в демодуляторе спектральных составляющих сигнала. Сложение составляющих помех осуществляется некогерентно.

Однако из изложенного не следует, что для различных видов модуляции и больших значений коэффициента а достигаются огромные значения выигрыша. Так, для ЧМ при m_ЧМ = 60 и K_A² =2 можно получить выигрыш g = 6,6∙10⁵. Казалось бы, задача обеспечения высокого качества передачи непрерывных сигналов решается достаточно просто увеличением ширины спектра модулированного сигнала. Но с расширением спектра растет мощность помехи на входе демодулятора и соответственно снижается отношение сигнал/помеха h_вх. При некотором пороговом значении h_{вх пор} резко увеличивается уровень помех на выходе демодулятора, а отношение сигнал/помеха на выходе демодулятора скачкообразно уменьшается.

На рисунке 22.2 приведены кривые помехоустойчивости оптимальных демодуляторов при различных видах модуляции. Порогом помехоустойчивости демодулятора является минимальное отношение сигнал /помеха на его входе, ниже которого система передачи информации с заданной модуляцией теряет преимущество по помехоустойчивости. Пороговый эффект ограничивает возможность применения модуляций для повышения качества передачи непрерывных сигналов. Появление порога можно объяснить эффектом подавления сильным сигналом слабого в детекторе.

В надпороговой области сигнал превышает помеху, и в детекторе подавляется более слабая помеха. В подпороговой области помеха превышает сигнал, и в детекторе подавляется уже более слабый сигнал более сильной помехой. Пороговые явления начинают наблюдаться при равенстве пиковых значе­нии сигнала и помехи. Обычно коэффициент амплитуды помехи K_A ≈ 3, порог помехоустойчивости h_{вх пор} ≈ 10 дБ (рис. 22.2).

При синхронном детектировании AM, БМ, ОМ-сигналов пороговый эффект не наблюдается.

В настоящее время разработаны и внедрены методы снижения порога помехоустойчивости для систем передачи информации с ЧМ как наиболее распространенной. С этой целью используются следящие фильтры додетекторной обработки сигнала. Следящий фильтр имеет полосу пропускания меньше, чем ширина спектра модулированнго сигнала, и следит за мгновенной частотой ЧМ-сигнала, которая изменяется сравнительно медленно по закону модулирующего сигнала. Это позволяет уменьшить мощность помехи на выходе следящего фильтра примерно в m_ЧМ раз, что ведет к понижению порога на 5-7 дБ.

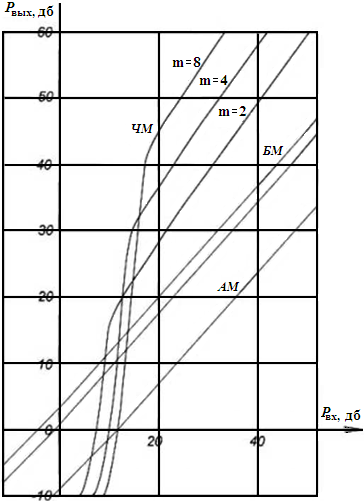
Рис. 22.2 Помехоустойчивость оптимальных демодуляторов при различных видах модуляции

Вместо следящего фильтра часто используют следящий гетеродин, частота которого изменяется синхронно с частотой принимаемого сигнала. При этом полоса пропускания фильтра промежуточной частоты остается неизменной: П ≈ 2F_m,где F_m – максимальная частота модулирующего сигнала.

Для рассматриваемой радиотехнической системы морской связи определим производительность источника дискретных сообщений при скорости передачи информации В = 50 Бод пятиэлементным двоичным кодом.

Для равновероятных букв вероятность одной буквы русского алфавита Р(а_i) = 1/32. В одной букве содержится I(a_i) = - log 1/32 = 5 бит информации. При коэффициенте избыточности русского текста v = 0,5 энтропия текста определится как Н(А) = 2,5 бит на букву. Длительность передачи одного символа находится по формуле t₁ = 1/B, а длительность передачи пяти символов и расстояния между буквами, т. е. одной буквы, по формуле t_б = 7,5/B = 7,5/50 = 0,15 с. Тогда производительность дискретного источника составит:

V(A) = H(A)/t_ср = 2,5/0,15 = 16,67 бит/с.