Количество информации при приёме дискретных сигналов радиотехнической системы связи
Для рассматриваемой радиотехнической системы морской связи найдем вероятность ошибки при оптимальных когерентном и некогерентном приемах двоичных AM, ЧМ и ФМ-сигналов, если отношение сигнал/шум по напряжению h = 1,47. В таблице 22.1 приведены значения вероятностей ошибок, вычисленные для различных видов сигналов и приёма.
Количество информации, получаемой при приеме двух равновероятных сигналов с вероятностями ошибки, соответствующими таблице 22.1, можно вычислить по формуле
I = Н0 - Н1,
где Н0 – априорная энтропия; Н1 – апостериорная энтропия.
Для двух равновероятных сигналов априорная энтропия вычисляется по формуле
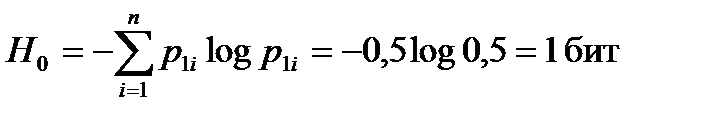 .
.
Для сигнала с амплитудной модуляцией апостериорная энтропия составляет:
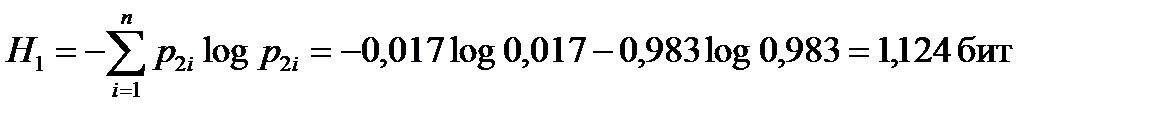 .
.
Количество информации определяется как
I = Н0 - Н1 = 1 - 0,124 = 0,876 бит.
Аналогично вычислено количество информации для сигналов с частотной и фазовой манипуляциями.
Таблица 22.1
Вероятность ошибок для различных видов сигналов и приёма
| Вид дискретных сигналов | Вероятность ошибки при когерентном приеме | Вероятность ошибки при некогерентном приеме |
| AM | 0,017 | 0,056 |
| ЧМ | 0,001 | 0,006 |
| ОФМ | 0,000003 | 0,000083 |
Результаты вычислений сведены в таблице 22.2. Результаты расчетов показывают, что предпочтительной является относительная фазовая манипуляция, позволяющая получить наибольшее количество информации при передаче сообщений.
Таблица 22.2
Количество информации для различных видов сигналов и приёма
| Вид дискретных сигналов | Количество информации при когерентном приеме, бит | Количество информации при некогерентном приеме, бит |
| AM | 0,876 | 0,69 |
| ЧМ | 0,982 | 0,94 |
| ОФМ | 0,999 | 0,999 |
Таким образом, сравнение помехоустойчивости различных видов манипуляции можно произвести по вероятности ошибки при передаче определенных сигналов, по количеству передаваемой информации на два переданных сигнала. Кроме этого, очень часто сравнение помехоустойчивости производится по энергетическому выигрышу, под которым понимают различие в энергиях сигналов, обеспечивающих одинаковое значение вероятности ошибки при различных видах манипуляции, способах приема, кодирования и т.д. Энергетический выигрыш определяется по формуле
gэ = 10∙lg(ES1 / ES2) при Рош = const, N0 = const,
где ES1, ES2 – соответственно энергии сигналов S1(t) и S2(t) .
Если gэ < 0 дБ, то имеются энергетические потери. Обычно значения энергий для расчета gэ находят по графическим зависимостям. Такие зависимости приведены на рисунке 22.1. Вероятность ошибки по оси ординат для удобства отложена в логарифмическом масштабе. Из графиков следует, что наибольшую помехоустойчивость имеет система с ФМ-сигналами, наименьшую – с АМ-сигналами. Проведя вычисления gэ, получим, что система с противоположными ФМ-сигналами дает энергетический выигрыш на 3 дБ (или в 2 раза) по сравнению с ортогональными ЧМ-сигналами и на 6 дБ (или в 4 раза) – по сравнению с АМ-сигналами. Физически это объясняется тем, что сигналы максимально отличаются друг от друга.
Для рассматриваемой радиотехнической системы морской связи определим энергетический выигрыш оптимального когерентного приема двоичных AM-сигналов по сравнению с оптимальным некогерентным приемом этих же сигналов. Пусть Рош =1,79∙10-2. Из точек пересечения прямой Рош =1,79∙10-2 зависимостей 4 (когерентный прием) и 5 (некогерентный прием) следует, что для обеспечения Рош =1,79∙10-2 при когерентном приеме необходимо h22 =10, а при некогерентном приеме h22 = 14. Энергия сигнала определится как E = h2N0, энергетический выигрыш составит:
gэ = 10∙lg(14/10) =1,46 дБ.
Для рассматриваемой радиотехнической системы морской связи определим энергетический выигрыш оптимального когерентного приема двоичных ЧМ сигналов по сравнению с оптимальным некогерентным приемом этих же сигналов. Пусть Рош =1,79∙10-2. Из точек пересечения прямой Рош =1,79∙10-2 зависимостей 2 (когерентный прием) и 3 (некогерентный прием) следует, что для обеспечения Рош =1,79∙10-2 при когерентном приеме необходимо h22 = 4,1, а при некогерентном приеме h22 = 6,1. Энергия сигнала определяется по формуле E = h22∙N0, энергетический выигрыш составит
gэ = 10∙lg(6,1/4,1) = 1,725 дБ.
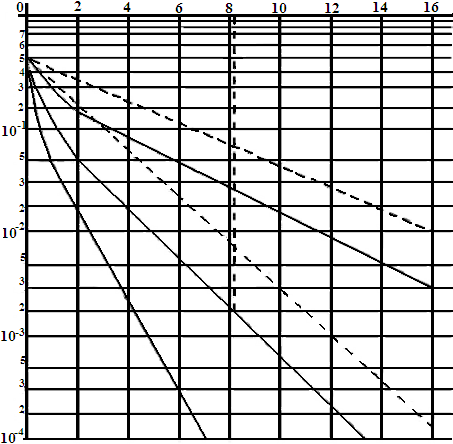
Рис. 22.1. Зависимость вероятности ошибок от отношения сигнал/помеха для различных видов модуляции (манипуляции)
Таким образом, для рассматриваемой радиотехнической системы морской связи энергетический выигрыш gэ оптимального когерентного приема двоичных ЧМ-сигналов но сравнению с оптимальным некогерентным приемом этих же сигналов равен 1,725 дБ.
Из примера хорошо видно, что энергетические потери некогерентного приема незначительны (1,46 дБ для AM и 1,725 для ЧМ), поэтому при практической реализации приемников АМ и ЧМ-сигналов целесообразно использовать более простой некогерентный приемник.
Дата добавления: 2017-10-04; просмотров: 1649;











