Метод быстрой свертки

Фильтрация сигналов может быть выполнена в частотной области путем вычисления спектральной плотности входного сигнала, умножения ее на КЧХ фильтра и выполнения обратного преобразования Фурье (на практике для входного сигнала, который представляет собой реализацию случайного процесса, можно вычислить только дискретное преобразование Фурье). Этот на первый взгляд сложный способ нахождения выходного сигнала оказывается на практике более эффективным в вычислительном отношении, чем прямое вычисление свертки, благодаря существованию алгоритмов быстрого преобразования Фурье. Метод КИХ-фильтрации на основе БПФ получил название метода быстрой свертки.

При его реализации необходимо учитывать следующие два обстоятельства. Первое состоит в том, что дискретное преобразование Фурье обладает двойственностью – оно соответствует как последовательностям конечной длины, так и периодическим последовательностям. По этой причине перемножение коэффициентов ДПФ двух последовательностей (входного сигнала и импульсной характеристики) соответствует не обычной (апериодической), а так называемой циклической (круговой) свертке.

Убедимся, что это действительно так.

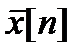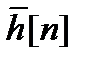Пусть и – периодические последовательности с периодом N. Их циклическая свертка определяется выражением

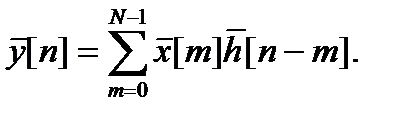
ДПФ результирующей последовательности

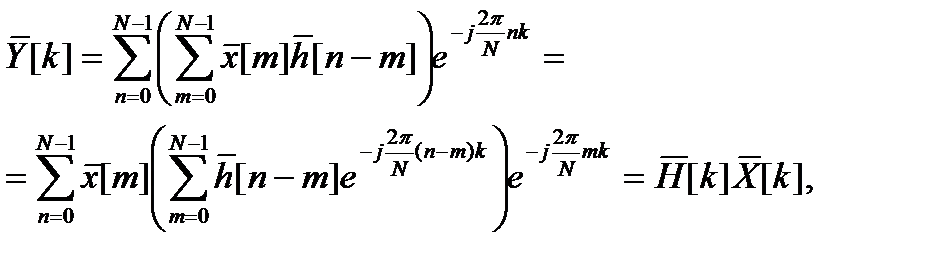(13.3)

,

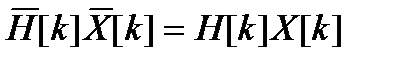где 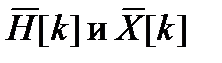находятся как ДПФ N-периодических последовательносте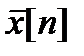й и 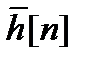, а H[k] и X[k] – как ДПФ их конечных фрагментов длины.

При выводе (13.3) учтен тот факт, что сумма в круглых скобках во второй строке равна 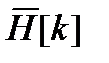независимо от m в силу периодичности суммируемых членов: при различных m суммируются одни и те же N слагаемых в разном порядке. Таким образом, видно, что циклическая свертка (или свертка периодических последовательностей) соответствует поточечному произведению ДПФ-спектров последовательностей. При фильтрации же должна выполняться обычная апериодическая свертка, определяемая выражением (13.2).

Преодолеть эту трудность можно следующим образом. Преобразование Фурье последовательности длины N дает полином (относительно e^-jω) степени N - 1. Полагая, что x[n] и h[n] – последовательности длины N, видим, что произведение их фурье-образов есть полином степени 2(N – 1). Но при поточечном перемножении ДПФ-спектров, имеющих по N отсчетов, получается всего N результирующих отсчетов, что соответствует полиному всего лишь (N – 1)-й степени. Единственный способ получения правильного результата умножения двух полиномов состоит в том, чтобы точек вычисления ДПФ «хватило» для представления результата. Иначе говоря, если используется N-точечное ДПФ, то степень результирующего полинома должна быть не выше (N – 1). Это, в свою очередь, означает, что сумма длин последовательностей x[n] и h[n] (обозначим их M и L) должна удовлетворять очевидному соотношению M - 1 + L - 1 ≤ N - 1 (или M + L - 1 ≤ N). Для того чтобы можно было для последовательности x[n] длины M < N получить N отсчетов ДПФ, следует перед вычислением ДПФ последовательность x[n] дополнить N - M нулевыми отсчетами (и то же проделать с другой последовательностью). Тогда результат их циклической свертки, полученный применением БПФ, совпадает с результатом апериодической свертки.

Второе обстоятельство, которое должно учитываться при реализации КИХ-фильтрации методом быстрой свертки, относится к фильтрации последовательностей большой (в частности, бесконечной) длины. Если длина входной последовательности велика (сотни тысяч отсчетов и более), что типично для обработки сигналов, применяемых в радиотехнике и связи, то необходимое основание БПФ (число вычисляемых отсчетов) оказывается слишком большим. Это влечет за собой высокие требования к объему оперативной памяти вычислителя БПФ, а также приводит к большой задержке результирующего сигнала (результат может быть получен не ранее чем поступит последний отсчет входной последовательности плюс время, необходимое для вычисления прямого БПФ, умножения и обратного БПФ). Для того чтобы снизить требования к памяти и уменьшить задержку, применяют секционирование свертки [7].

Пусть h[n] – импульсная характеристика фильтра, имеющая длину M, а x[n] – сигнальная последовательность бесконечной длины. Представим x[n] в виде

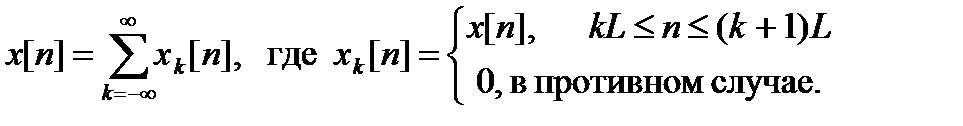
Нетрудно видеть, что таким образом входная последовательность разбивается (секционируется) на совокупность неперекрывающихся примыкающих друг к другу сегментов длиной L отсчетов каждый.

В силу билинейности свертки (линейности по каждому из операндов)

.

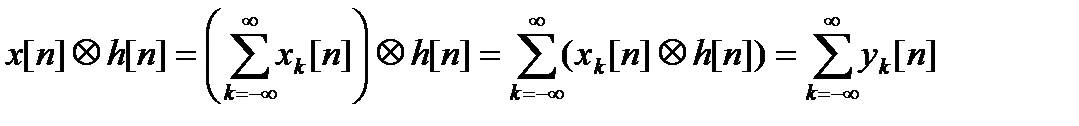Как видно из полученного выражения, свертка последовательности бесконечной длины с конечной импульсной характеристикой может быть точно заменена бесконечной суммой сверток сегментов фиксированной длины с этой же импульсной характеристикой. Каждая частичная свертка требует для своего вычисления (L + M – 1)-точечного БПФ. Поскольку L выбирается произвольно, секционирование позволяет реализовать КИХ-фильтрацию длинных (потенциально – бесконечно длинных) последовательностей; при этом результат y_k[n] фильтрации сегмента x_k[n] появляется с задержкой, определяемой временем прямого и обратного БПФ и умножения, но эта задержка теперь отсчитывается от момента окончания сегмента, а не всей последовательности.

Результат каждой частичной свертки имеет длину (L + M - 1), а следуют секции с относительным сдвигом L. Таким образом, результаты частичных сверток y_k[n] суммируются с перекрытием носителей kL ≤ n ≤ (k + 1) L + M - 1. Этот метод секционирования свертки известен как метод перекрытия с суммированием (overlap-add method) [7].

Альтернативный метод перекрытия с накоплением (overlap-save method) заключается в том, что перекрываются сегменты входной последовательности. Последовательность x[n] разбивается на секции x_k[n] длиной (L + M – 1), причем последние (M - 1) отсчетов каждой секции перекрываются с таким же количеством первых отсчетов следующей секции (M – по-прежнему длина импульсной характеристики, L выбирается произвольно). Каждая секция подвергается БПФ с основанием (L + M – 1). Импульсная характеристика длиной M дополняется нулями до основания БПФ. Результат фильтрации (циклической свертки) содержит всего (L + M – 1) отсчетов, из которых последние (M - 1) отсчетов – «ошибочные», не совпадающие с результатом апериодической свертки, а остальные L отсчетов являются «правильными». Суммируются результаты циклических частичных сверток после отбрасывания «ошибочных» отсчетов, т. е. секции выходной последовательности длиной L следуют друг за другом без перекрытия.