Моделирование конвективного теплообмена
Рассмотрим стационарный конвективный теплообмен между твердым телом и омывающей его несжимаемой вязкой жидкостью. При этом физические параметры будем считать зависящими от температуры и давления.
Для сокращения запишем уравнения конвективного теплообмена в векторной форме:
уравнение движения
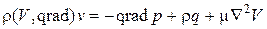 ; (4.117)
; (4.117)
уравнение сплошности
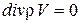 ; (4.118)
; (4.118)
уравнение переноса тепла или уравнение энергии
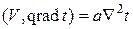 (4.119)
(4.119)
где 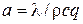 – коэффициент температуропроводности;
– коэффициент температуропроводности;
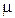 – коэффициент вязкости;
– коэффициент вязкости;
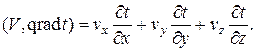
Параметры 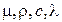 в общем случае являются переменными и зависят от температуры, т.е.:
в общем случае являются переменными и зависят от температуры, т.е.:
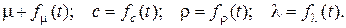 (4.120)
(4.120)
краевые условия будут
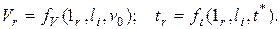 (4.121)
(4.121)
Составим масштабные преобразования и введя их в уравнения
(217)-(219) получим в конечном итоге систему уравнений связи:
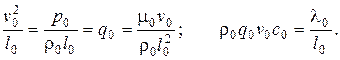 (4.122)
(4.122)
Из девяти масштабов, связанных четырьмя уравнениями (4.122), пять масштабов могут быть выбраны произвольно:
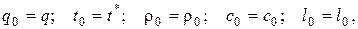 (4.123)
(4.123)
а остальные четыре определены из условия (4.123):
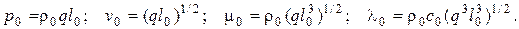 (4.124)
(4.124)
Равенства 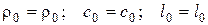 следует понимать в том смысле, что выбор указанных масштабов является произвольным.
следует понимать в том смысле, что выбор указанных масштабов является произвольным.
Выражения для безразмерных величин:
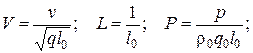
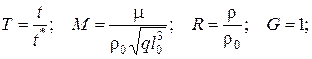
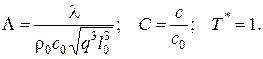
После этого дифференциальные и характеристические уравнения и краевые условия в безразмерном виде запишем следующим образом:
уравнение движения
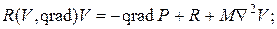 (4.125)
(4.125)
уравнение сплошности
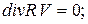 (4.126)
(4.126)
уравнение энергии
 (4.127)
(4.127)
характеристические уравнения:
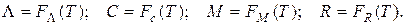 (4.128)
(4.128)
Краевые условия:
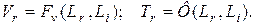 (4.129)
(4.129)
На основании безразмерных уравнений (4.125)-(4.129) можно заключить, что решение рассматриваемой задачи может быть представлено в виде:
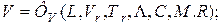
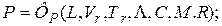 (4.130)
(4.130)
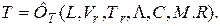
Так как подобие двух систем означает тождество полей безразмерных переменных, то для осуществления подобия необходимо:
в сходственных точках рассматриваемых систем, т.е.
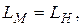 (4.131)
(4.131)
иметь тождественно одинаковое распределение критериев V и Т на границах рассматриваемых систем, т.е.
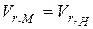 или
или 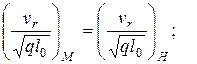
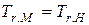 или
или 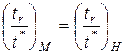 , (4.132)
, (4.132)
и чтобы безразмерные характеристические параметры сравниваемых систем были также одинаковыми, т.е.
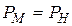 или
или 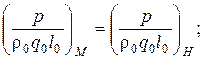
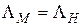 или
или 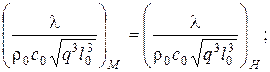
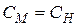 или
или 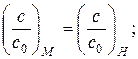 (4.133)
(4.133)
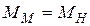 или
или 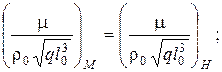
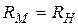 или
или 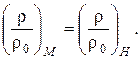
Дата добавления: 2017-10-04; просмотров: 1312;











