Вязкостный режим течения.

Вязкостный режим течения характеризуется исчезающе малым влиянием инерционных сил по сравнению с силами трения и давления. В этом случае на основании анализа уравнений:

движения

;

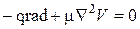сплошности

;

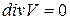граничных условий

,

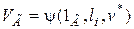где 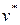– параметрическое значение скорости,

получается одно уравнение связи

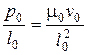, (4.115)

на основании которого устанавливается подобие двух потоков.

Для осуществления подобия необходимо выполнить равенство критериев 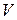на границах потоков в модели и в образце, т.е.

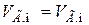или .

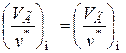Отсюда видно, что подобие может быть осуществлено независимо от размеров модели.

Инерционный режим течения. В этом случае влиянием сил трения, ввиду их малости по сравнению с силами давления и инерции, на режим течения можно пренебречь.

Тогда после приведения уравнений:

движения

;

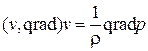сплошности

;

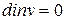граничных условий

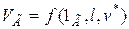
и безразмерному виду получим уравнение связи

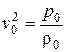. (4.116)

Следовательно, для установления подобия между двумя потоками необходимо выполнить то же условие, что и при вязкостном режиме, т.е.

.

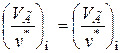В данном случае подобие может быть осуществлено, так же как при вязкостном режиме, независимо от размеров модели, которая. разумеется, должна быть геометрически подобна образцу.

Сопоставим условия, необходимые для осуществления подобия в рассматриваемых задачах:

при наличии сил тяжести:

;

;

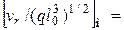
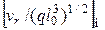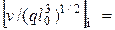
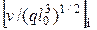при напорном течении

;

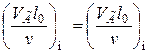при вязкостном течении

;

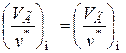при инерционном течении

.

,

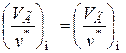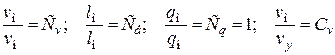получим при наличии влияния сил тяжести

;

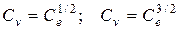при напорном течении

;

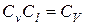при вязкостном и инерционном течении

.

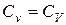Следовательно, для первых двух режимов имеем ограничения в выборе множителей подобия. Действительно, выбрав в первом случае множитель геометрического подобия 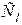, мы тем самым предопределяем множители подобия 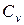и 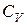. Аналогично и в случае напорного течения.

В противоположность рассмотренным двум первым видам течения, при осуществлении подобия вязкости и инерционного течения мы свободны в выборе множителей подобия. В последних двух случаях подобие обеспечивается одним лишь подобием распределения скоростей. Это свойство инерционного и вязкостного режимов течения называется автомоделью. При этом для вязкостного режима имеет место

,

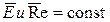а для инерционного режима

.

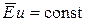Вязкостный режим наблюдается в области малых значений числа 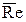, а инерционный – в области больших значений числа 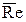. В соответствии с этим принято говорить о первой и второй автомодельных областях. Значение автомодельности для практики моделирования совершенно очевидно, так как оно позволяет осуществить подобие на модели любых размеров с использованием любой рабочей жидкости.