ЗАДАЧИ АНАЛИЗА И СИНТЕЗА. АЛГОРИТМИЧЕСКАЯ СЛОЖНОСТЬ

Одной из основных проблем исследования сложных систем является проблема их анализа и синтеза. Формулировка задач, определение ограничений и выбор целевой функции, разработка аналитических, эвристических и имитационных моделей решения — таковы основные этапы исследования задач анализа и синтеза сложных систем вообще и сетей связи в частности. Как правило, автономное рассмотрение задач анализа и синтеза при всей своей теоретической привлекательности не представляет практического интереса. Через синтез к анализу и через анализ к синтезу - такой должна быть траектория проектирования системы связи.

Для коммутируемых сетей связи задачи анализа и синтеза формулируются следующим образом.

Анализ сети.Заданы сеть G(V,U), т.е. расположение узлов V и характер U их взаимосвязи, число каналов в линиях сети и их пропускная способность; известны вероятности отказов узлов и каналов сети, а также известны помехи и стоимостные показатели элементов. Кроме того, заданы поступающая в сеть нагрузка Y 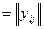, вид потока 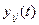информации и категоричность известна средняя длина сообщения или средняя продолжительность телефонного занятия. Известна иерархия сети и зоны обслуживания. Задан алгоритм θ обслуживания; определен алгоритм В (i, j) выбора пути передачи информации между узлами i,j; заданы способ ограничения нагрузки и правило введения резервных узлов и каналов сети связи.

Основная задача анализа сети состоит в расчете параметров cети в целом, параметров отдельных ее фрагментов (например, он) и, наконец, параметров ее элементов; аналогичные задачи возникают при учете возможности аварийного исключения 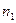, узлов, 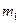линий для оценки живучести сети или без учета аварийных ситуаций для оценки надежности сети.

Синтез сети.Предполагаются известными все данные о поступающей в сеть нагрузке Y 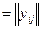известны помехи, характеристики надежности и пропускная способность имеющихся в: распоряжении проектировщика узлов и каналов. 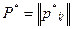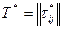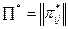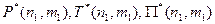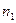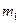Задаются требования на такие показатели синтезируемой сети, как потери (для телефонных сетей), задержки (для сетей с коммутацией сообщений), помехоустойчивость и соответствующие требования ; для случая одновременного аварийного выхода из строя узлов линий связи.

Задача синтеза сети связи состоит в выборе структуры сети, т.е. топологии взаимосвязи узлов сети, пропускной способности линий связи и узлов коммутации, выборе организации θ и определении, если потребуется, иерархии сети и зон обслуживания. Спроектированная сеть связи должна удовлетворять предъявленным требованиям и иметь ограниченную или минимальную стоимость.

При решении задачи синтеза традиционны ограничения на, конфигурацию каналов, накладываемые структурой первичной сети, на допустимое число транзитов, на число непересекающихся по узлам или линиям связи путей между каждой парой узлов; синтезируемой сети и т.д.

Аналитическая сложность проблем анализа и синтеза.Сеть связи можно рассматривать как сложную систему массового обслуживания, и методы теории массового обслуживания применимы при исследовании сетей. В большинстве работ по теории Массового обслуживания анализ систем ограничивается случаем. Простейших схем с однократным обслуживанием (одной фазой; обслуживания). Причина подобного ограничения заключается в том, что анализ потоков в сетях связи методами теории массового обслуживания корректен лишь для пуассоновского или рекуррентного потока заявок, а так как после однократного обслуживания поток существенно отличается от указанных, формальное повторение схемы анализа к обслуживанию заявок на следующих этапах обслуживания невозможно (корректные способы расчета предложены лишь для специальных схем обслуживания [19]).

Основными причинами, существенно затрудняющими а сети, являются взаимозависимость потоков в сети, сложный характер зависимости пропускной способности линии связи от емкости, объема и характера нагрузки, поступающей в линию, также то, что в общем случае стоимость линии является нелинейной функцией как емкости линий, так и ее длины. Сложность тематической модели сети делает невозможным точный аналитический анализ одновременно протекающих взаимосвязанных процессов в сети, таких, как:

-поступление в сеть требований на передачу информации от одного абонента сети к другому;

-установление пути, т.е. поиск путей передачи информации последующей коммутацией каналов или сообщений;

-отказы и восстановления элементов сети;

-освобождение каналов, занятых соединением, время которых истекло, а как следствие отказа пучка каналов прерывание всех соединений, проходящих через отказавшие каналы;

-процессы управления и т. д.

Для получения точного аналитического решения задач анализа и синтеза необходимо фиксировать многие переменные, например фиксировать алгоритм B(I,j) выбора пути. Поскольку аналитические решения проблем анализа и синтеза в своей полной постановке в настоящее время недостижимы, в практике анализа и синтеза сетей связи применяются приближенные аналитические (эвристические) методы исследования или имитационные (статистические) модели либо их сочетание, причем приближенные методы часто основываются на некоторых асимптотических результатах. Метод имитационного моделирования процессов функционирования сетей связи является действенным, а иногда и единственно возможным способом их исследования. Моделирование на ЭВМ позволяет принять или отклонить упрощающие предположения, что дает возможность переходить к новым моделям и к более точным аналитическим исследованиям.

Рассмотрим, например, модель [30] сети с коммутацией сообщений: сеть G(V,U) является сетью очередей 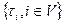. Организация очередей обусловливается структурой приоритетов нагрузки Y 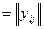, промежутки времени между поступлениями сообщений и длины сообщений распределены экспоненциально c известными средними, узлы сети абсолютно надежны, память узлов неограниченна. помехи отсутствуют; алгоритм B(i,j) выбора пути является, вообще говоря, статическим.

Для представленной модели не существует возможности аналитического исследованиязависимости средней задержки сообщений Т от структуры сети G(V,U), от канальных емкостей 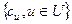[при ∑ c(u)=c=const], от алгоритма выбора пути В(i,j) и от нагрузки 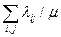,. Здесь 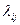- интенсивность требований на передачу сообщений от узла i к узлу j, 1/μ - средняя длина сообщений. Однако гипотеза независимости [30], подтвержденная результатами моделирования [102], позволила получить приведенные в § 3.4 формулы приближенного расчета такой сети.

Для сетей с коммутацией каналов при применении динамических методов выбора B(i,j) в общем случае не существует аналитических методов расчета потерь или задержек и только статистическое моделирование дает возможность получения необходимых характеристик— числа заявок, получивших отказ, числа прерванных соединений, числа транзитов (для всех пар узлов или для некоторых выделенных, например, по признаку высшего приоритета), статистики блокировок по каждой ветви 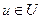и т.д.

Задача синтеза, как правило, связана с просчетом ряда вариантов сети. Она объемнее задачи анализа, и роль статистического моделирования при синтезе сети особенно велика. Решению задач анализа и синтеза сетей связи большой размерности, как правило, предшествует разбиение сети на отдельные подсети, что вызывает необходимость в разработке приемов эффективного разбиения.

АНАЛИЗ

В соответствии с общей схемой задачи анализа сети связи предполагаются заданными структура сети G(V,U), характер потоков нагрузки (заявок на обслуживание) Y 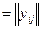и алгоритм обслуживания θ. Результатом решения задачи анализа должны являться параметры качества обслуживания, надежностные и структурные параметры сети.

Расчет параметров качества обслуживания (потерь и задержек).В совокупность задач анализа сетей связи входят, в частности, задачи расчета потерь на пучках каналов (ветвях) и узлах коммутации (потери, вносимые коммутационной системой узла), задачи расчета дифференциальных потерь 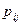между источником i и потребителем j и интегральных потерь Р в сети. Расчеты потерь на пучках каналов и узлах коммутации проводятся методами теории телетрафика [39, 76, 78] с привлечением статистического моделирования, так как практическая сложность исследуемых структур затрудняет их точное аналитическое исследование.

Полнодоступный пучок из t(u) каналов может рассматриваться как простейшая система коммутации. Поступающая на пучок нагрузка y_u(t) [вызовы, требующие занятия свободного канала на некоторое случайное время] при рассмотрении системы (пучка) с потерями делится на обслуженную нагрузку [вызовы, заставшие в момент поступления в систему свободным хотя бы один из t(u) каналов пучка, обслуживаются системой] и потерянную нагрузку (вызовы, не заставшие в момент поступления в систему ни одного свободного канала, покидают систему). Система, в кото­рой вызовы, поступившие в момент занятости всех t(u) каналов не покидают системы, а ожидают освобождения канала называется системой (пучком) с ожиданием. |

Согласно теории телетрафика предполагается, что поток выя зовов является пуассоновским процессом с параметром λ - средним числом вызовов в единицу времени; вероятность поступления k вызовов за время t равна 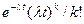и длительность обслуживания одного вызова подчиняется экспоненциальному закону со средним значением 1/μ (для случайного времени 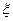обслуживания 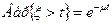) Вероятность 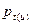занятия ровно k каналов в полнодоступном пучке мощностью t(u) при поступлении на этот пучок простейшего потока с параметром λ определяется формулой Эрланга и обозначается через

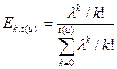. (2.1)

Здесь за единицу времени принимается средняя длительность 1/υ занятия канала. Если λ обозначает среднее число сообщений в произвольную единицу времени, то в (2.1) взамен а подставляется величина y = λ/υ, называемая поступающей нагрузкой.

Из (2.1) следует, что при заданном качестве обслуживания (вероятности потерь 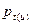) при увеличении числа t(u) каналов в пучке пропускная способность полнодоступного пучка увеличивается; число необходимых каналов обратно пропорционально величине допустимых потерь и при фиксированном числе каналов увеличение допустимых потерь увеличивает обслуженную нагрузку. Заметим, что для практических расчетов параметров качества обслуживания широко используются табличные представления формулы Эрланга для полнодоступного пучка с потерями [2].

Методами теории телетрафика могут быть рассчитаны вероятности потерь в любой коммутационной схеме с потерями. Однако их использование в этом случае гораздо сложнее, чем для случая полнодоступного пучка, в связи с чем для приближенного расчета многокаскадных схем коммутации применяются, как правило, формулы Якобеуса [78].

Рассмотрим некоторые методы расчета дифференциальных 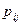и интегральных Р потерь в сети связи.

Расчет потерь для некоммутируемой сети, когда каждому потоку телефонных сообщений 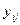от узла i к узлу j предоставляется индивидуальная совокупность 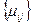путей и каналы этих путей используются только для данного потока 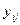, производится довольно просто [34]; гораздо сложнее обстоит дело в случае коммутируемой сети связи с возможностью выбора обходных путей передачи информации.

Одной из основных проблем расчета коммутируемых сетей связи является определение характеристик пропущенной (обслуженной) и потерянной нагрузки на группе путей. При расчете коммутируемой сети характер нагрузки, потерянной на первичной группе путей (избыточной нагрузки), приближенно описывается ее математическим ожиданием и дисперсией

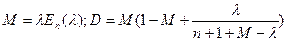, (2.2)

полученными Риорданом [132] и использованными Вилкинсоном |141] для вычисления нагрузки на сетях с обходами (допущения метода эквивалентных замен [141] представлены в § 1.2). Исходные нагрузки при этом предполагаются пуассоновскими. Предполагается также, что пуассоновский характер потоков сохраняется как для потерянной, так и для пропущенной нагрузки, что, однако, не влияет на схему расчета потерь, так как расчет по среднему [формула (2.1)] может быть заменен расчетом по двум параметрам в соответствии с методом [141].

В настоящее время существует ряд методов расчета потерь в сетях коммутации каналов. Метод, приведенный в [115] без доказательства его сходимости, предполагает поиск путей установления соединения без возвращения в уже пройденные узлы. Итеративные процедуры расчета в [7, 46] доведены до программной реализации, причем итерации повторяются до тех пор, пока для каждой ветви вероятности потерь, вычисленные в двух последующих итерациях, будут отличаться менее чем на зара­нее заданное число е. Алгоритм [18] основан на принципе после­довательного нагружения сети входными потоками.

Методы расчета временных задержек — основного параметра сетей передачи дискретной информации — основаны на теории очередей для единственной станции обслуживания. Как уже отмечалось, анализ очередей затруднен тем, что потоки в сетях взаимозависимы. Подсчет средней задержки в передаче сообщения производится в предположении [30], что возникновение сообщений в узлах сети распределено по пуассоновскому закону, длина определенного сообщения, передаваемого от узла к узлу,—независимая случайная величина, подчиняющаяся экспоненциальному распределению, процессы в узлах сети независимы, а емкость памяти в узлах сети неограничена.

При этих предположениях средняя задержка Т вычисляется по формуле

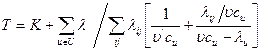, (2.3)

где λu — интенсивность нагрузки на ветви 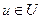; 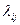— интенсивность входного потока 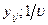— средняя длина сообщений в сети; 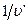— средняя длина сообщений, поступающих в сеть; с_и — пропускная способность линии 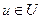/; К— константа, соответствующая времени обработки сообщений в узлах; t_u— задержка распространения сигнала в линии 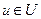. Расчет Т основан на расчете 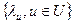и для сетей со структурой дерева или в случае единственности пути 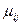для каждой пары узлов (i, j) не слишком затруднителен.

Расчет структурных параметрови показателей надежностиНеобходимость расчета структурных параметров и показателей надежности сети связи вызывается следующими основными причинами: необходимостью оценки промежуточных вариантов сети на этапе ее синтеза и необходимостью оценки состояния сети для принятия решения по управлению сетью в условиях поражения элементов сети.

Так как вычисление структурных параметров графовых мо­делей G(V, U), G(У) и G(θ) (см.гл.1) представляет довольно простую процедуру и не вызывает принципиальных затруднений [определение диаметра d графа G может производиться по алгоритму [69], трудоемкость вычислений по которому оценивается в О (n³)* операций, где n — число вершин анализируемого графа G], то имеет смысл остановиться лишь на вопросах определения показателей надежности сети.

Отметим некоторые теоретические результаты, которые могут оказаться полезными при расчете показателей надежности сети связи. Будем считать граф G w-связным (λ-связным), если его вершинная (реберная) связность равна w(G)(λ(G)). Представляют интерес следующие теоремы:

Теорема Уитни (а) [140]: граф G w-связан тогда и только тогда, когда любая пара его вершин соединена, по крайней мере, w путями, попарно не имеющими общих вершин.

Теорема Менгера [123]: граф G λ -связан тогда и только тогда, когда любая пара его вершин соединена, по крайней мере, λ путями, попарно не имеющими общих ребер.

Теорема Харари [64]: в каждом графе G(V, U) наибольшее число попарно вершинно - непересекающихся разрезов, разделяющих две вершины i, j 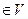, равно p(i, j) — 1, где ρ(i, j) — число ребер в кратчайшем по числу ребер пути в графе G(V, U) между вершинами i,j.

Теорема Фалкерсона [105]: в каждом графе G (V, U) наибольшее число попарно реберно - непересекаюшихся разрезов, разделяющих две вершины i, j 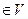, равно p(i, j)

Теорема Уитни (б) [140]: в каждом графе G

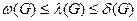, (2.4)

* Если f(n) точное выражение для трудоемкости вычислений, то 0{g(n)) означает, что 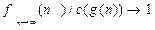, где с — некоторая константа.

Kmg

где δ — минимальная степень вершины графа G (под степенью вершины понимается число инцидентных ей ребер).

Из (2.4) следует, что более критической является вершинная связность графа, в связи с чем целесообразно использовать характеристику ω(G) в качестве рабочего параметра при решении задач синтеза сети с определенными значениями связности.

Вопросы расчета параметров ω(λ) графа G - определение вершинной (реберной) связности графа G - были решены в [104, 69] соответственно, причем было показано, что трудоемкость алгоритма определения λ(G) не превышает О (n³) операций, где n - число вершин графа G, и значительно превосходит трудоемкость алгоритма определения ω(G).

Представляются целесообразными следующие методы анализа связности сети связи:

метод Мура - Шеннона [45] вычисления вероятности нарушения связности сети по формуле

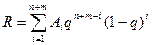, (2.5)

где R - вероятность нарушения связности сети; 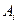- число подсетей, содержащих i элементов (узлов и ветвей сети); q - вероятность отказа элемента; n - число узлов сети; т - число ветвей сети (следует отметить ограниченность применения метода [45], вызываемую некорректностью предположения о равной надежности узлов и ветвей сети и невозможностью аналитического вычисления Аi для больших сетей);

рекуррентный метод [11З] вычисления вероятности, нарушения связности пары узлов сети, основанный на алгоритме декомпозиции графа сети и позволяющий учесть надежность каждого элемента сети (метод применим лишь к небольшим сетям);

логико-вероятностный метод [103] расчета вероятности связности пары уз­лов сети, основанный на применении булевых функций для описания структуры графа сети в предположении абсолютной надежности узлов сети;

метод [80] расчета вероятности связности пары узлов сети с учетом надежности узлов;

метод [93] расчета вероятности связности нары узлов сети с учетом надежности ребер;

метод [129] расчета различных критериев надежности сети путем декомпозиции ее на подсети; метод достаточно эффективен для сравнительно малосвязных сетей.

В общем случае анализ показателей надежности больших распределенных (оценка параметров централизованной сети является тривиальной процедурой) сетей связан с огромным объемом вычислений. Действительно, если рассмотреть модель ненадежной сети как случайный граф (G, X), то

Вер((G,X)обладает свойством φ)= 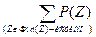(2.6)

где Z - подграф графа G; Ф - множество всех подграфов графа G; Р(Z) - вероятность существования подграфа Z, причем анализ сети требует, как правило, перебора порядка 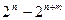вариантов (n - число вершин; m - число ребер сети) состояний ненадежной сети.

В связи с этим наиболее целесообразным приемом анализа: параметров надежности сети связи представляется сочетание аналитических оценок со статистическим моделированием по методу Монте-Карло (применимость метода Монте-Карло обусловливается простотой структуры вычислительного алгоритма).

Методом статистического моделирования целесообразно оценивать, например математическое ожидание числа n(p) (p - вероятность выхода из строя элементов сети) пар узлов сети, между которыми невозможно установление соединения [138]. Заметим, что использовать аналитические выражения для подсчета n(p) при большихnпрактически не удается.

Многие показатели надежности, такие, например, как вероятность связности и средний размер компоненты графа сети, взаимосвязаны, хотя аналитический характер этой зависимости не выяснен до конца. Тем не менее результаты исследований в области случайных графов дают ряд полезных оценок надежности, например аналитических оценок вероятности связности произвольного случайного графа.

Нижняя оценка вероятности связности [42]

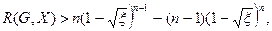(2.7)

где -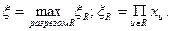

В случае, когда x_u = q, для каждого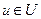

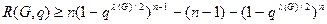(2.8)

где, как и ранее, λ(G) - реберная связность графа G(V, U). Верхние оценки вероятности связности [41]

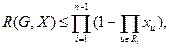(2.9)

где 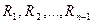— базис разрезов (т.е. для каждой пары i, 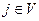существует 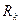, разделяющий i,j); в случае x_u=q для каждого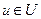

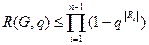(2.10)

и

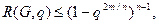(2.11)

где 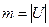, причем исследования показали, что верхняя оценка (2.9) практически совпадает с вероятностью связности.

Существует [40] оценка R(G, X) вероятности связности произвольного случайного графа через вероятность связности полного графа, причем представленные выше оценки таковы, что для сетей с числом ветвей, примерно равным 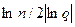, они совпадают (асимптоти-чески) с вероятностью связности.

Вероятность парной связности оценивается следующим образом:

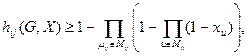(2.12)

где 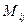- некоторая совокупность путей от i к j без общих ребер;

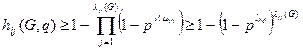, (2.13)

где 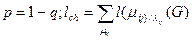- средняя длина пути.

СИНТЕЗ

В соответствии с общей схемой задачи синтеза сетей cвязи будем предполагать заданными характер потоков нагрузки (2.7) 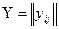, нормы качества обслуживания и принятые ограничения

на структурные параметры сети. Результатом решения задачи синтеза является выбор структуры G (V,U) сети связи и законов управления θ сетью связи, обеспечивающих значения показателей качества обслуживания в пределах заданных норм обслуживания при минимизации общественных затрат.

В общем случае синтез сетей связи может производиться по различным критериям (см., например, [18, 24. 53, 54, 60]). К их числу относятся:

а) стоимостные критерии сети связи: затраты на реализацию сети в целом, канальную емкость сети, затраты нa канало - километр сети, на стоимость передачи единицы информации по сети и т. д.;

б) надежностные критерии сети связи;

в) структурные критерии сети связи: суммарная длина линий, число канало - километров, число транзитов (среднее или максимальное и т. д.);

г) критерии качества обслуживания в сети связи;

д) обобщенные критерии сети связи: эффективность сети как отношение переданного количества информации к экономическим затратам на сеть, эффективность сети как математическое ожидание величины пропущенной (обслуженной) сетью нагрузки, критерии потерь (экономических убытков из-за неполучения информации или дополнительных затрат на восстановление или ремонт технических средств сети) в зависимости от надежности, т.е. критерий средних потерь или вероятность превышения потерями заданной нормы, количество информации, передаваемой в сети за установленное время с заданной вероятностью доставки, и т. д.

Как правило, в задачах синтеза сетей связи используются стоимостные критерии, а надежностные и структурные характеристики выступают в качестве дисциплинирующих (ограничивающих) факторов. В случае синтеза вторичной коммутируемой сети связи путем аренды каналов первичной сети в качестве стоимостного критерия обычно используется плата за арендуемые каналы, определяемая выражением

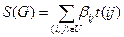, (2.14)

аналогичным выражению (1.30), где t(ij) — емкость пучка каналов (ij), a 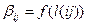- неубывающая ступенчатая функция; (при синтезе первичной сети учитываются приведенные затраты как на линии связи, так и на узлы коммутации).

Значительное число работ, посвященных вопросам синтеза сетей связи, используют в качестве критерия те или иные показатели надежности сети. Рассмотрим некоторые результаты, полученные при таком подходе к решению задачи синтеза.

При синтезе 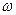-связного графа сети G(V, U) возможны следующие постановки задачи: ;

1.По заданным n=\V\, m=\U\ и одинаковой стоимости (длине) ребер построить граф G(V,U) с максимальным значением 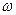(G (V,U)).

2.По заданной матрице избыточности 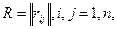где 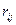- целое положительное число, построить граф G(V,U) с минимальным числом ребер U таким образом, чтобы для каждой пары вершин s, 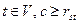,где 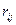- число попарно независимых по вершинам путей между s, t в графе G(V,U).

В постановке 1 алгоритмы решения задачи для ориентированных и неориентированных сетей представлены соответственно в [82, 85]. Задача в постановке 2 не решена даже для случая неориентированного графа G(V,U), так же как не решена задача в постановке 1 для случая неодинаковой стоимости ребер.

При синтезе λ - связного графа сети G(V,U) возможны постановки задач, аналогичные постановкам задач для случая синтеза 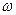- связных структур. Для одинаковой стоимости ребер задача максимизации реберной связности заключается в построении сети G(V,U) с т ребрами и п вершинами, для которой λ{G{F, U)) = [2т/п]. Она решена в [96]. В [99] решается задача построения по заданной матрице избыточности 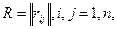где 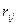- целые положительные числа графа G(F,U) с минимальным числом ребер U, такого, что для каждой пары вершин s. 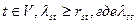- число попарно независимых по ребрам путей в графе G(V,U).

Проблема синтеза сетей с неодинаковой стоимостью ребер по критерию реберной связанности исследована еще недостаточно. Отметим лишь эвристический алгоритм [136] построения сети минимальной стоимости по заданной матрице избыточности R и алгоритм синтеза сети связи, обеспечивающей существование не менее двух независимых путей между каждой парой узлов сети (узлы разбиваются на группы — число узлов в группе равно числу групп, внутри группы узлы связываются по принципу «каждый с каждым» и каждый узел группы связан, по крайней: мере, с одним узлом другой группы).

Одной из разумных оценок надежности сети связи может служить наибольшая из вероятностей нарушения связи между различными парами узлов. Пусть вероятность разрыва всех путей: между i-м и j-м узлами сети равна p(i,j). Используя р = 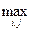p (i,j) как меру надежности сети, в [142] предлагается эвристическая процедура решения задачи синтеза сети путем построения максимально связного графа сети, т. е. графа, для каждой пары i, j вершин которого мощность наименьшего из разрезов, разделяющего эти узлы, равна минимальной из степеней вершин i, j.

Дальнейшее обсуждение вопросов надежности сети будет проводиться при рассмотрении методов синтеза распределенных сетей. Отметим только, что вид оптимальной структуры синтезируемой сети зависит, вообще говоря, от значений вероятностей отказа ее элементов.

Схема синтеза сети связи включает в себя выбор топологии сети с заданными структурными и надежностными характеристиками и определение пропускных способностей линий связи. Как правило, при расчете топологии сети связи проектировщик задается некоторой исходной сетью, например некоторым деревом, сетью с определенной связностью (реберной, вершинной или смешанной) и с минимальным числом ветвей, полной сетью, несвязной сетью и т. д. (возможен учет различных топологических ограничений).

Исходная сеть может быть заведомо избыточной, удовлетворять или не удовлетворять критериям синтеза. К исходной сети применяют различные методы «локальной» оптимизации, в том числе и итеративные методы [63], производя целенаправленный перебор возможных структур, получаемых из исходной сети путем локальных изменений. Процесс синтеза заканчивается построением «локально оптимальной» сети, которая, вообще говоря, зависит как от исходной сети, так и от правил «локальных» воздействий и порядка их проведения.

Примером такого подхода к решению задачи синтеза сети является алгоритм [101]. Исходной сетью алгоритма является некоторое дерево Т. Пусть u - ребро вне дерева Т, а u'- ребро, принадлежащее единственной цепи по дереву Т относительно вершин — концов ребра u. Граф Т\u'+и так же является деревом. С помощью ряда аналогичных операций из дерева Т можно получить любое другое дерево, возможно даже выписать без повторений все деревья графа. |

По алгоритму [101] в исходном дереве Т выбирается некоторая (произвольная) вершина 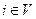(V- множество вершин Т) и определяется вершина 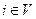, ближайшая к вершине i, но не соединенная с ней. Исследуется сеть Т+(ij) перебором деревьев, полученных из T+(ij) удалением ребер (по одному ребру) единственного в Т+(ij) цикла. Для каждого дерева применяется алгоритм оптимального выбора пропускной способности ветвей и определяется стоимость сети. Для деревьев, стоимость которых меньше стоимости Т, алгоритм замены применяется вновь и т. д. до получения оптимальной (в указанном смысле) сети.

Процедура [101] является одной из возможных эвристических процедур локальной оптимизации проектирования централизованных сетей связи. Здесь и в дальнейшем под централизованной сетью понимается сеть-дерево, каждая пара узлов которой может быть соединена единственным путем; распределенная сеть отличается от централизованной наличием дополнительных путей передачи информации (рис. 2.1, 2.2).

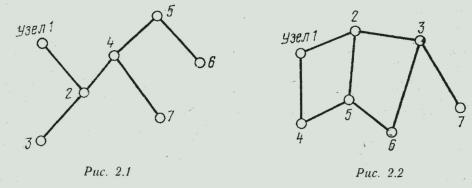
Одним из основных вопросов проектирования централизованных сетей является определение топологии сети, минимальной по стоимости. Поскольку централизованная сеть есть дерево, представляется целесообразным выбор в.качестве исходной структуры для последующего этапа локальной оптимизации кратчайшего связывающего дерева Прима [53] или минимального дерева Штейнера [14]. Дерево Прима на множестве п вершин при заданной матрице расстояний (весов) между каждой парой вершин обладает тем свойством, что среди всех возможных деревьев на заданных п вершинах оно соответствует дереву с минимальной суммой весов ребер. Задача минимизации суммы чисел (весов) может быть расширена до общей задачи минимизации любой возрастающей симметрической (значение функции инвариантно относительно перестановок значения переменных) или максимизации любой убывающей симметрической функции весов ребер дерева, т. е. кратчайшее связывающее дерево Прима минимизирует все возрастающие и максимизирует все убывающие симметрические функции весов ребер. Так, например, минимизация (1- 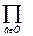(1- q_u)), где q_u - вероятность отказа ребра u, 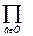(1- q_u)—вероятность связности дерева Т, достигается тем же деревом, которое минимизирует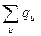

В некоторых случаях сумма весов ребер дерева может быть уменьшена, если в дополнение к его п вершинам ввести добавочные m вершин (точек Штейнера) и строить кратчайшее дерево на п+m вершинах (дерево Штейнера). При этом сумма весов в минимальном дереве Штейнера, определяемом оптимальным число добавочных вершин и их местоположением, всегда не больше суммы весов в дереве Прима. В техническом плане к задаче построения минимального дерева Штейнера сводится задача выбора числа и места расположения концентраторов (при учете топологии сети терминалов). В связи с этим представляет интерес поиск приближенных методов решения задачи Штейнера.

Несмотря на очевидную привлекательность топологии Прима и Штейнера, к общем случае выбор структуры сети из класса деревьев может и не привести к оптимальной по стоимости сети. Оптимальное решение является деревом только при представлении стоимостей всех ветвей как выпуклых функций их пропускных способностей. На практике, однако, стоимости ветвей не являются выпуклыми функциями их пропускных способностей, что приводит к возможности построения распределенной сети, более экономичной по сравнению с любым деревом.

Как правило, централизованная сеть строится по иерархическому принципу. В типичной структуре трехуровневой централизованной сети (рис. 2.3) высший уровень иерархии — центральный

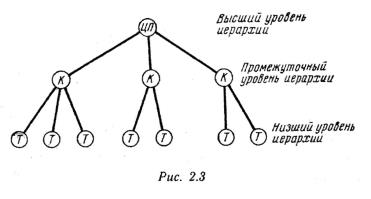
процессор (ЦП)—связан с низшим уровнем — терминалами (Т) через промежуточный уровень иерархии — концентраторы (К).

В [86] рассматривается задача выбора числа концентраторов, их размещения и распределения терминалов по концентраторам при минимизации суммарной стоимости соединений концентраторов с терминалами в классе деревобразных радиальных структур (рис 2.3). Поставленная задача может быть решена методом целочисленного линейного программирования. Так как время решения при этом экспоненциально зависит от размерности решаемой задачи, вследствие чего точное ее решение является недостижимым в практически интересных случаях, то оправданы поиски эвристических алгоритмов, примерами которых являются программы ADD[119], DROP[97J, ATD[144], СОМ[121], LRC[94].

Алгоритмы ADD, DROP и LRC работают в классе звездных графов — сетях непосредственной связи терминалов и концентратора (рис. 2.4). Так как звездный граф является дорогостоящей структурой, обладающей, правда, хорошими; характеристиками использования каналов, представляет интерес поиск более экономичных способов построения сети связи терминалов с концентратором.