Лекция № 5. Метод молекулярных орбиталей
Метод МО рассматривает молекулу как единое образование, в котором каждый электрон принадлежит частице и движется по молекулярным орбиталям в поле всех ядер и остальных электронов молекулы. Молекулярная орбиталь - это область пространства в молекуле, вероятность нахождения электрона в которой существенно отличается от нуля. В отличие от атомной орбитали (АО), молекулярная орбиталь (МО) многоцентрова и охватывает несколько ядер. Заполнение молекулярных орбиталей электронами происходит в порядке увеличения их энергии с соблюдением принципа запрета Паули и правила Гунда. Волновая функция МО (y) конструируется как линейная комбинация волновых функций АО (ji):
y = 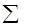 сiji
сiji
АО, пригодные для составления МО, должны иметь близкую энергию, одинаковую симметрию и перекрываться в заметной степени. При этом число полученных МО равно числу исходных АО.
Различают три типа молекулярных орбиталей: связывающие, разрыхляющие (антисвязывающие) и несвязывающие. Связывающие МО имеют энергию, меньшую по сравнению с исходными атомными орбиталями. Их заполнение стабилизирует молекулу. Разрыхляющие молекулярные орбитали имеют энергию более высокую по отношению к исходным АО. Заполнение электронами разрыхляющих МО ведет к дестабилизации частицы. Несвязывающие МО локализованы на отдельных атомах и фактически представляют собой атомные орбитали, перенесенные в молекулу без изменения. По симметрии МО разделяют на s (симметричные относительно линии связи) и p (антисимметричные относительно линии связи). Последние меняют знак волновой функции при повороте вокруг линии связи.
Рассмотрим электронное строение двухатомных молекул, образованных элементами первого периода. В качестве базисного набора АО будем использовать 1s-орбитали, линейные комбинации волновых функций которых дадут y-функции двух молекулярных орбиталей:
y1 = с1j1sA + c2j1sB ; y2 = с3j1sA - c4j1sB
Форма граничной поверхности полученных МО и энергетическая диаграмма молекулы имеют следующий вид:
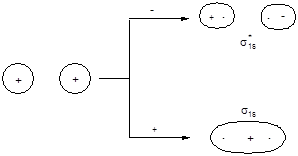
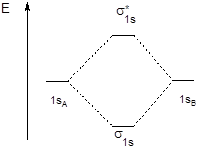
АО МО
Разместив на МО электроны, получим электронные формулы соответствующих молекулярных частиц. Для качественной характеристики устойчивости молекул в методе МО используется кратность связи (КС), которую рассчитывают как половину разности числа связывающих и разрыхляющих электронов. Кратность связи увеличивается при увеличении устойчивости молекулы. Частицы, для которых КС £ 0, не существуют.
| Частица | Электронная формула | КС | Магнитное поведение |
| H2+ | (s1s)1 | 1/2 | Парамагнетик |
| H2 | (s1s)2 | Диамагнетик | |
| H2- | (s1s)2(s1s*)1 | 1/2 | Парамагнетик |
| He2+ | (s1s)2(s1s*)1 | 1/2 | Парамагнетик |
| He2 | (s1s)2(s1s*)2 | - |
При конструировании МО двухатомных гомоядерных молекул, образованных элементами второго периода, в качестве исходных АО можно использовать 2s- и 2p-орбитали. 1s-Орбитали входят в состав молекулы без изменения, т.е. являются несвязывающими. Схема и результат взаимодействия волновых функций 2s-орбиталей аналогичны рассмотренным выше для s-орбиталей элементов первого периода. 2px-Орбитали, ориентированные по линии связи, взаимодействуют с образованием двух s-МО:
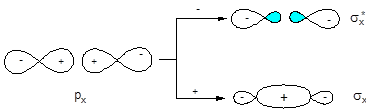
АО МО
Взаимодействие 2p-орбиталей, ориентированных по осям y и z, приводит к образованию двух наборов p-МО (pz, pу):

АО МО
Энергетическая диаграмма молекулярных орбиталей двухатомной молекулы, образованной элементами конца второго периода (начиная с кислорода), имеет вид, представленный на рисунке справа:
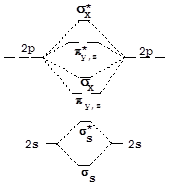
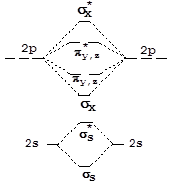
У элементов, расположенных в начале второго периода, близость энергии 2p- и 2s-орбиталей приводит к участию последних в формировании sх-орбиталей и увеличению их энергии. Вследствие этого на энергетической диаграмме уровни sх и py,z меняются местами (левая часть рисунка).
Разместив электроны на МО в порядке возрастания их энергии, получим электронные формулы соответствующих молекулярных частиц.
| Частица | Электронная формула | КС | Магнитное поведение | |||||
| Li2 | KK(ss)2 | Д | ||||||
| Be2 | KK(ss)2(ss*)2 | - | ||||||
| B2 | KK(ss)2(ss*)2(py)1(pz)1 | П | ||||||
| C2 | KK(ss)2(ss*)2(py)2(pz)2 | Д | ||||||
| N2 | KK(ss)2(ss*)2(py)2(pz)2(sx)2 | Д | ||||||
| O2+ | KK(ss)2(ss*)2(sx)2(py)2(pz)2(py*)1 | 2,5 | П | |||||
| O2 | KK(ss)2(ss*)2(sx)2(py)2(pz)2(py*)1(pz*)1 | П | ||||||
| O2- | KK(ss)2(ss*)2(sx)2(py)2(pz)2(py*)2(pz*)1 | 1,5 | П | |||||
| F2 | KK(ss)2(ss*)2(sx)2(py)2(pz)2(py*)2(pz*)2 | Д | ||||||
| Ne2 | KK(ss)2(ss*)2(sx)2(py)2(pz)2(py*)2(pz*)2(sx*)2 | - | ||||||
Из полученных данных видно, что метод МО более адекватно отражает физические свойства молекул, в частности, он объясняет парамагнетизм молекулы кислорода. Кроме этого метод молекулярных орбиталей позволяет описать как одноэлектронные, так и делокализованные связи. Однако он несколько проигрывает методу валентных схем в наглядности.
Литература: [1] с. 135 - 143; [2] с. 118 - 126; [3] с. 52 - 63
Лекция № 6. Ионная связь. Металлическая связь, зонная теория кристаллов.
Водородная связь. Межмолекулярное взаимодействие, силы Ван-дер-Ваальса.
Агрегатное состояние вещества
Ионной называется связь, обусловленная электростатическим притяжением разноименно заряженных ионов. При этом ионы могут быть как молекулярными, например, в нитрате аммония - NH4+NO3-, так и атомными, например, в хлориде натрия - Na+Cl- . К образованию ионной связи с участием атомных частиц способны элементы, сильно отличающиеся по электроотрицательности, например, щелочные металлы и галогены. При этом образование ионной связи подразумевает перенос электронов к атому с большей электроотрицательностью с образованием пары ионов.
Рассмотрим в качестве примера образование ионной связи во фториде лития. Для этого вначале вспомним электронное строение взаимодействующих атомов и оценим их валентные возможности. Атом лития имеет электронную формулу 1s22s1. Очевидно, что для достижения устойчивой структуры ему необходимо отдать один электрон, расположенный на внешнем энергетическом уровне.
Li ® Li+ + e-
1s22s1 ® 1s2 + е-
Атому фтора, который имеет электронную формулу 1s22s22p5, для достижения устойчивой конфигурации электронной оболочки достаточно присоединить один электрон, источником которого является атом лития:
F + e- ® F-
1s22s22p5 + e- ® 1s22s22p6
Электростатическое притяжение образовавшихся ионов и приводит к образованию вещества с ионной связью:
Li + F ® Li+ + F- ® Li+F-
Следует отметить, что описанная картина несколько идеализирована. В реальности полного переноса электрона не происходит, что вызвано поляризующим действием катиона лития, за счет которого он оттягивает на себя часть электронной плотности аниона. Квантово-механический расчет показывает, что в молекуле фторида лития эффективный заряд на атоме лития составляет +0,51, соответственно на атоме фтора -0,51, т.е. связь литий-фтор в значительной мере ковалентна.
Электростатическая природа ионной связи обуславливает ее основные свойства - ненаправленность и ненасыщаемость. Ненаправленность ионной связи обусловлена сферической симметрией электростатического поля иона, вследствие которой заряженная частица притягивает ионы противоположного знака равномерно по всем направлениям.
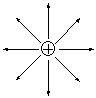
Образование ионной связи с частицей противоположного заряда нарушает сферическую симметрию поля, но само поле не исчезает. Поэтому, образовав одну ионную связь, ион не утрачивает способность к электростатическому взаимодействию с другими частицами.
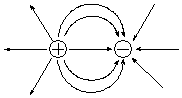
Вследствие этого молекулы с ионным типом связи существуют только при высокой температуре в газовой фазе. В конденсированном состоянии ионы стремятся окружить себя максимальным число ионов противоположного знака, что приводит к образованию веществ с немолекулярной структурой - ионных агрегатов (ионных кристаллов).
Металлической называется химическая связь, обусловленная электростатическим притяжением катионов металла, расположенных в узлах кристаллической решетки, и общего электронного облака (обобщенного электронного газа), охватывающего весь кристалл. Рассмотрим сущность металлической связи на примере лития, имеющего кубическую объемно-центрированную кристаллическую решетку, в которой каждый атом лития окружен восьмью соседями (координационное число восемь).
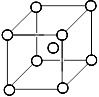
Очевидно, что атом лития не может образовать восемь ковалентных связей, потому что, как элемент второго периода, он имеет только четыре валентные орбитали. Не могут быть связи в кристалле лития и ионными, потому что атомы лития готовы отдать свой единственный электрон, но принять его некому. Поэтому атомы лития отдают валентные электроны в общее пользование, образуя общее электронное облако, охватывающее весь кристалл.
Наличие подвижных электронов обобщенного электронного газа приводит к тому, что металлы имеют ряд общих физических свойств: высокую электропроводность и теплопроводность, характерный металлический блеск и высокую отражающую способность, пластичность и ковкость.
Для количественного описания свойств металлов и других кристаллов в химии твердого тела широко используется формализм зонной теории, которая фактически представляет собой обобщение метода молекулярных орбиталей для большого числа взаимодействующих атомов (порядка числа Авогадро, 6×1023). Согласно методу МО взаимодействие валентных орбиталей большой совокупности атомов приводит к образованию большого числа молекулярных орбиталей, энергетические различия между которыми столь ничтожно малы, что они сливаются в одну энергетическую зону. Для кристаллов, образованных элементами второго периода, взаимодействие 2s- и 2p-орбиталей приводит к образованию двух энергетических зон.
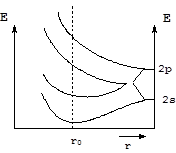
Нижняя зона, в которой расположены электроны, осуществляющие образование химической связи, называется валентной зоной. Электроны, расположенные в этой зоне, у ковалентных и ионных кристаллов локализованы в определенных областях пространства и не способны перемещаться по кристаллу. Верхняя энергетическая зона называется зоной проводимости. Поскольку она вакантна, попадая в нее, электроны могут свободно перемещаться по всему кристаллу, осуществляя проводимость электрического тока. На энергетической диаграмме кристалла существует еще одна область значений энергий, которые электроны принимать не могут - запрещенная зона. Ее ширина обычно и определяет свойства кристалла. Если ширина запрещенной зоны DЕ > 3,0 эВ, то никакими внешними воздействиями электроны не могут быть переведены из валентной зоны в зону проводимости и кристалл является диэлектриком. При ширине запретной зоны в пределах 0,1 - 3,0 эВ возможен перевод части электронов из валентной зоны в зону проводимости под влиянием внешнего воздействия (облучения светом или повышения температуры). Такой кристалл будет полупроводником. И наконец, при ширине запретной зоны меньше 0,1 эВ фактически происходит перекрывание валентной зоны и зоны проводимости и электроны, осуществляющие химическую связь, могут свободно перемещаться по всему кристаллу, который будет обладать электронной проводимостью, т.е. будет проявлять свойства металла.
Водородной связью называется электростатическое взаимодействие атома водорода, связанного с сильно электроотрицательным элементом, с другими атомами. Прочные водородные связи образует атом водорода, связанный с атомом фтора, кислорода или азота. Электроотрицательность других элементов недостаточна для того, чтобы заставить связанный с ними атом водорода образовать водородную связь. Механизм образования водородной связи рассмотрим на примере взаимодействия молекул фтороводорода. Высокая электроотрицательность атома фтора приводит к тому, что связь водород-фтор в данной молекуле сильно полярна и общая пара электронов смещена к фтору H®F. Поскольку у атома водорода отсутствует внутренняя электронная оболочка, оттягивание его валентного электрона почти полностью обнажает ядро, представляющего собой элементарную частицу - протон. По этой причине сильно поляризованный атом водорода обладает очень мощным электростатическим полем, за счет которого он притягивается к атому фтора другой молекулы фтороводорода с образованием водородной связи. Значительный вклад в образование водородной связи вносит донорно-акцепторное взаимодействие "вакантной" 1s-орбитали атома водорода с неподеленной электронной парой атома фтора.
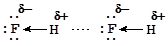
Водородная связь более длинная по сравнению с ковалентной и имеет меньшую энергию (8-40 кДж/моль). Тем не менее, она оказывает очень большое влияние на физические свойства веществ, значительно увеличивая их температуры плавления и кипения. Так, фтороводород имеет т.пл. -83 °С и т.кип. +20 °С , в то время как его ближайший аналог - хлороводород плавится при температуре -114 °С и кипит при -85 °С. Фактически, за счет водородных связей, фтороводород представляет собой полимер, который начинает частично диссоциировать только при температуре, близкой к температуре кипения. Но даже в газовой фазе фтороводород существует в виде малых ассоциатов молекул, в основном, в виде димеров. В виде мономерных молекул фтороводород существует только при температурах выше 90 °С. Очень прочные водородные связи образует молекула воды, окруженная в кристаллическом состоянии (лед) четырьмя соседями:
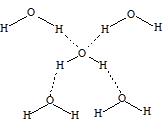
Трехмерная сетка водородных связей, построенная из тетраэдров, существует и в жидкой воде во всем интервале температур от плавления льда и до ее кипения.
Наряду с межмолекулярными существуют и внутримолекулярные водородные связи, не оказывающие столь значительного влияния на физические свойства вещества.
| Внутримолекулярная водородная связь | Межмолекулярная водородная связь |
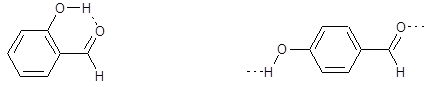
| 2-гидроксибензальдегид, т.пл. –7 °С | 4-гидроксибензальдегид, т.пл. +117 °С |
Силами Ван-дер-Ваальса (силами межмолекулярного взаимодействия) называют силы электростатического взаимодействия диполей вещества. По происхождению диполей выделяют три типа сил межмолекулярного взаимодействия:
1. Ориентационное взаимодействие - электростатическое притяжение постоянных диполей, которые ориентируются друг по отношению к другу противоположными полюсами.
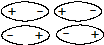
2. Индукционное взаимодействие - электростатическое притяжение постоянного и наведенного (индуцированного) диполя.
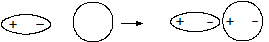
3. Дисперсионное взаимодействие - электростатическое притяжение мгновенных микродиполей вещества. Возникновение мгновенных микродиполей вызвано случайным нарушением симметрии распределения электронной плотности в частице. При проявлении сил дисперсионного взаимодействия мгновенные микродиполи появляются и исчезают синхронно, ориентируясь таким образом, чтобы частицы притягивались.
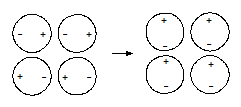
Вклад дисперсионного взаимодействия в энергию межмолекулярного взаимодействия увеличивается при возрастании поляризуемости молекулы. Например, для молекул иодоводорода - HI - энергия дисперсионного взаимодействия (60,47 кДж/моль) составляет 98,5% энергии сил межмолекулярного взаимодействия.
В зависимости от расстояниями между частицами вещества и сил их взаимодействия выделяют четыре основные агрегатные состояния вещества: плазма, газ, жидкость и твердое тело. Последние два состояния называют конденсированными.
Плазма - это состояние ионизированного газа, представляющего собой смесь нейтральных атомов, электронов, ионов и атомных ядер. Различают холодную (10-100 тыс.град.) и горячую (свыше 100 тыс.град.) плазму.
Газообразное состояние вещества характеризуется отсутствием заметного взаимодействия между молекулами, способными свободно перемещаться друг относительно друга. Состояние идеального газа, который можно рассматривать как совокупность материальных точек, описывается уравнением Менделеева-Клапейрона.
рV = nRT,
где р - давление газа (Па), V - его объем (м3), n - количество вещества, R - универсальная газовая постоянная, равная 8,314 Дж/(моль×К).
Состояние реального газа передается уравнением Ван-дер-Ваальса:
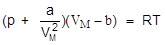
где VM - молярный объем газа, a и b - экспериментальные параметры, учитывающие объем молекул и силы взаимодействия между молекулами.
Жидкое состояние характеризуется наличием ближнего порядка (упорядоченности) в расположении частиц, способных легко перемещаться друг относительно друга. Близким по своим свойствам к жидкому является аморфное состояние, которое характеризуется наличием ближнего порядка в расположении частиц, неспособных свободно перемещаться друг относительно друга.
Аморфное состояние является одной из разновидностей твердого состояния вещества, и может рассматриваться как переохлажденная жидкость, поэтому оно термодинамически нестабильно. Кроме аморфного, для твердых веществ возможно кристаллическое состояние, которое характеризуется наличием дальнего порядка в расположении частиц, неспособных свободно перемещаться друг относительно друга. Отличительной особенностью кристаллического тела является строго определенная форма и анизотропия - зависимость физических свойств вещества от направления в пространстве.
Кристалл - это твердое тело, ограниченное плоскими поверхностями (гранями). Строгость формы кристалла является отражением строгости его внутреннего строения. Идеальный кристалл характеризуется бесконечной пространственной решеткой, состоящей из идентичных элементарных ячеек. Существует 14 типов кристаллических решеток (решеток Бравэ), принадлежащих семи кристаллографическим системам (сингониям), которые отличаются соотношением параметров элементарной ячейки. Последние не обязательно совпадают с прямоугольной системой координат.
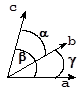
Наиболее высокосимметричной является кубическая сингония (a = b = c; a = b = g = 90°), включающая решетки нескольких типов:
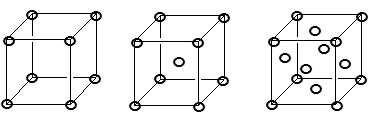
Примитивная Объемноцентрированная Гранецентрированная
В зависимости от природы химической связи между частицами различают ковалентные, ионные, металлические и молекулярные кристаллы.
Промежуточным между жидким и кристаллическим является жидкокристаллическое состояние вещества, для которого характерно наличие дальнего порядка в расположении частиц, способных свободно перемещаться друг относительно друга. Жидкокристаллическое (мезоморфное) состояние могут образовывать вещества, которые имеют вытянутые асимметричные молекулы, например, пара-азоксианизол:
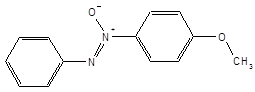

При плавлении вещества данного типа, молекулы ориентируются параллельно с образование мезоморфной фазы. При этом, с одной стороны, наблюдается дальний порядок расположения частиц и анизотропия свойств, характерные для кристалла. С другой стороны, возможна подвижность частиц, обусловливающая текучесть, характерную для жидкости.
Литература: [1] с. 143 - 158, 513 - 519; [2] с. 133 - 161; [3] с. 90 - 96
Лекция № 7. Основы химической термодинамики. Термохимические расчеты
Химическая термодинамика – это раздел физической химии, изучающий энергетические эффекты и направленность химических процессов. Предметом изучения термодинамики является термодинамическая система - тело или совокупность тел в объеме, ограниченном от окружающей среды реальными или условными перегородками. Выделяют три типа термодинамических систем:
ü изолированные, которые не обмениваются с окружающей средой ни массой, ни энергией;
ü закрытые, которые обмениваются с окружающей средой энергией, но не обмениваются массой;
ü открытые, для которых возможен свободный массо- и энергообмен с окружающей средой.
По фазовому составу различают гомогенные и гетерогенные системы. Гомогенные системы состоят из одной фазы, гетерогенные включают несколько фаз. Фаза - это совокупность однородных частей системы, обладающих одинаковыми свойствами во всех ее точках, ограниченная от других частей системы поверхностью раздела.
Состояние системы описывается рядом параметров: химическим составом, температурой, давлением, объемом, массой, количеством вещества. Кроме этого для описания системы и происходящих в ней изменений (термодинамических процессов) применяется ряд термодинамических функций: внутренняя энергия, энтальпия, энтропия, изобарно-изотермический потенциал (свободная энергия Гиббса).
Внутренняя энергия(U) - это совокупность всех видов энергии термодинамической системы за исключением кинетической энергии ее движения как целого и потенциальной энергии ее положения в каком-либо внешнем поле. Поскольку во внутреннюю энергию входят все виды энергии, заключенные в материи, даже те, которые нам еще неизвестны, абсолютное ее значение не подлежит определению. Тем не менее, можно определить изменение внутренней энергии в результате какого-либо процесса (DU = U2 - U1). При этом величина изменения внутренней энергии не зависит от пути проведения процесса, а определяется только конечным и начальным состоянием системы, т.е. внутренняя энергия является функцией состояния:
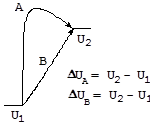
В термодинамике различают два вида процессов: изохорный, проводимый при постоянном объеме, и изобарный, проводимый при постоянном давлении. Тепло, сообщенное системе в изохорном процессе, идет на увеличение ее внутренней энергии: QV = DU.
Тепло, сообщенное системе в изобарном процессе, идет на увеличение ее внутренней энергии и совершение работы против сил внешнего воздействия: Qp = DU + A. Последнее выражение представляет собой одну из формулировок первого начала термодинамики. Поскольку при сообщении тепла при постоянном давлении система расширяется, она совершает работу против силы внешнего давления: A = pDV. Подставим эту формулу в математическое выражение первого начала термодинамики и сгруппируем переменные:
Qp = DU + pDV = U2 - U1 + p(V2 - V1) = (U2 + pV2) - (U1 + pV1) = H2 - H1 = DH
Из полученного выражения следует, что тепло, сообщенное системе при изобарном процессе, идет на увеличение функции H = U + pV. Эта функция получила название - энтальпия. Следует отметить, что, так же как и внутренняя энергия, энтальпия является функцией состояния и ее изменение не зависит от пути проведения процесса, а определяется конечным и начальным состоянием системы. Поскольку в выражение энтальпии входит внутренняя энергия, абсолютное ее значение также неопределимо.
Энтальпия широко используется в термохимических расчетах, целью которых является определение теплового эффекта химической реакции, проводимой обычно при постоянном давлении. Выполняются расчеты на основании термохимических уравнений, которые заметно отличаются от химических уравнений реакций. Например, термохимическое уравнение реакции образования воды будет выглядеть следующим образом:
H2(г) + 1/2O2(г) = H2O(ж); DH°298 = -285,83 кДж
Отличия от обычного уравнения химической реакции (2H2 + O2 = 2H2О) заключаются в следующем:
· Коэффициенты в термохимическом уравнении указывают на количество вещества, поэтому могут быть дробными и обычно подбираются таким образом, чтобы целевой продукт реакции имел коэффициент, равный единице.
· Указывается тепловой эффект в виде изменения энтальпии (DH).Следует обратить внимание на то, что процесс рассматривается со стороны термодинамической системы, поэтому для экзотермических реакций DH имеет отрицательное значение, а для эндотермических - положительное.
· Обязательно указывается агрегатное состояние реагентов и продуктов реакции, поскольку изменение агрегатного состояния (фазовый переход) требует энергетических затрат и влечет за собой изменение теплового эффекта, например,
H2(г) + 1/2O2(г) = H2O(ж); DH°298 = -285,83 кДж
H2(г) + 1/2O2(г) = H2O(г); DH°298 = -241,82 кДж
Одной из фундаментальных термодинамических характеристик вещества является стандартная энтальпия образования (DH0f)- изменение энтальпии в процессе образования одного моля вещества из простых веществ в стандартных условиях. Стандартному состоянию в термодинамике отвечает температура 298 К (25 °С) и давление 101,325 кПа (1 атм.). Из определения следует, что энтальпия образования простого вещества, наиболее устойчивого в стандартных условиях, равна нулю. Найти величины стандартных энтальпий образования многих веществ можно в соответствующих справочниках.
В основе термохимических расчетов лежит закон Гесса (Г.И. Гесс, 1841) - тепловой эффект химической реакции не зависит от пути проведения процесса и числа его промежуточных стадий, а определяется начальным и конечным состоянием системы. Конкретные расчеты выполняют на основании следствий из закона Гесса.
Следствие первое - с термохимическими реакциями можно выполнять арифметические операции. Таким образом, комбинируя термохимические уравнения, можно определять тепловые эффекты в принципе любых реакций, в том числе и тех, для которых его определение связано с экспериментальными сложностями или вообще невыполнимо. Например, невозможно экспериментально определить тепловой эффект реакции образования оксида углерода(II):
С(графит) + 1/2О2(г) = СО(г),
поскольку большое сродство углерода к кислороду приводит к образованию примеси СО2 даже при недостатке кислорода. В то же время легко поддаются экспериментальному определению тепловые эффекты следующих реакций:
С(графит) + О2(г) = СО2(г); DH1 = -393,5 кДж
СO(г) + 1/2O2(г) = CO2(г); DH2 = -283 кДж
Вычтя второе уравнение из первого, получим уравнение образования оксида углерода(II):
С(графит) + О2(г) - СO(г) + 1/2O2(г) = СО2(г) - СО2(г)
С(графит) - СO(г) + 1/2O2(г) = 0
С(графит) + 1/2O2(г) = СO(г)
Соответствующая комбинация тепловых эффектов реакций дает искомый тепловой эффект
DH = DH1 - DH2 = -393,5 - (-283) = -110,5 (кДж)
Следствие второе - тепловой эффект химической реакции равен разности суммы энтальпий образования продуктов реакции и суммы энтальпий образования исходных веществ (реагентов).
DH0298 = 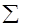 iDH0f(пр) -
iDH0f(пр) - 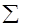 jDH0f(реаг)
jDH0f(реаг)
Применение данного следствия позволяет рассчитать тепловой эффект любой реакции, для которой известны стандартные энтальпии образования реагентов и продуктов реакции (справочные данные).
Рассчитаем в качестве примера тепловой эффект реакции термического разложения карбоната кальция:
CaCO3(к) = CaO(к) + CO2(г)
DH0298 = DH0f(CaO) + DH0f(CO2) - DH0f(CaCO3)
DH0298 = -635,5 + (-393,5) - (-1206,9) = 177,9 кДж
Следствие третье - тепловой эффект химической реакции равен разности суммы энтальпий сгорания исходных веществ и суммы энтальпий сгорания продуктов реакции.
DH0298 = 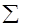 iDH0сгор(реаг) -
iDH0сгор(реаг) - 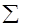 jDH0сгор(пр)
jDH0сгор(пр)
В качестве примера рассчитаем энтальпию процесса перехода цис-бутена-2 в транс-изомер.
cis-С4Н8 = trans-C4H8
DH0298 = DH0сгор(cis-C4H8) - DH0сгор(trans-C4H8); DH0298 = -2710,4 - (-2706,2) = -4,2 кДж
В основе химических процессов, наряду со стремлением к минимуму энергии, отчетливо проявляется тенденция системы к переходу в состояние с максимальной неупорядоченностью расположения частиц. Для отражения этой тенденции в термодинамике существует специальная функция - энтропия (S), которая определяется уравнением Больцмана:
S = RlnW,
где W - термодинамическая вероятность системы.
Термодинамической вероятностью называется число микросостояний системы (способов расположения ее частиц), отвечающее данному ее макросостоянию. Рассмотрим в качестве модельной системы, распределение четырех молекул газа по двум половинам сосуда.
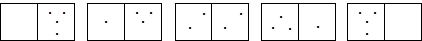
W = 1 W = 4 W = 6 W = 4 W = 1
Первое состояние можно реализовать только одним способом. Второе состояние можно реализовать четырьмя способами, меняя молекулу в левой части системы. При реализации третьего состояния возможны шесть перестановок молекул, поэтому вероятность данного состояния равна шести. Очевидно, что термодинамическая вероятность, а соответственно и энтропия состояния, отвечающего равномерному распределению молекул в системе максимальна. Стремление системы перейти в состояние с максимальной неупорядоченностью отражает второе начало термодинамики - процессы, не сопровождающиеся энергетическими эффектами, самопроизвольно идут в сторону увеличения энтропии.
Следует отметить, что, в отличие от внутренней энергии и энтальпии, энтропия может быть рассчитана методами статистической термодинамики. Изменение энтропии в результате какого-либо процесса можно рассчитать по второму следствию закона Гесса, поскольку энтропия является функцией состояния системы. Можно определить изменение энтропии и экспериментально, зная количественно тепла, переданного в изотермическом процессе:
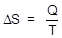 ,
,
где Q - теплота, которой система обменивается с внешней средой при постоянной температуре Т.
Как уже отмечалось, в основе химических реакций лежат две противоположно направленные тенденции:
· стремление частиц к соединению с образованием химических связей и выделением энергии;
· стремление атомов к разрыву химических связей и увеличению энтропии.
Попытаемся определить, какая из тенденций будет превалировать в тех или иных условиях. Для этого перепишем уравнение первого начала термодинамики, разделив работу на работу расширения - pDV и полезную работу - Апол
DU = Qp - Aпол - pDV
Поскольку DH = DU + pDV, а DU = DH - pDV данное уравнение можно преобразовать к следующему виду:
DH = Q - Aпол
Так как DS = Q/T, а Q = TDS, то
DH = ТDS - Aпол
Aпол = -(DH - ТDS)
Это значит, что в системе может совершаться работа химического процесса, т.е. он может идти самопроизвольно, только в том случае, когда DH - ТDS < 0. Комбинация термодинамических функций сама является функцией состояния, которая получила названиесвободная энергия Гиббса (G) или изобарно-изотермический потенциал G = H - ТS.
Величина изменения свободной энергии Гиббса позволяет решить вопрос о принципиальной возможности химической реакции:
DG < 0 - реакция принципиально осуществима;
DG > 0 - реакция принципиально не осуществима;
DG = 0 - система находится в состоянии химического равновесия.
Аналогично энтальпии образования в термодинамике широко используется энергия Гиббса образования (DGf0), как изменение свободной энергии Гиббса в процессе образования одного моля вещества из простых веществ в стандартных условиях. Энергии Гиббса образования - табличные величины, на основании которых по закону Гесса можно рассчитать DG для той или иной реакции:
DG0298 = 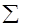 iDGf0(пр) -
iDGf0(пр) - 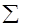 jDGf0(реаг)
jDGf0(реаг)
Литература: [1] с. 158 - 157, 182 - 196; [2] с. 162 - 195; [3] с. 155 - 174
Лекция № 8. Основные положения химической кинетики. Катализ и катализаторы.
Дата добавления: 2017-10-04; просмотров: 2329;











