В реальных гидроакустических приборах принятые допущения учитывают вводом поправочных коэффициентов.

Простейшим типом акустической волны является плоская волна (волна, распространяющаяся только в одном направлении):

.

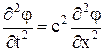Волновое уравнение плоской волны для функции смещения частиц жидкости:

.

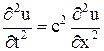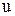- амплитуда смещения частиц.

Частным случаем плоской волны является гармоническая плоская волна, волновое уравнение которой имеет следующий вид:

,

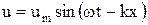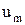- амплитудное значение смещения частиц;

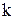- волновое число ( ).

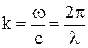Колебательная скорость частиц:

,

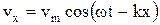где .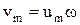

Акустическое давление такой волны имеет следующий вид:

,

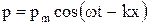Где .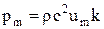

Звуковая волна при своем распространении сообщает частицам среды кинетическую энергию и изменяет их потенциальную. Интенсивность плоской гармонической волны можно определить следующим образом:

.

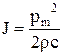Таким образом, при одинаковых амплитудах акустического давления в двух средах с различными плотностями 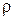, интенсивность колебаний будет больше в менее плотной среде.

Скорость распространения акустических волн в водной среде играет важную роль в гидролокации, так как входит в расчетную форму для определения расстояния до подводного объекта.

,

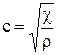где 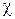- модуль объемной упругости.

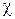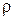Величины и являются функциями температуры, солености и гидростатического давления.

Количественную оценку изменения скорости звука с расстоянием дает градиент скорости, равный изменению скорости на единицу расстояния. Для судовождения практическое значение имеет лишь вертикальный градиент скорости звука в воде. Он считается положительным если с увеличением глубины скорость звука растет, и отрицательным, если уменьшается.