Относительного движения МТ

Дифференциальные уравнения

Пусть имеется инерциальная система отсчета О₁x₁y₁z₁. Рассмотрим движение МТ массы m по отношению к неинерциальной системе отсчета Oxyz, которая произвольным образом (с ускорением) движется по отношению к инерциальной системе отсчета (рис. 18).

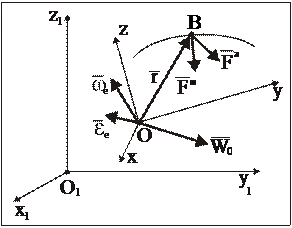
Рис. 18

На основании второго (основного) закона динамики – соотношения (1.2) для несвободной МТ имеем:

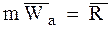, (2.1)

где 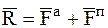, 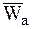– абсолютное ускорение МТ – ускорение МТ по отношению к инерциальной системе координат.

Используя теорему о сложении скоростей в сложном движении МТ (Ч.1 Кинематика), перепишем соотношение (2.1) в виде:

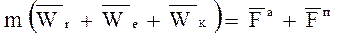, (2.2)

здесь 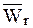– относительное ускорение МТ, 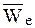– переносное ускорение МТ, 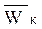– ускорение Кориолиса.

Совершив простейшие алгебраические преобразования и введя обозначения сил инерции, получим дифференциальное уравнение относительного движения МТ:

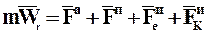, (2.3)

где 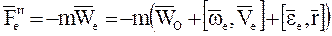– переносная сила инерции,

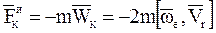– сила инерции Кориолиса.

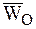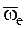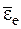В этих соотношениях использованы формулы (Ч.1 Кинематика) для ускорения точки НМС в общем случае ее движения и формулы для ускорения Кориолиса, в которых – абсолютное ускорение начала неинерциальной системы координат, и – угловые скорость и ускорение неинерциальной системы координат по отношению к инерциально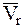й, и 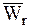– относительные скорость и ускорения МТ по отношению неинерциальной системы координат.

Из соотношения (2.3) следует, что движение МТ относительно неинерциальной системы отсчета можно рассматривать так же, как и относительно инерциальной, добавляя при этом в правую часть уравнения движения МТ переносную и кориолисову силы инерции.